ТОЭ. Определение тока, потенциала, напряжения

• Название: Определение тока, потенциала, напряжения
• Дата: 13.10.2021
• Размер: 0.64 Mb.
• Имя файла: ТОЭ.doc
• Тип: Документы; #247114
• страница: 1 из 3

1. 
   Определение тока, потенциала , напряжения
   

Явление направленного движения свободных носителей электрических зарядов в проводящей среде называется электрическим током.

Численно ток определяется как предел отношения количества электричества , переносимого заряженными частицами через поперечное сечение проводника за интервал времени , к величине , когда последний стремится к нулю

.

Сопротивление:
Пусть через участок цепи с сопротивлением r проходит ток i.



Разность электрических потенциалов точек 1 и 2 представляет собой напряжение на данном участке (сопротивлении):

.

Численно напряжение равно работе, совершаемой силами электрического поля по перемещению единичного положительного заряда из точки 1 в точку 2.

2. 
   Источники ЭДС и тока
   

В теории электрических цепей пользуются идеализированными источниками электрической энергии: источником ЭДС и источником тока. Им приписывают следующие свойства.

Идеальным источником ЭДС называется активный элемент с двумя выводами (рис. 1.9), напряжение на которых не зависит от величины тока, проходящего через источник. Внутреннее сопротивление идеального источника ЭДС равно нулю.

Упорядоченное перемещение положительных зарядов внутри источника от клеммы « – » к клемме « + » происходит за счет присущих источнику сторонних сил. Величина, численно равная работе, совершаемой сторонними силами при перемещении единичного положительного заряда от зажима « – » к зажиму « + », называется ЭДС источника и обозначается Е.

Рис. 1.9
При подключении нагрузки (сопротивление r, рис. 1.10) к источнику возникает замкнутый путь для протекания тока, который направлен вне источника от клеммы « + » к клемме « – ».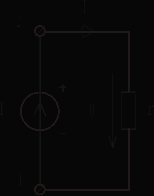


Рис. 1.10
Идеальным источником тока называется активный элемент с двумя выводами (рис. 1.13), ток которого J не зависит от напряжения на его зажимах. Внутреннее сопротивление идеального источника тока бесконечно велико.

При подключении нагрузки (сопротивление r, рис. 1.13) к источнику возникает замкнутый путь для протекания тока I. Указанные выше свойства источника тока приводят к тому, что ток в ветви, куда включен источник тока (в рассматриваемом случае – в одноконтурной цепи), всегда равен току самого источника: I = J.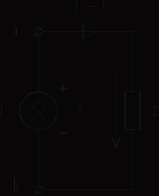


Рис. 1.13

3. 
   Закон Ома для участка цепи и ЭДС
   

Позволяет определить ток по известным величинам ЭДС и напряжения на концах этого участка.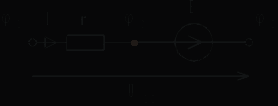


Рис. 1.17
Дано: .

Определить I.
Выразим потенциалы точек а и с рассматриваемого участка цепи рис. 1.17:

,

.

Тогда напряжение на зажимах а, с

.

Отсюда искомый ток

. (1.17)

Отметим, что в рассматриваемом случае (рис. 1.17) направление тока и источника ЭДС совпадают, что отражается знаком « + » перед ЭДС Е в формуле (1.17).

Если направление тока и источника ЭДС противоположны (рис. 1.18), то закон Ома принимает вид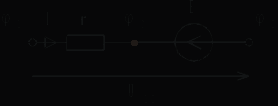

Рис. 1.18
. (1.18)

4. 
   Законы Кирхгофа
   

Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю
. (1.19)
При этом токам, направленным к узлу, приписывается какой-либо один знак (например « + »), а от узла – противоположный.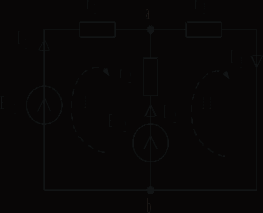

Рис. 1.19
Так, для узла а цепи рис. 1.19 первый закон Кирхгофа имеет вид:
.
Второй закон Кирхгофа: алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений на остальных элементах этого контура:

. (1.20)
Предварительно необходимо произвольно выбрать направление обхода контура, например, по часовой стрелке (см. рис. 1.19). Если направления ЭДС и условные положительные направления напряжений на элементах контура совпадают с выбранным направлением обхода контура, то такие ЭДС и напряжения записываются со знаком « + », в противном случае - « - ».

5. 
   Принцип наложения
   

Принцип наложения: ток в любой ветви электрической цепи равен алгебраической сумме токов, вызываемых каждым источником электрической энергии в отдельности. Этот принцип справедлив для всех линейных электрических цепей.

Принцип наложения применяется в методе расчета, получившем название метода наложения. При использовании данного метода поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждого источника электрической энергии в отдельности, мысленно удаляя остальные источники из схемы. При этом внутренние сопротивления источников должны остаться в цепи. Это означает, что участок ветви, в котором был источник ЭДС, замыкается накоротко (рис. 4.16а), а участок с источником тока размыкается (рис. 4.16б). Затем находят фактические токи в ветвях путем алгебраического сложения частичных токов. Если направление частичного тока совпадает с выбранным направлением фактического тока, то при суммировании частичный ток берется со знаком “ + ”, иначе “ - ”.

6. 
   Амплитуда, частота, начальная фаза синусоидально изменяющегося тока, напряжения, ЭДС
   

Обозначения мгновенных значений синусоидальных ЭДС, напряжения и тока являются однотипными: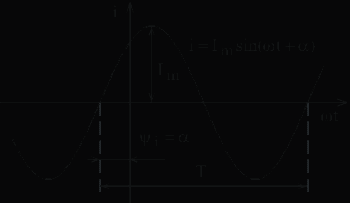

, (2.1)

, (2.2)

, (2.3)

где - амплитуда тока (рис. 2.1);
- угловая частота. Размерность .



Рис. 2.1
Аргумент, стоящий под знаком синуса , называется фазой. Она характеризует состояние колебания (то есть его численное значение) в любой момент времени.

Значение фазы в момент времени t = 0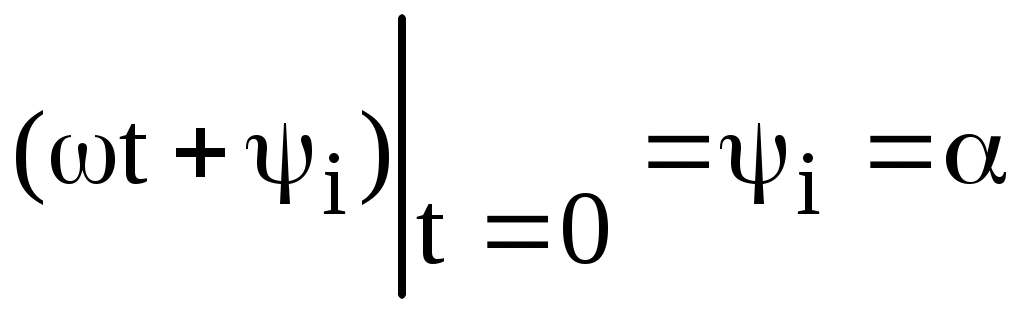



называется начальной фазой. Она характеризует состояние колебания (то есть его численное значение) при t = 0. Для обозначения начальных фаз напряжения и тока часто используют буквы и .
Частота тока f показывает, сколько полных колебаний происходит за одну секунду. Величины f и связаны соотношением

,

где f – частота, Гц.

7. 
   Действующие и средние значения синусоидально изменяющихся токов, напряжений ,ЭДС
   

Средним значением за период Т любой периодической функции называется величина

. (2.5)

В случае синусоидальной функции среднее значение за период равно нулю, так как площадь положительной полуволны компенсируется площадью отрицательной. В этом случае пользуются средним значением за полупериод: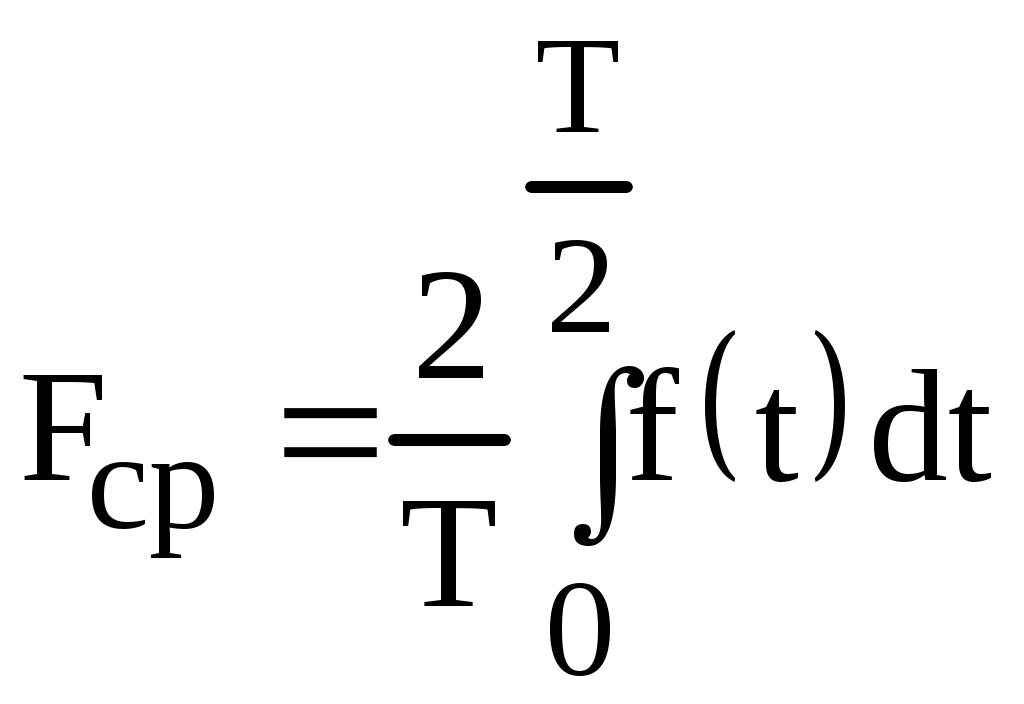

. (2.6)
Среднее значение за полупериод показывают электроизмерительные приборы выпрямительной системы.

Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым течет один и тот же ток, пропорциональны квадрату тока. Поэтому о величине переменного тока судят по так называемому действующему (среднеквадратичному) значению за период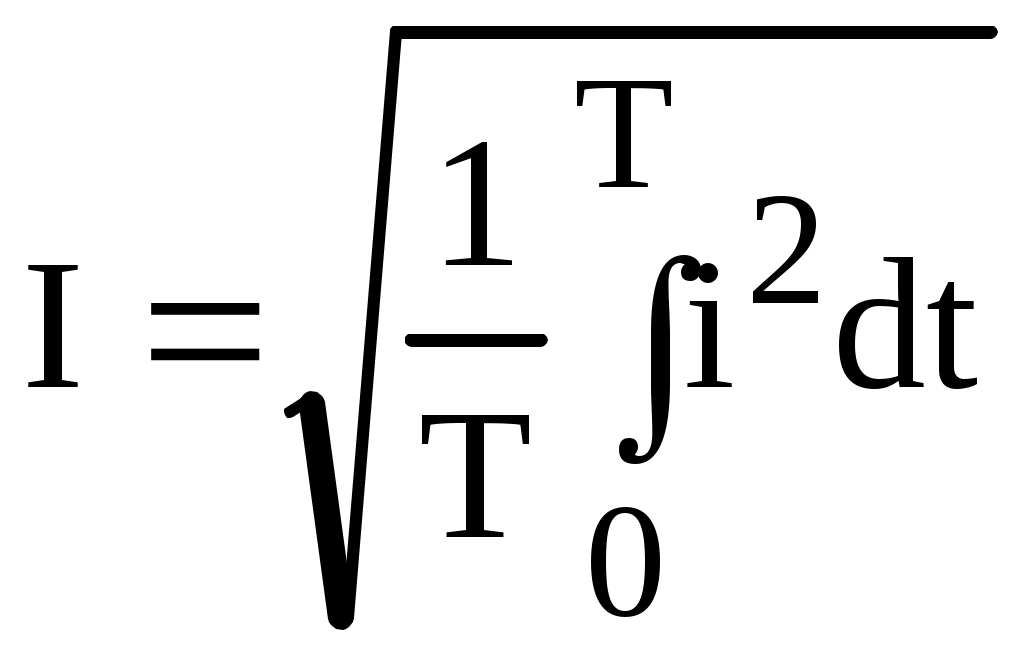

. (2.9)

8. 
   Мгновенная, активная, реактивная и полная мощности
   

Мгновенная мощность, поступающая в двухполюсник:
. (2.60)
График мгновенной мощности приведен на рис. 2.18. На интервале I, когда напряжение u и ток i имеют разные знаки, энергия возвращается из двухполюсника в источник ЭДС. На интервале II, когда напряжение и ток имеют одинаковые знаки, энергия направлена из источника в двухполюсник. Процесс обмена энергией между источником и приемником обусловлен наличием реактивных элементов в пассивном двухполюснике.

Активная мощность, рассеиваемая в двухполюснике:
. (2.61)
Раскрывая (2.61), получим
. (2.62)
Множитель называется коэффициентом мощности. Как было показано выше, активная мощность может быть только положительной. Следовательно, коэффициент мощности также всегда больше нуля и
. (2.63)
Величина

(2.64)
называется полной мощностью. Она соответствует той максимальной активной мощности, которая может быть получена в цепи при заданных действующих значениях напряжения U и тока I. Размерность полной мощности [S] = ВА.

Любая электрическая установка (например, трансформатор, двигатель) проектируетcя и изготавливается на полную мощность S. Однако из-за наличия угла сдвига фаз между напряжением и током расчетная мощность установки S используется не полностью. Отсюда ясна важность высокого значения коэффициента мощности .

Величина

(2.65)
называется реактивной мощностью. Реактивная мощность характеризует скорость передачи электрической энергии от источника энергии к приемнику и обратно.

Реактивная мощность положительна при отстающем токе и отрицательна при опережающем токе .

Размерность реактивной мощности [Q] = ВАp.

9. 
   Индуктивное и ёмкостное сопротивление
   

- реактивное сопротивление индуктивности;

- реактивная проводимость индуктивности.

- реактивное сопротивление емкости;

- реактивная проводимость емкости.

10. 
    Синусоидальный ток в емкости
    

Пусть к емкости С приложено синусоидальное напряжение (рис. 2.9)

. (2.25)

Ток в емкости

. (2.26)

Иначе:

. (2.27)

Рис. 2.8
Сопоставление полученного выражения для тока (2.26) и формулы (2.25) показывает, что ток в емкости опережает напряжение на угол

11. 
    Синусоидальный ток в индуктивности
    

Пусть через индуктивность L (рис. 2.6) течет синусоидальный ток (рис. 2.7)

. (2.17)

Рис. 2.6
Напряжение на индуктивности

. (2.18)

Иначе:

. (2.19)
Сопоставление полученного выражения для напряжения (2.18) и формулы (2.17) показывает, что напряжение на индуктивности опережает ток на угол

12. 
    Полное сопротивление и комплексное сопротивление двухполюсника
    

Отметим, что реактивное сопротивление индуктивности и реактивное сопротивление емкости всегда положительны, а входное реактивное сопротивление цепи может быть как положительным, так и отрицательным. Если x > 0, то угол сдвига фаз положителен и входное напряжение опережает ток. Говорят: ”Цепь имеет активно-индуктивный характер”. Если x < 0, то угол сдвига фаз отрицателен и входное напряжение отстает от тока. Говорят: ”Цепь имеет активно-емкостный характер”.

Обозначим
- (2.41)
где - полное сопротивление цепи.

Выражение (2.41) позволяет построить так называемый треугольник сопротивлений (рис. 2.11).

Рис. 2.11
. (3.23)
- входное комплексное сопротивление цепи

Перепишем в показательной форме записи:
. (3.25)