ТОЭ. Определение тока, потенциала, напряжения
 Скачать 0.64 Mb.
|
|
Законы Ома и Кирхгофа в комплексной форме г) комплексная амплитуда напряжения на сопротивлении  ; (3.19)д) комплексная амплитуда напряжения на индуктивности  ; (3.20)е) комплексная амплитуда напряжения на емкости  . (3.21)Формулы (3.19) – (3.21) представляют собой закон Ома в комплексной форме записи для отдельных пассивных элементов цепи. Перепишем (3.15) с учетом принятых обозначений:  . (3.22)Составим в качестве примера уравнения по законам Кирхгофа для цепи рис. 3.5.  Рис. 3.5 Отметим, что в качестве обозначений в схеме рис. 3.5 использованы комплексные действующие значения ЭДС и токов. Направления последних выбраны произвольно. Первый закон Кирхгофа для узла а:  .Для составления уравнений по второму закону Кирхгофа произвольно выбираем независимые контуры и направления их обхода (см. рис. 3.5). Сами уравнения имеют вид  , .Векторная диаграмма Векторной диаграммой называется совокупность векторов на комплексной плоскости, изображающих синусоидальные функции времени одинаковой частоты и построенных с соблюдением их взаимной ориентации по фазе. Баланс мощностей в цепи переменного тока Пусть источник ЭДС  нагружен на сопротивление  (рис. 3.25). Рис. 3.25 Известна величина тока в цепи  . Рассмотрим так называемый сопряженный комплекс тока  , аргумент которого (начальная фаза) имеет противоположный знак по сравнению с аргументом исходного тока  .Обозначим  - комплексная мощность источника. Раскроем последнее выражение: (3.27)Таким образом, активная мощность источника равна действительной части комплексной мощности  , а реактивная мощность – мнимой части  .Активная мощность приемников может быть записана с использованием комплексных действующих значений токов и комплексных сопротивлений как  , а реактивная мощность -  .Математически баланс активных и реактивных мощностей в комплексной форме можно представить одним выражением. Так, для цепи с источниками ЭДС и тока оно имеет вид  ,или  . (3.28) Рис. 3.26 Составим для цепи рис. 3.26 баланс мощностей в комплексной форме: 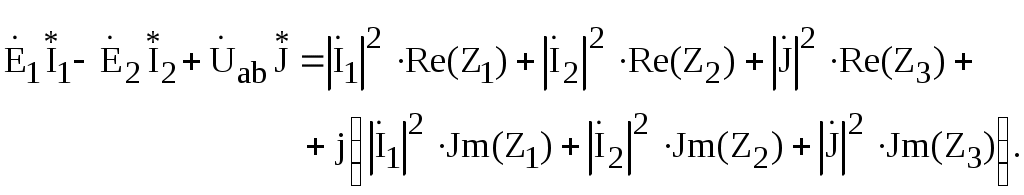 Общее условие возникновения резонанса напряжений. Резонанс напряжений может возникать в цепях с последовательным соединением участков, содержащих индуктивности и емкости. Примеры таких цепей приведены на рис. 6.2.  а)  б) Рис. 6.2 Общее условие возникновения резонанса напряжений – равенство нулю входного реактивного сопротивления цепи. Общее условие возникновения резонанса токов Резонанс токов может возникать в цепях с параллельным соединением участков, содержащих индуктивности и емкости. Примеры таких цепей приведены на рис. 6.11.  а) б) Рис. 6.11 Общее условие возникновения резонанса токов – равенство нулю входной реактивной проводимости цепи. Расчет напряжения смещения нейтрали в несимметричной трехфазной цепи «Звезда-Звезда» Несимметричный режим работы трехфазной цепи (при симметричном генераторе) обусловлен неравенством комплексных сопротивлений фаз нагрузки. В этом случае отдельные напряжения или токи трехфазной цепи не образуют симметричные системы, а в схеме “звезда – звезда без нулевого провода”, кроме того, появляется так называемое напряжение смещения нейтрали  (разность потенциалов между нулем генератора и нулем нагрузки). . (7.56)Системы прямой, обратной и нулевой последовательностей. Любая несимметричная трехфазная система токов, напряжений, ЭДС, магнитных потоков может быть представлена в виде суммы трех симметричных систем: прямой, обратной и нулевой последовательностей фаз. Условимся обозначать величины прямой последовательности индексом “1”, обратной - “2” и нулевой - “0”. Система прямой последовательности состоит из трех векторов 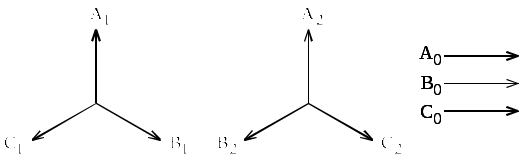 ,  ,  , равных по модулю и сдвинутых относительно друг друга на угол  , причем вектор отстает от вектора на угол (рис. 8.3 а). В системе обратной последовательности (рис. 8.3 б) вектор  опережает вектор  . Система нулевой последовательности образуется тремя одинаковыми векторами  (рис. 8.3 в). а) б) в) Рис. 8.3 Действующее значение периодического несинусоидального тока Действующее значение тока мы определяем как среднее квадратичное значение за период  Действующее значение периодического несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник  Коэффициент мощности  Коэффициент искажения:  Коэффициент формы кривой определяется как отношение действующего значения функции к среднему значению функции взятой по абсолютной величине: 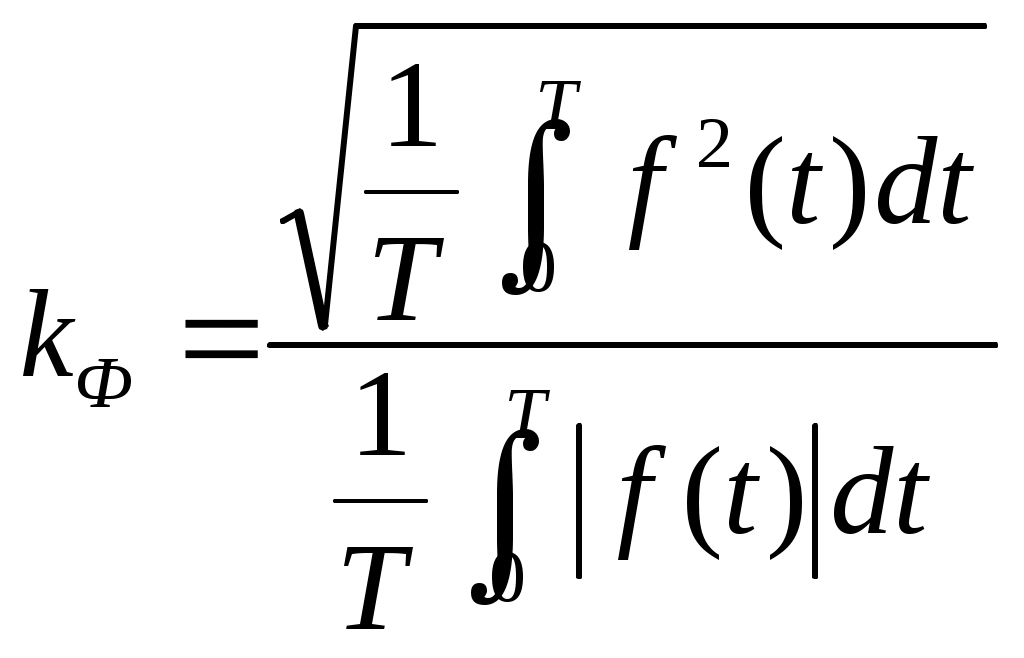 Коэффициент амплитуды определяется как отношение максимального значения функции к действующему её значению:  Определение четырехполюсника. Основные уравнения 4-хполюсника в А-форме В первой части были рассмотрены общие методы расчета электрических цепей: метод преобразований, метод контурных токов, узловых потенциалов и т. д. Однако, во многих случаях важно знать токи только некоторых ветвей и напряжения только между некоторыми узлами. В этом случае расчет цепи упрощается, если цепь разделить на отдельные части, каждая из которых соединяется двумя, тремя, зажимами с остальными частями. В различных областях электротехники, электросвязи, радиотехники особенно часто применяются аппараты и устройства с двумя парами зажимов, при помощи которых они соединяются с другими участками электрической цепи, т.е. четырехполюсники. Поэтому четырехполюсники выделены в отдельный раздел ТОЭ. На практике четырехполюсники и цепи, которые целесообразно представить состоящими из нескольких четырехполюсников, применяются, прежде всего, для передачи и преобразования электрических сигналов, несущих информацию. Тракт передачи информации или канал связи, как правило, состоит из четырехполюсников, включенных между генератором и приемником сигналов. В тракт передачи сигналов обычно входят: линия связи генератора и приемника, усилители, в которых увеличивается мощность, или, как говорят, уровень сигналов, фильтры, корректирующие контуры, трансформаторы и т.д. Условное изображение четырехполюсника показано на рис. 1 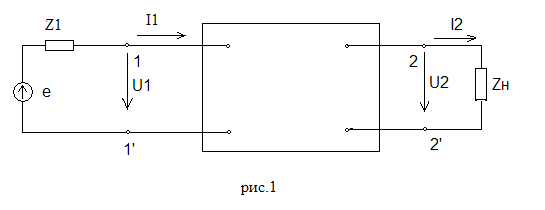 Уравнения типа А. Для исследования четырехполюсников необходимо прежде всего установить зависимость между четырьмя величинами определяющими режим его работы (U1, U2, I1, I2).(рис.1). Пусть положительные направления токов направления токов направлены от генератора в нагрузку. Первичные зажимы назовем входными, а вторичные – выходными. Цепь, представленная на рис.1 является линейной, у такой электрической цепи между тремя любыми напряжениями и токами существует линейная зависимость вида z = ax + by, где x, y, z – любые из токов и напряжений цепи. Выразим напряжение и ток на входе через напряжение и ток на выходе четырехполюсника: U1 = AU2 + BI2 I1 = CU2 + DI2 Эти уравнения, связывающие первичное напряжение U1 и I1 с вторичным напряжением U2 и током I2, называют основными уравнениями четырехполюсника, уравнениями передачи или системой уравнений типа А. Характеристическое сопротивление 4-хполюсника Довольно часто между источником питания и приемником включают симметричный четырехполюсник, например, наружная телевизионная антенна (генератор сигналов для телевизора) подсоединяется к телевизору не непосредственно, а при помощи симметричного четырехполюсника – телевизионного кабеля. Отрезок кабеля имеет два входных 1 – 1’ и два выходных 2 – 2’ зажима. Очень важно правильно выбрать сопротивление приемника Zn. Его подбирают так, чтобы входное сопротивление кабеля Z1вх было равным Zn, независимо от длины кабеля. При одинаковых входных сопротивлениях Z1вх кабелей разной длины, все генераторы – антенны будут одинаково нагруженными, что очень важно при их серийном изготовлении. Итак, если выбрать  , то и Z1вх = Zn. Входное сопротивление четырехполюсника при такой нагрузке зависит только от коэффициентов четырехполюсника (В и С) и, значит, может быть принято одним из параметров четырехполюсника. Новый параметр надо знать, если возникает задача о выборе нагрузки (Zn) для готового четырехполюсника или наоборот, если проектируют четырехполюсник для совместной работы с заданной нагрузкой.Параметр  обозначают через Zc и называют характеристическим сопротивлением симметричного четырехполюсника: Единицы измерения затухания 4-хполюсника Постоянная передачи – второй параметр симметричного четырехполюсника. Хотя постоянная передачи и выражена через напряжение и токи на входе и выходе четырехполюсника, но она полностью определяется структурой четырехполюсника и параметрами составляющих его элементов. Постоянную передачи можно, например, определить через коэффициенты A, B, C, D. По выражению  Характеристическое сопротивление и постоянную передачи называют вторичными параметрами четырехполюсника. 1дб = 0,115 Неп, 1 Неп = 8,7 дб. Отметим еще, что при вычислении постоянной передачи по формуле g = a + jb следует подставлять а в неперах, а b - в радианах. Законы коммутации и начальные условия В любой электрической цепи, в которой не могут развиваться бесконечно большие напряжения или протекать бесконечно большие токи, мгновенная мощность Р – величина всегда конечная, а потому в момент коммутации остаются неизменными напряжения на обкладках конденсатора и токи в индуктивных катушках  и  Независимые начальные условия  и  Служат для определения постоянных интегрирования  Постоянная времени электрической цепи Величина  имеет размерность времени и называется постоянной времени цепи. За промежуток  ток убывает в «е» раз.Переход от изображения к оригиналу с помощью теоремы разложения Теорема разложения позволяет перейти от изображения х(р) к оригиналу х(t)  Закон Кирхгофа для магнитной цепи Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю:  Второй закон Кирхгофа: алгебраическая сумма падений магнитного напряжения вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль того же контура:  Роль магнитных ферромагнитных материалов в магнитной цепи Все ферромагнитные материалы могут быть подразделены на две большие группы: магнитомягкие и магнитотвердые. Магнитомягкие материалы обладают круто поднимающейся основной кривой намагничивания и относительно малыми площадями гистерезисных петель. Наличие ферромагнитных материалов увеличивает поток в магнитной цепи. Кроме усиления магнитного потока, введение ферромагнитных материалов в цепь преследует также и другую цель: сосредоточение магнитного поля в определенной области пространства и придание ему определенной конфигурации |