ТОЭ. Определение тока, потенциала, напряжения
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Электрическая цепь с распределенными параметрами (длинные линии). Дифференциальные уравнения длинной линии В предыдущих главах рассматривались электрические цепи, которые называют цепями с сосредоточенными параметрами. При исследовании таких цепей считают, что электрическое поле сосредоточено в конденсаторах, эти участки были представлены на схемах с емкостями; магнитное поле сосредоточено в катушках индуктивности, в трансформаторах, эти участки на схемах обозначались индуктивностями; и, наконец, необратимые преобразования электромагнитной энергии в тепловую, химическую и механическую были представлены на схемах с сопротивлениями. В электротехнике, однако, часто встречаются электрические цепи, которые нельзя считать цепями с сосредоточенными параметрами. Эти цепи называют цепями с распределенными параметрами, так как электрическое поле, магнитное поле и потери энергии распределены равномерно или неравномерно вдоль всех участков цепи. В цепях с распределенными параметрами напряжения и токи различны не только на отдельных участках, но и изменяются в пределах каждого участка, т.е. зависят от пространственной координаты каждого участка. К цепям с распределенными параметрами относятся линии электропередач, линии телефонной и телеграфной связи, линии телеуправления и телеизмерения, антенны радиопередатчиков, обмотки трансформаторов и т.д. За точку начала отсчета выберем начало линии. Разность напряжений в начале и конце участка dxравна сумме падений напряжений на активном и индуктивном сопротивлениях. Изменение тока на участке равно сумме утечек тока через активную проводимость и емкость, т.е. Частные производные в этих уравнениях записаны потому, что u(x,t) и i(x,t)- зависят от двух координат. Или 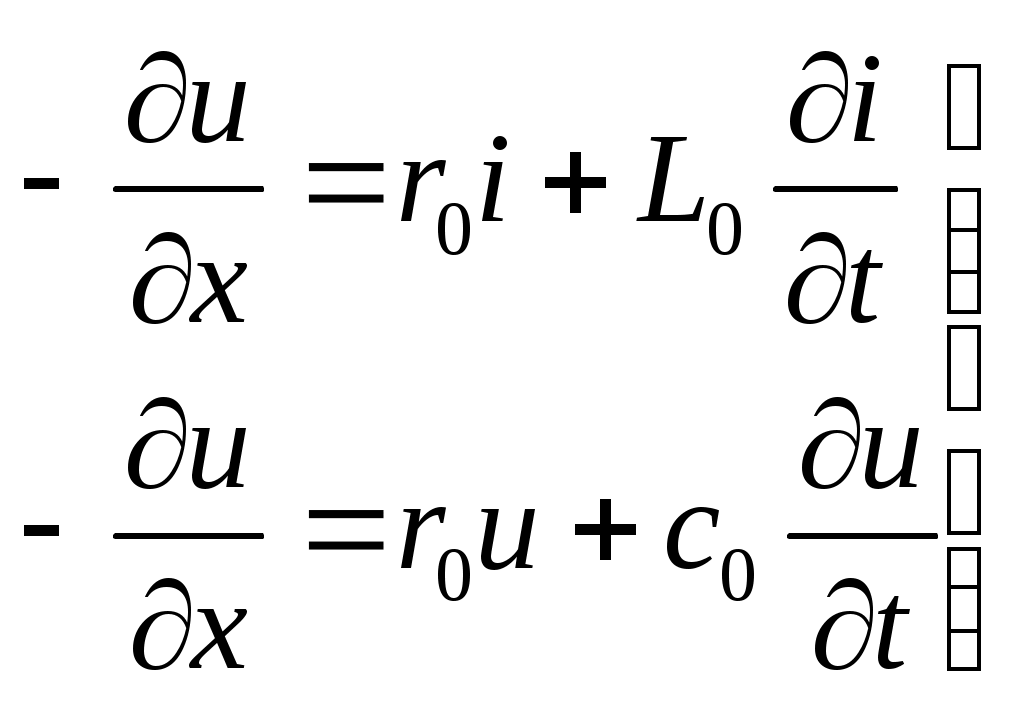 телеграфные уравнения длинных линий. телеграфные уравнения длинных линий.Скорость распространения волн токов и напряжений в длинной линии. Длина волны. Фазовая скорость при Прямая и обратная волны кроме фазовой скорости характеризуются еще длиной Длиной волны Длину волны Например, для воздушной линии электропередачи (f=50 Гц), считая Для воздушной линии, которая соединяет радиопередатчик, работающий на частоте f=30 МГц, с антенной, длина волны Наибольшая скорость движения волн получается в воздушной линии, где потерями можно пренебречь. В кабеле без потерь Волновое сопротивление и коэффициент распространения длинной линии Свойства линии как устройства для передачи энергии или информации вполне определяются двумя параметрами: коэффициентом передачи (распространения) Эти величины зависят от первичных параметров Величина Ее называют коэффициентом затухания. Величина [ Коэффициенты отражения по напряжению и току В однородной линии с генератором в начале и приемником в конце обратная, волна возникает, когда нагрузка не согласована: ZH Отношение комплексного напряжения (тока) обратной волны в конце линии 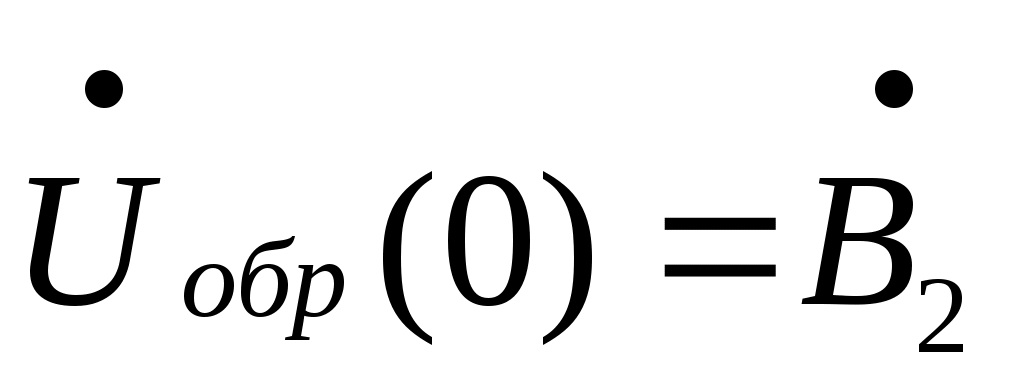 к комплексному напряжению (току) прямой волны к комплексному напряжению (току) прямой волны 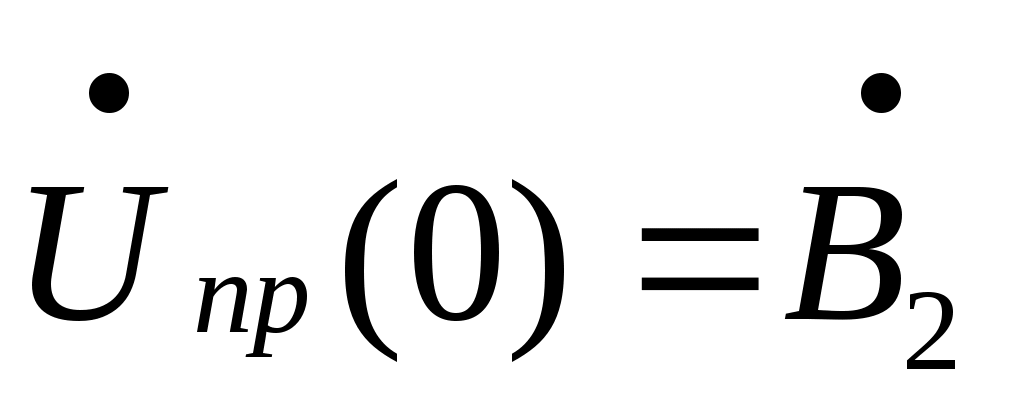 называют коэффициентом отражения: называют коэффициентом отражения: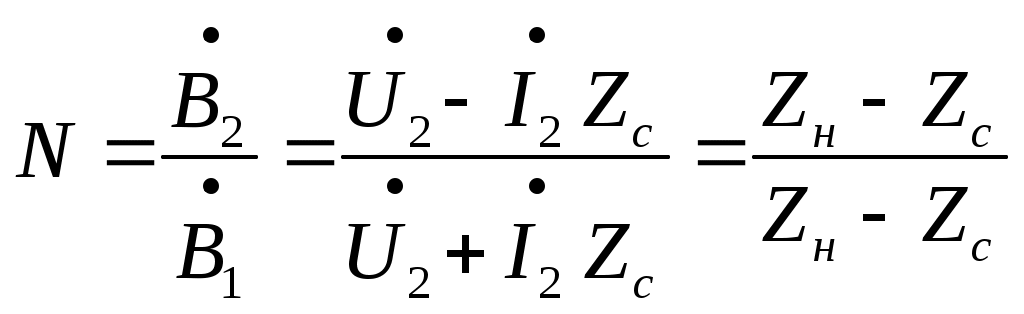 При коротком замыкании При холостом ходе Режим согласованной нагрузки длинной линии. КПД линии Линии передачи информации с генератором в начале линии и приемником в конце довольно часто работают в режиме согласованной нагрузки, т.е. при сопротивлении приемника, равном волновому сопротивлению линии: При согласованной нагрузке коэффициент 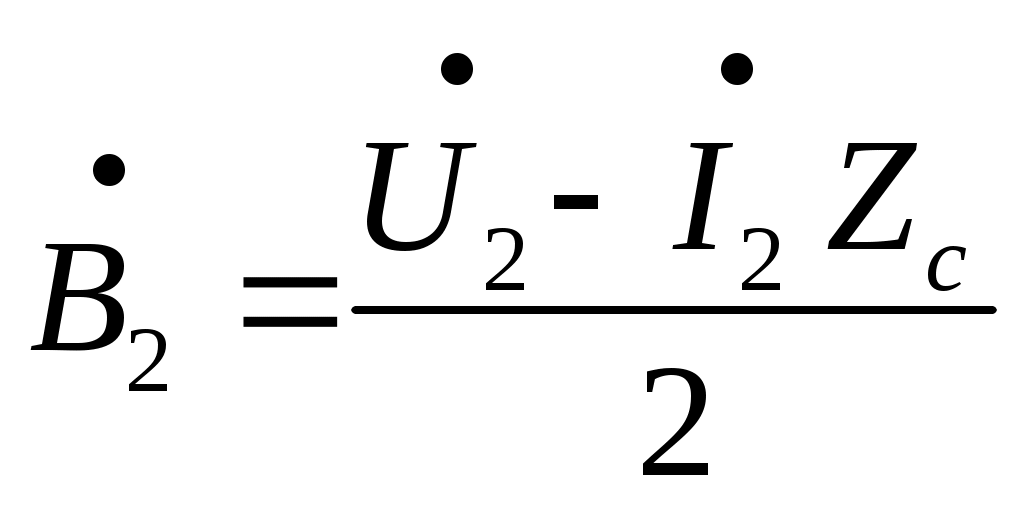 равен 0. равен 0.Следовательно, в линии отсутствует обратная волна 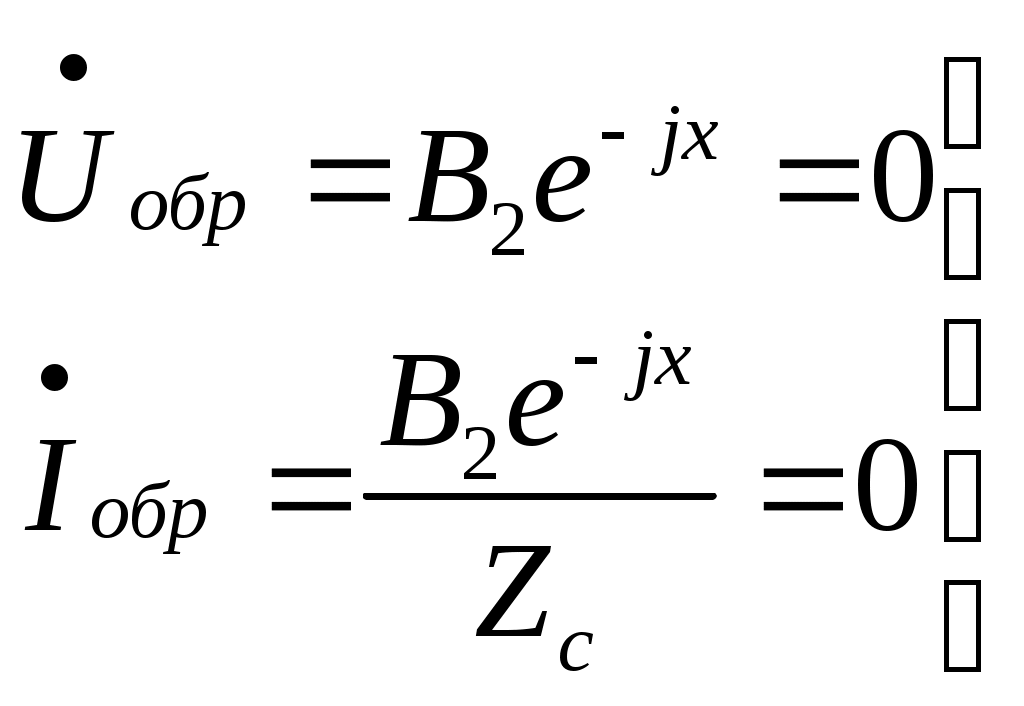 Уравнения линии значительно упрощаются: 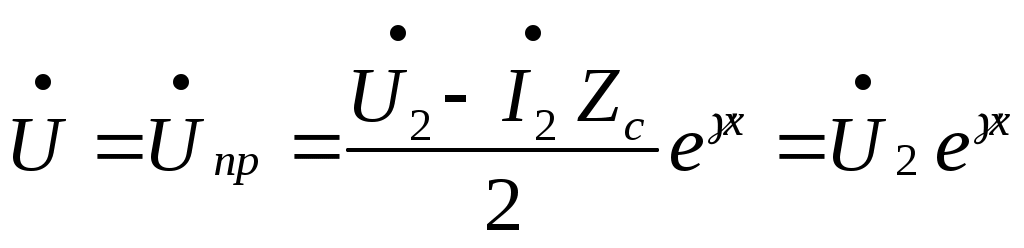 ; ;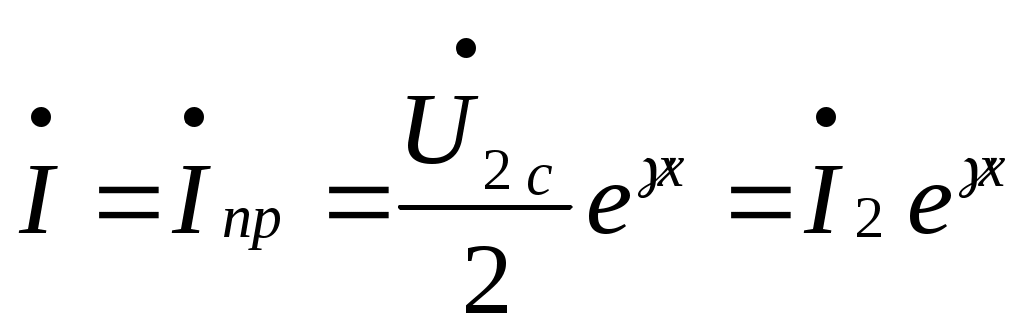 Действующее значение напряжения и тока из-за потерь в линии, не остаются юстоянными. Но закон изменения напряжения и тока очень прост: действующие значения напряжения тока постепенно уменьшаются к концу линии (рис. 4.6). 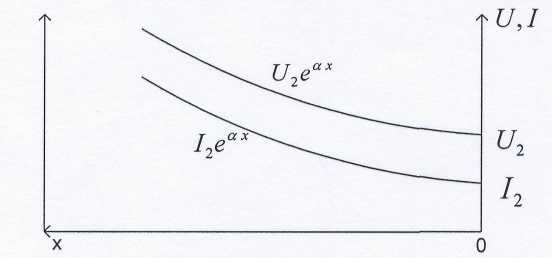 Рис. 4.6 КПД линии Связь напряженности и потенциала электростатического поля в интегральной и дифференциальной форме Потенциал произвольной точки поля может быть определен как работа, совершаемая силами поля по переносу единичного положительного заряда из данной точки поля в точку поля потенциал которой равен нулю.  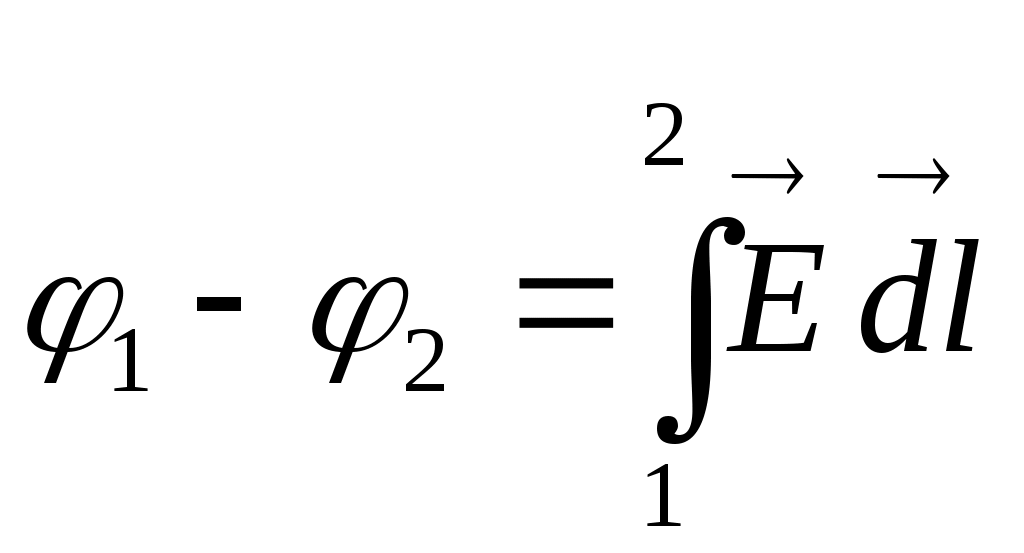 Теорема Гаусса в интегральной и дифференциальной форме Теорема Гаусса является одной из важнейших теорем электростатики. Она может быть сформулирована и записана тремя способами: Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности Так как Существует ещё одна форма записи теоремы Гаусса, отличающаяся от двух предыдущих Дело в том, что поток вектора Запись условия потенциальности электростатического поля в интегральной и дифференциальной форме Закон Ома в Дифференциальной форме Он устанавливает связь между плотностью тока в данной точке Первый закон Кирхгофа в интегральной и дифференциальной формах Сумму входящего в объем и выходящего из объема токов записывают так Первое уравнение Максвелла Первое уравнение Максвелла записывают следующим образом В правой части имеется две плотности тока: плотность тока проводимости Таким образом смысл первого уравнения Максвелла состоит в том, что всякое изменение напряженности электрического поля во времени ( Второе уравнение Максвелла Второе уравнение Максвелла записывают следующим образом Физический смысл его состоит в том, что всякое изменение магнитного поля во времени ( Объемная плотность энергии электромагнитного поля Теорема Умова-Пойнтинга Теорема Умова-Пойнтинга для мгновенных значение записывают следующим образом Левая часть – поток вектора Пойнтинка внутрь объема; |
