Лаба 5. Построение теоретических интегральной и дифференциальной функций распределения по учебной дисциплине Математика

• Название: Построение теоретических интегральной и дифференциальной функций распределения по учебной дисциплине Математика
• Дата: 07.03.2022
• Размер: 126.46 Kb.
• Имя файла: Лаба 5.docx
• Тип: Лабораторная работа; #386118

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Российский государственный геологоразведочный университет имени

Серго Орджоникидзе»

(МГРИ)

Факультет геологии и геофизики нефти и газа

Кафедра геологии и разведки месторождений углеводородов

ЛАБОРАТОРНАЯ РАБОТА № 5

По теме: «Построение теоретических интегральной и дифференциальной функций распределения»

по учебной дисциплине: «Математика»

Вариант 3

Выполнил: Гаджиев М.М.

Студент группы: НДР-20

Проверил: преподаватель Севостьянов Н. А.
Москва 2021

Введение

1. 
   Цель работы
   

Изучение функции Гаусса, проверка гипотезы о нормальном законе распределения, критерий Неймана-Пирсона, стратегии Неймана-Пирсона, предложенных из методических материалов и лабораторной работы №1.

1.1 Задача лабораторной работы

Вычисление функции Гаусса, гипотезы о нормальном законе распределения, критерий Неймана-Пирсона, стратегии Неймана-Пирсона.

1.2 Содержание.

Введение 2

1 Цель работы 2

1.2 Задача лабораторной работы 2

1.3 Содержание 3

2 Ход работы 4
2.1 Выполнение А…………………………………………………………………4
2.2 Выполнене Б…………………………………………………………………7
2.3 Выполнение В………………………………………………………………..10

Заключение 15

Список использованной литературы 16

2. 
   Ход работы
   2.1 Выполнение А
   

1. 
   Составляем таблицу
   

xi	ui	ф(ui)	f(xi)	Pi=hf(xi)	F(xj)
7,07	-1,97	0,06	0,03	0,04	0,02
8,57	-1,22	0,19	0,09	0,14	0,11
10,07	-0,47	0,36	0,18	0,27	0,32
11,57	0,28	0,38	0,19	0,29	0,61
13,07	1,03	0,24	0,12	0,18	0,85
14,57	1,78	0,08	0,04	0,06	0,96
16,07	2,53	0,02	0,01	0,01	0,99

2. 
   Вносим значения ф(ui)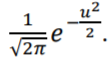
   

3. 
   С помощью полученных значений по формуле
   

где S – значение среднеквадратического отклонения.

4. 
   Вероятность попадания нормально распределенной случайной величины в i-тый интервал найдем по формуле:
   

Здесь h – интервал группирования. Для проверки правильности расчетов, вычислим сумму Pi.

5. 
   Для нахождения значений F(xj)воспользуемся встроенной функцией НОРМ.СТ.РАСП(z;интегральная)
   
6. 
   Для построения кривых теоретической и эмпирической интегральных функций распределения на одном графике выполним следующие шаги:
   

 скопируем из лабораторной работы №1 столбцы, содержащие правый край интервала группирования и значения эмпирической (наблюдаемой) функции.

 Добавим к скопированным столбец значений теоретической функции.

 Приведём график к стандартному виду, добавив координатные оси, подписи данных и т.д.

7. 
   Аналогично построим и сравним графики теоретической и эмпирической дифференциальных кривых распределения.
   
8. 
   Приводим графики к стандартному виду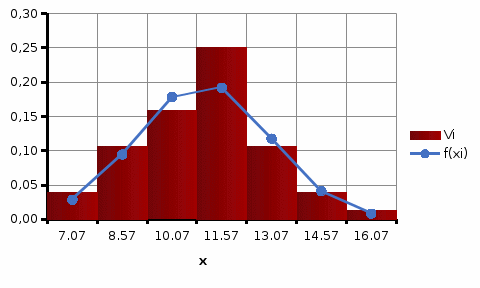
   

9. 
   Нашей задачей является сравнение эмпирических и теоретических 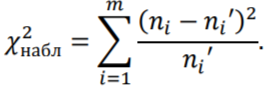частот по формуле.
   

10. 
    Составим вспомогательную таблицу из трех столбцов
    

ni	ni`=N*Pi	(ni-ni`)^2/ni`
3	2,311	0,206
8	7,656	0,015
12	14,452	0,416
19	15,546	0,768
8	9,528	0,245
3	3,327	0,032
1	0,662	0,173
54		1,855

Сумма и есть значение =1,855

Расхождение между статистическим и теоретическим распределениями является несущественным, если величина не превышает критического значения :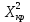



Вывод: Так как 1,855 то выдвинутую гипотезу о том, что случайная величина распределена по нормальному закону, можно с надежностью 1 – α = 0,95 считать правдоподобной, не противоречащей опытным данным.

2.2 Выполнение Б

1. 
   Составляем таблицу
   

xi	ui	ф(ui)	f(xi)	Pi=hf(xi)	F(xj)
8,65	-1,55	0,12	0,03	0,07	0,06
10,65	-0,98	0,25	0,07	0,14	0,16
12,65	-0,42	0,37	0,10	0,21	0,34
14,65	0,15	0,39	0,11	0,22	0,56
16,65	0,71	0,31	0,09	0,17	0,76
18,65	1,28	0,18	0,05	0,10	0,90
20,65	1,84	0,07	0,02	0,04	0,97

2. 
   Вносим значения ф(ui)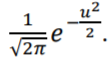
   

3. 
   С помощью полученных значений по формуле
   

где S – значение среднеквадратического отклонения.

4. 
   Вероятность попадания нормально распределенной случайной величины в i-тый интервал найдем по формуле:
   

Здесь h – интервал группирования. Для проверки правильности расчетов, вычислим сумму Pi.

5. 
   Для нахождения значений F(xj)воспользуемся встроенной функцией НОРМ.СТ.РАСП(z;интегральная)
   
6. 
   Для построения кривых теоретической и эмпирической интегральных функций распределения на одном графике выполним следующие шаги:
   

 скопируем из лабораторной работы №1 столбцы, содержащие правый край интервала группирования и значения эмпирической (наблюдаемой) функции.

 Добавим к скопированным столбец значений теоретической функции.

 Приведём график к стандартному виду, добавив координатные оси, подписи данных и т.д.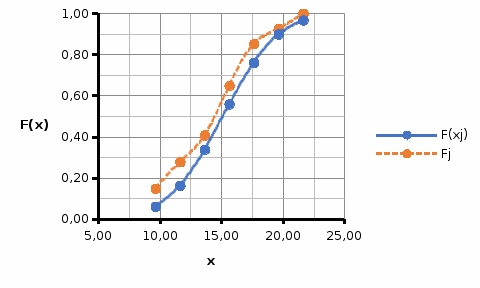

7. 
   Аналогично построим и сравним графики теоретической и эмпирической дифференциальных кривых распределения.
   
8. 
   Приводим графики к стандартному виду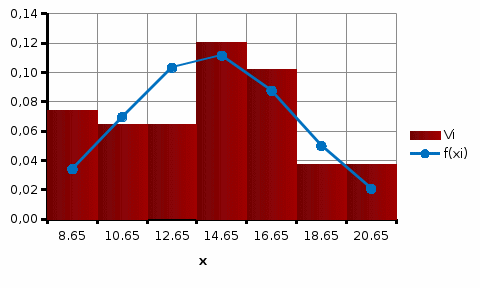
   

9. 
   Нашей задачей является сравнение эмпирических и теоретических 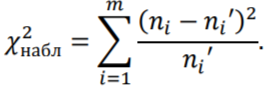частот по формуле.
   

10. 
    Составим вспомогательную таблицу из трех столбцов
    

ni	ni`=N*Pi	(ni-ni`)^2/ni`
8	3,675	5,089
7	7,504	0,034
7	11,142	1,540
13	12,030	0,078
11	9,445	0,256
4	5,393	0,360
4	2,239	1,385
54		8,742

Сумма и есть значение =8,742

Расхождение между статистическим и теоретическим распределениями является несущественным, если величина не превышает критического значения :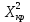



Вывод: Так как 8,742 то выдвинутую гипотезу о том, что случайная величина распределена по нормальному закону, можно с надежностью 1 – α = 0,95 считать правдоподобной, не противоречащей опытным данным.
2.3 Выполнение В

1. 
   Составляем таблицу
   

xi	ui	ф(ui)	f(xi)	Pi=hf(xi)	F(xj)
-0,65	-2,81	0,01	0,00	0,01	0,00
0,95	-2,00	0,05	0,03	0,04	0,02
2,55	-1,19	0,20	0,10	0,16	0,12
4,15	-0,39	0,37	0,19	0,30	0,35
5,75	0,42	0,37	0,18	0,29	0,66
7,35	1,22	0,19	0,09	0,15	0,89
8,95	2,03	0,05	0,03	0,04	0,98

2. 
   Вносим значения ф(ui)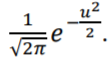
   

3. 
   С помощью полученных значений по формуле
   

где S – значение среднеквадратического отклонения.

4. 
   Вероятность попадания нормально распределенной случайной величины в i-тый интервал найдем по формуле:
   

Здесь h – интервал группирования. Для проверки правильности расчетов, вычислим сумму Pi.

5. 
   Для нахождения значений F(xj)воспользуемся встроенной функцией НОРМ.СТ.РАСП(z;интегральная)
   
6. 
   Для построения кривых теоретической и эмпирической интегральных функций распределения на одном графике выполним следующие шаги:
   

 скопируем из лабораторной работы №1 столбцы, содержащие правый край интервала группирования и значения эмпирической (наблюдаемой) функции.

 Добавим к скопированным столбец значений теоретической функции.

 Приведём график к стандартному виду, добавив координатные оси, подписи данных и т.д.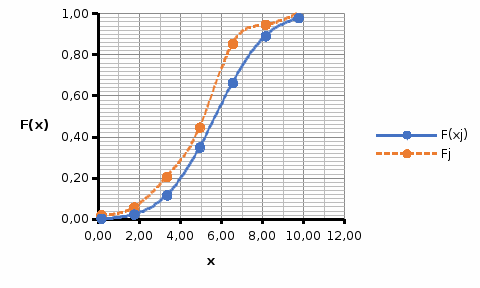

7. 
   Аналогично построим и сравним графики теоретической и эмпирической дифференциальных кривых распределения.
   
8. 
   Приводим графики к стандартному виду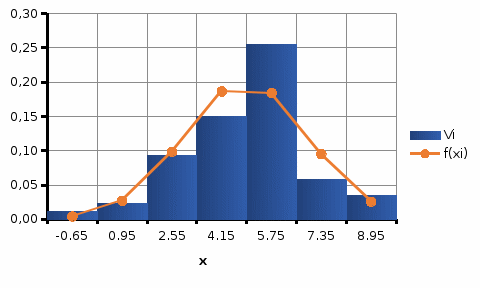
   

9. 
   Нашей задачей является сравнение эмпирических и теоретических 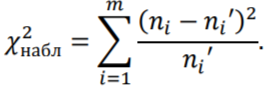частот по формуле.
   

10. 
    Составим вспомогательную таблицу из трех столбцов
    

ni	ni`=N*Pi	(ni-ni`)^2/ni`
1	0,337	1,303
2	2,345	0,051
8	8,510	0,031
13	16,113	0,601
22	15,920	2,322
5	8,208	1,254
3	2,208	0,284
54		5,845

Сумма и есть значение =5,845

Расхождение между статистическим и теоретическим распределениями является несущественным, если величина не превышает критического значения :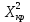



Вывод: Так как 5,845 то выдвинутую гипотезу о том, что случайная величина распределена по нормальному закону, можно с надежностью 1 – α = 0,95 считать правдоподобной, не противоречащей опытным данным.

3 Вывод к лабораторной работе

Смыслом выполнения данной лабораторной работы было вычисление функции Гаусса, гипотезы о нормальном законе распределения, критерий Неймана-Пирсона, стратегии Неймана-Пирсона. В итоге можно сказать, что, систематизировав данные, обработав их предложенными методами можно освоить тему «Построение теоретических интегральной и дифференциальной функций распределения» и использовать полученные знания в практических целях.

4 Список литературы

«Выполнение лабораторных работ по математической статистике в системе EXCEL», Авторы: Ю.И. Мещерякова, В.А. Сикорский. Москва 2019 г.