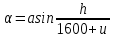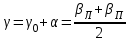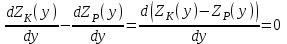Практические задания. детали машин №1. МОДЕЛИРОВАНИЕ ПОПЕРЕЧНОГО ПОЛОЖЕНИЯ КОЛЕС-НОЙ ПАРЫ В РЕЛЬСОВОЙ К. Моделирование поперечного положения колесной пары в рельсовой колее
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
УДК 51-74 В.О. Корчагин, М.А. Маслов Брянский государственный технический университет МОДЕЛИРОВАНИЕ ПОПЕРЕЧНОГО ПОЛОЖЕНИЯ КОЛЕСНОЙ ПАРЫ В РЕЛЬСОВОЙ КОЛЕЕ Выполнено моделирование поперечного положения колёсной пары в рельсовой колее. Рассмотрены вопросы аналитического анализа контактирования колеса и рельса для решения задач повышения энергоэффективности локомотива воздействием магнитного поля на зону контакта. Ключевые слова: моделирование, повышение энергоэффективности, площадь контакта, Сила трения между телами зависит от ряда факторов, среди них – величина фактической площади контакта [1, с. 217]. Известно [2, с. 50], что фактическая площадь контакта в 10-20 раз меньше контурной.Передаваемые усилия, микрогеометрия и макрогеометрия колеса и рельса оказывают влияние на величину пятна контакта, на трение и износ особеннона этапе приработки поверхностей [3-5]. Зная величину мгновенной площади контакта колеса с рельсом, представляется возможным формировать управляющий сигнал для системы регулирования устройства[6]. Плавное регулирование тока индуктора способствует поддержанию коэффициента сцепления колёс локомотива с рельсом в пределах требуемой величины, посредством воздействия на зону контакта магнитным полем. Радиус колеса, наличие возвышения рельса, уширение колеи, износ ходовых частей подвижного состава и верхнего строения пути участвуют в формировании пятна контакта. Изложенные факторы обуславливают перекос колёсной пары в колее на угол 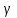 . Оценка влияния на размеры контактного пятна каждого фактора в отдельности позволит выделить наиболее значимые.Возвышение наружного рельса в криволинейном участке пути устраивается путём увеличения толщины балластного слоя под шпалой.При этом рельсовая колея наклоняется на угол . Оценка влияния на размеры контактного пятна каждого фактора в отдельности позволит выделить наиболее значимые.Возвышение наружного рельса в криволинейном участке пути устраивается путём увеличения толщины балластного слоя под шпалой.При этом рельсовая колея наклоняется на угол 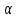 относительно края шпалы. относительно края шпалы.
где 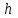 –величина возвышения наружного рельса, мм; –величина возвышения наружного рельса, мм;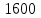 – расстояние между осями левого и правого рельса на прямом участке пути, мм; – расстояние между осями левого и правого рельса на прямом участке пути, мм;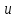 – уширение рельсовой колеи, мм. – уширение рельсовой колеи, мм.В рамках решения задачи по определению геометрических параметров положения колёсной пары железнодорожного подвижного состава в рельсовой колее написана «Программа моделирования поперечного положения колёсной пары в колее». Программа разработана в среде Visual LISP [7-9], для обмена данными с VisualBasicforApplications задействован интерфейс AutoCADActiveXAutomationInterface. Программный код включает 14 модулей на языке функционального программирования AutoLisp. Основные структурные данные языка представлены списками. Программа моделирования поперечного положения колёсной пары в колее позволяет исследовать контактирование профиля колеса с профилем рельса. В основе работы программы лежат итерационные алгоритмы. Для крайних и промежуточных положений рассчитывается смещение, наклон колёсной пары и угол контакта колеса с рельсом, определяется очертание и площадь поверхности контурного контакта. Промежуточные положения соответствуют случаю, когда гребни колёс не касаются рельса, одно из промежуточных положений является центральным. Крайние положения колёсной пары формируются как двухточечный контакт с левым и правым рельсом. К входным данным программы относятся параметры: минимальный зазор между колесом и рельсом для задания точности расчёта, число промежуточных положений колёсной пары, диаметр колеса по кругу катания, ве- 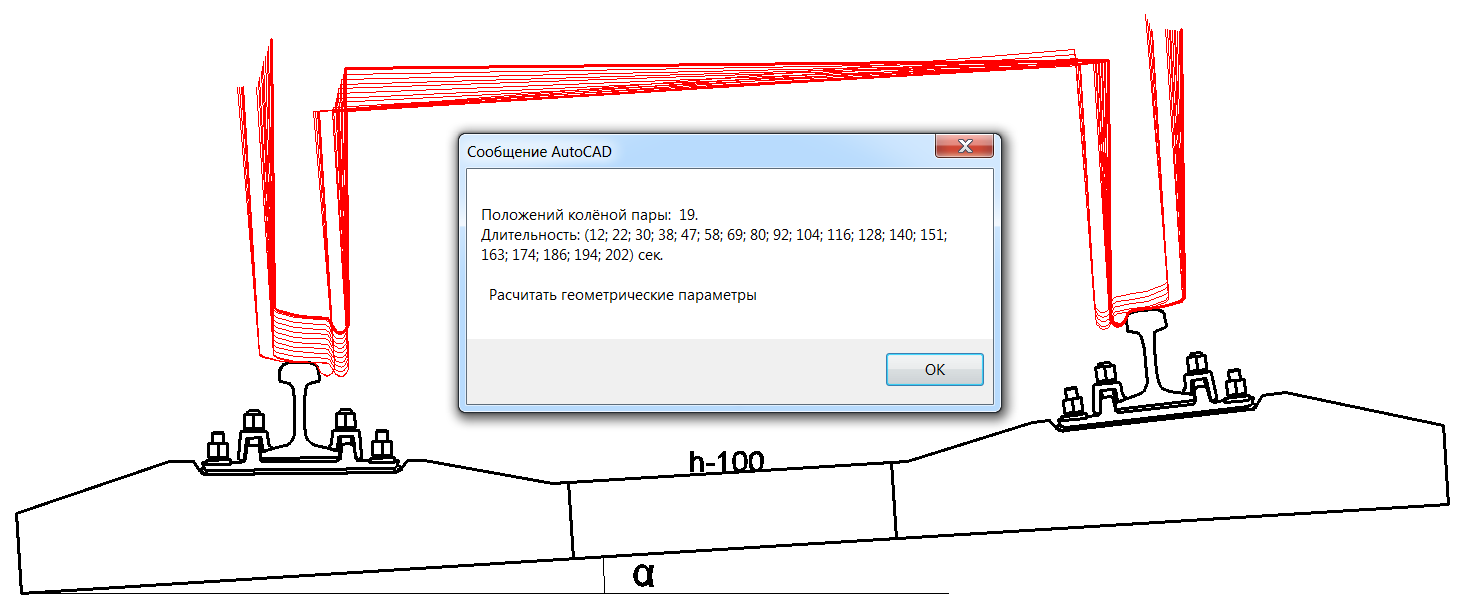 Рисунок 1. Итерационное определение положения колёсной пары в колее личина деформации на поверхности катания и гребне колеса, профиль колёсной пары, профиль левого и правого рельса, наличие возвышения рельса и уширения колеи. Искомые положения колёсной пары в рельсовой колее определяются итерациями плоскопараллельного перемещения профиля колёсной пары относительно профиля левого и правого рельса (рисунок 1). На каждом этапе контролируется зазор между поверхностями катания, гребнями колёс и рельсами. Выполнение условий величины минимальных зазоров позволяет перейти к расчёту следующего положения колёсной пары в колее. После построения поперечных положений колёсной пары в колее определяется величина контурной площади контакта колеса с рельсом (рисунок 2). 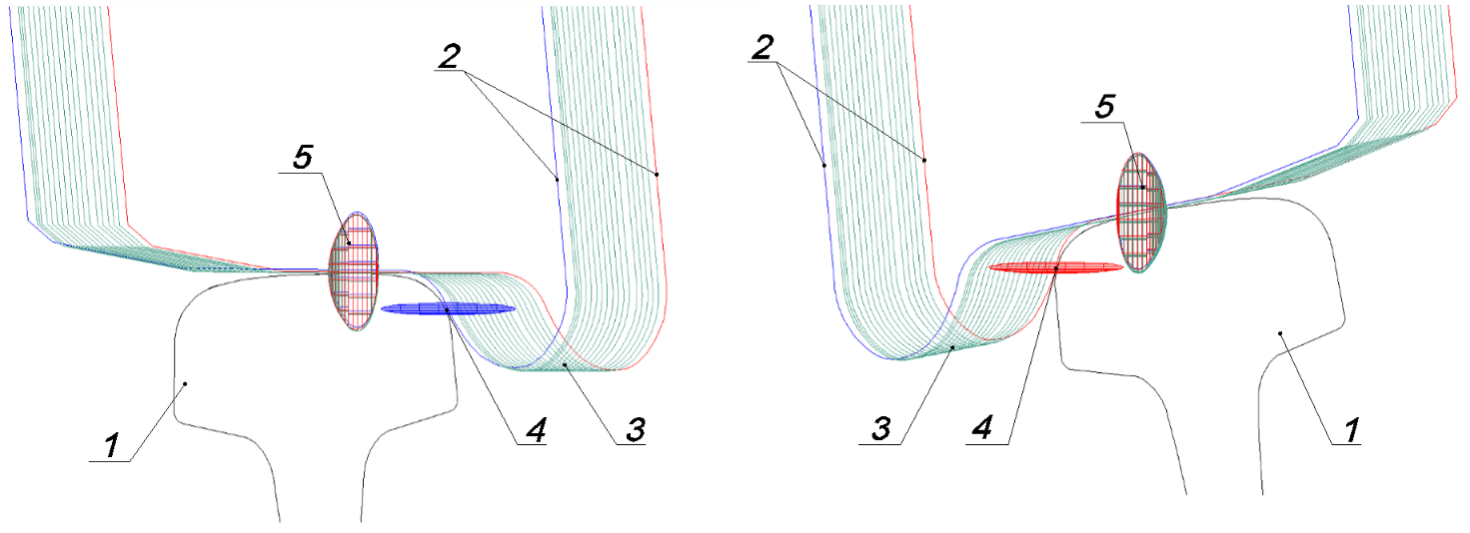 а) б) Рисунок 2. Контурная площадь контакта колеса с рельсом а – контакт с левым рельсом; б – контакт с правым рельсом; 1 – рельс; 2 – крайние положения колёс; 3 – промежуточные положения колёс; 4 – пятно контакта на гребне; 5 – пятно контакта на поверхности катания Точечный контакт, посредством смещения координат профиля на величину деформации, вырождается в область пересечения. Вращение нижней границы области пресечения относительно оси колёсной пары и вытягивание верхней границы области пресечения в продольном направлении формирует тело контакта, ограниченное поверхностями контурного контакта. Число выполненных итераций, время расчёта отображаются в информационных сообщениях. Результаты расчёта и геометрические параметры поперечных положений колёсной пары железнодорожного подвижного состава в рельсовой колее выводятся на экран и сохраняются в файл для дальнейшей обработки. Таблица 1 Геометрические параметры положений колёсной пары в колее (Dк=1050мм; h=100мм)
Таблица 2 Геометрические параметры положений колёсной пары в колее (Dк=1250мм; h=100мм)
Моделирование контактирования профилей новых локомотивных колёс диаметром 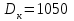 мм и мм и 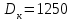 мм новыми рельсами Р65 выполнено для возвышения правого рельса мм новыми рельсами Р65 выполнено для возвышения правого рельса 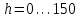 мм. Площадь контакта на поверхности катания левого и правого колеса возрастает по мере увеличения зазора мм. Площадь контакта на поверхности катания левого и правого колеса возрастает по мере увеличения зазора 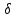 между гребнем колеса и рабочей гранью головки рельса. Разброс значений площади на поверхности катания для одного колеса не превышает13 мм².При контакте гребня с рельсом, когда между гребнем колеса и рабочей гранью головки рельса. Разброс значений площади на поверхности катания для одного колеса не превышает13 мм².При контакте гребня с рельсом, когда 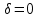 мм, прирост площади контакта колеса 1050 мм составляет 82…91 мм², колеса 1250 мм – 90…99 мм². Наибольший единовременный перекос площадей между левым и правым колесом при двухточечном контакте: мм, прирост площади контакта колеса 1050 мм составляет 82…91 мм², колеса 1250 мм – 90…99 мм². Наибольший единовременный перекос площадей между левым и правым колесом при двухточечном контакте: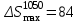 мм² и мм² и 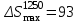 мм². График зависимости площади контакта мм². График зависимости площади контакта 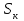 на поверхности катания колеса от зазора на поверхности катания колеса от зазора 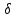 при различных возвышениях и диаметрах колёс представлен на рисунке 3. при различных возвышениях и диаметрах колёс представлен на рисунке 3.На зависимости 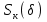 видны характерные участками возрастания ( видны характерные участками возрастания (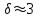 мм, мм,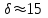 мм) и уменьшения ( мм) и уменьшения (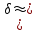 21мм и 21мм и 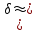 5мм) площади контакта. Данные всплески объясняются расположением контакта относительно перелома профиля колеса. Когда контакт приходится на перелом профиля, площадь уменьшается. Расположения контакта между переломами профиля соответствует возрастанию площади контакта. 5мм) площади контакта. Данные всплески объясняются расположением контакта относительно перелома профиля колеса. Когда контакт приходится на перелом профиля, площадь уменьшается. Расположения контакта между переломами профиля соответствует возрастанию площади контакта.Таким образом, для снижения разброса площади, требуется выполнить условие плавности изменения кривизны на поверхности катания. Иначе говоря, первая производная от функции профиля по горизонтальной координате должна быть гладкой функцией и не должна иметь разрывов.Профиль нового или недавно обточенного колеса не соответствует условию плавности изменения кривизны, такие ко- 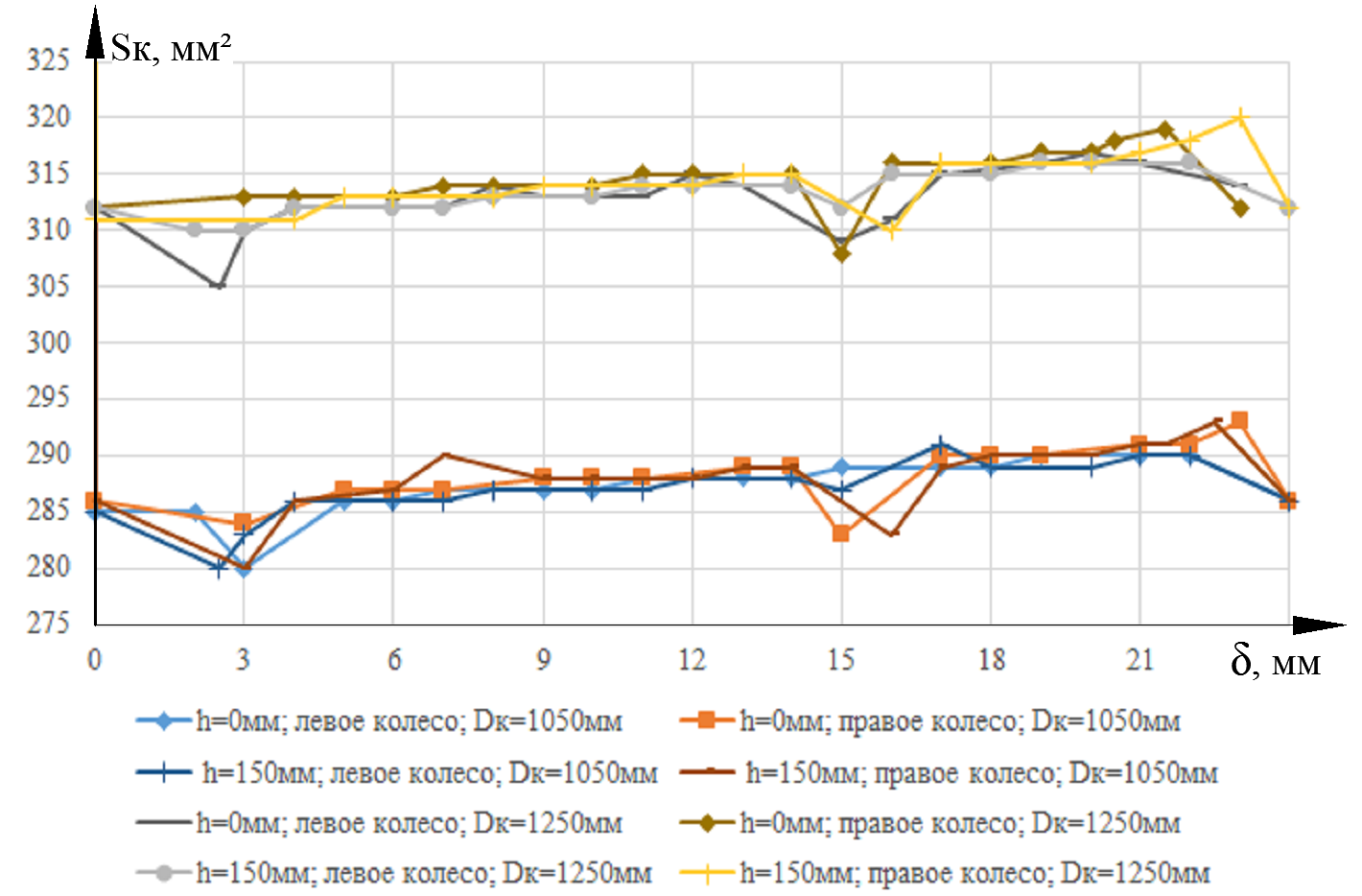 Рисунок 3. Зависимость площади контакта на поверхности катания колеса от зазора между гребнем и рельсом лёса склонны к буксованию. В процессе приработки поверхности катания колеса переломы профиля скругляются и функция профиля становится гладкой. Результаты моделирования позволяют выразить связь угла наклона колёсной пары, с углами контакта на поверхности катания колёс и возвышением.
где 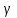 –угол наклона колёсной пары, °; –угол наклона колёсной пары, °;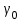 – угол наклона колёсной пары при нулевом возвышении, °; – угол наклона колёсной пары при нулевом возвышении, °;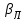 – угол контакта на поверхности катания левого колеса, °; – угол контакта на поверхности катания левого колеса, °;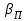 – угол контакта на поверхности катания правого колеса, °. – угол контакта на поверхности катания правого колеса, °.Профиль колеса аппроксимирован гладкой функцией 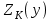 , представленной тригонометрическим рядом Фурье. При малом числе гармоник наблюдается явно выраженная пульсация со сменой монотонности аналитического графика. Направление профиля в каждой его точке характеризуется производной от функции профиля по горизонтальной координате. Поскольку от функции профиля берётся производная, поэтому следует сохранять монотонность исходной функции [10, с. 46]. Сходимость аналитического и исходного профиля колеса достигается при 20 гармониках. , представленной тригонометрическим рядом Фурье. При малом числе гармоник наблюдается явно выраженная пульсация со сменой монотонности аналитического графика. Направление профиля в каждой его точке характеризуется производной от функции профиля по горизонтальной координате. Поскольку от функции профиля берётся производная, поэтому следует сохранять монотонность исходной функции [10, с. 46]. Сходимость аналитического и исходного профиля колеса достигается при 20 гармониках.В условиях, когда боковая грань рельса обладает большой крутизной, сохранить монотонность, аппроксимируя рядом Фурье, не представляется возможным.Для аппроксимации рабочих поверхностей профиля рельса, согласно данным работы [11], воспользуемся полином 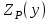 .В точке контакта колеса с рельсом направления профилей совпадают, а расстояние между профилями минимальное. .В точке контакта колеса с рельсом направления профилей совпадают, а расстояние между профилями минимальное.
Представляется возможным выполнить аналитический анализ контактирования колеса с рельсом путём сопоставления уравнений профилей и их производных. 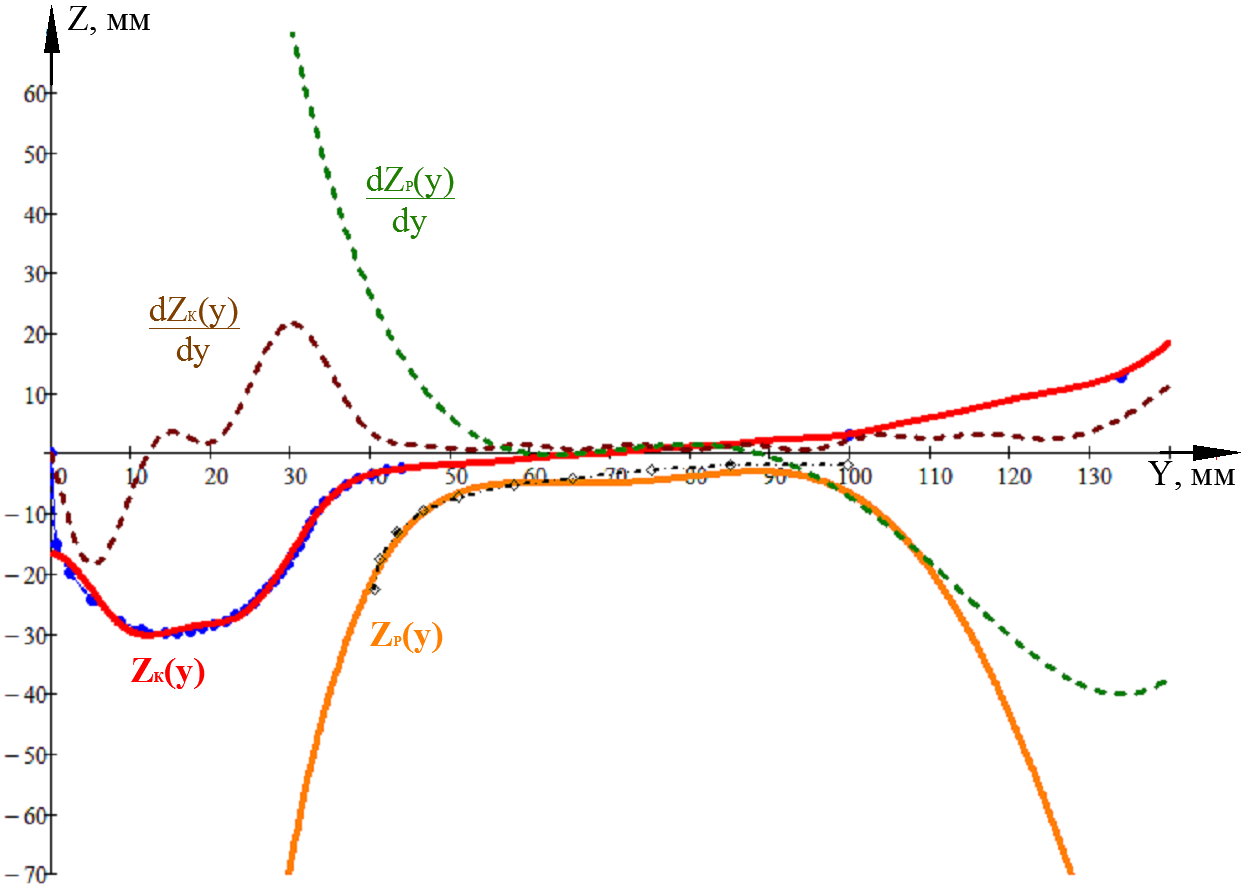 Рисунок 4. Функции профилей колеса и рельса и их производные Определение мгновенного зазора 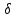 в условиях эксплуатации возможно посредством способа [12], основанного на видеосъёмке зоны контакта с последующей покадровой обработкой. Дальнейшие развитие вопроса заключается в исследовании влияния взаимного положения колеса и рельса на изменение параметров магнитного поля в зоне контакта. Величина магнитного сопротивления в зоне контакта зависит от положения колеса относительно рельса. Основываясь на данном утверждении, будем рассматривать способ [12] в качестве прототипа. Зависимостьмагнитного сопротивления от величины зазора в условиях эксплуатации возможно посредством способа [12], основанного на видеосъёмке зоны контакта с последующей покадровой обработкой. Дальнейшие развитие вопроса заключается в исследовании влияния взаимного положения колеса и рельса на изменение параметров магнитного поля в зоне контакта. Величина магнитного сопротивления в зоне контакта зависит от положения колеса относительно рельса. Основываясь на данном утверждении, будем рассматривать способ [12] в качестве прототипа. Зависимостьмагнитного сопротивления от величины зазора 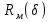 способствует мониторингу поперечного положения колёсной пары в колее и формированию данных для системыоперативного регулирования сцепления колеса с рельсом. способствует мониторингу поперечного положения колёсной пары в колее и формированию данных для системыоперативного регулирования сцепления колеса с рельсом.Список литературы 1. Крагельский, И.В. Развитие науки о трении [Текст] / И.В. Крагельский, В.С Щедров. – М.: изд-во АН СССР, 1956. – 237 с. 2. Керопян, А.М. Развитие теории взаимодействия и обоснование рациональных параметров системы колесо – рельс карьерных локомотивов в режиме тяги :дис. доктора техн. наук. – Екатеринбург, 2015. – 233 с. 3. Демкин, Н.Б. Качество поверхности и контакт деталей машин [Текст] / Н.Б. Демкин, Э.В. Коротков. – М.: Машиностроение, 1981. – 244 с. 4. Михин, Н.М. Внешнее трение твёрдых тел [Текст] / Н.М. Михин. – М.: Наука, 1977. – С. 53 – 56. 5. Комбалов, В.С. Влияние шероховатости твёрдых тел на трение и износ / В.С. Комбалов– М.: Наука, 1974. – 112 с. 6. Патент РФ № 2015109505/11, 18.03.2015. Устройство для предотвращения буксования локомотива. // Патент России № 156444. 2015. Бюл. № 31. / Воробьев В.И., Антипин Д.Я., Пугачев А.А., Измеров О.В., Бондаренко Д.А., Корчагин В.О. 7. Полещук, Н.Н. AutoLisp и VisualLISP в среде AutoCAD [Текст] / Н.Н. Полещук, П.В. Лоскутов. – СПб.: БХВ-Петербург, 2006. – 960 с.: ил. – ISBN 5-94157-738-9. 8. Полещук, Н.Н. AutoCAD 2012 [Текст] / Н.Н. Полещук. – СПб.: БХВ-Петербург, 2012. – 752 с.: ил.+CD-ROM –ISBN 987-5-9775-0709-7. 9. Джамп, Д. AutoCAD. Программирование [Текст] / Д. Джамп. Пер. с англ.– М.: Радио и связь, 1992. – 336 с.: ил. – ISBN 5-256-00807-2. 10. Калиткин, Н.Н. Численные методы [Текст] / Н.Н. Калиткин. – М.: Наука, 1978. – 512 с. 11. Сакало, А.В. Математическое моделирование профилей изношенных поверхностей тел качения [Текст] / А.В. Сакало // Вестник БГТУ. – Брянск БГТУ, 2009. – № 3. – С. 78-82. 12. Патент РФ № 2010108960/11, 10.03.2010. Способ определения бокового усилия прижатого колеса на рельс при движении железнодорожного состава. // Патент России № 2426664. 2010. Бюл. № 23. / Ватонин А.А., Аккерман С.Г., Аккерман Г.Л. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||