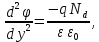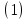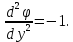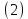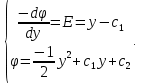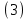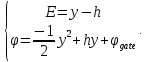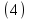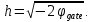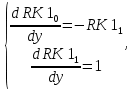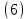эссе. Моделирование процесса проникновения электрического поля в полупроводник в среде
 Скачать 98.95 Kb. Скачать 98.95 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ФЭТ отчет по лабораторной работе № 1 по дисциплине «КТиМвЭл» Тема: Моделирование процесса проникновения электрического поля в полупроводник в среде MathCAD
Санкт-Петербург 2021 Цель работы. Исследовать распределения электрического поля и потенциала в глубине полупроводника при приложении к затвору постоянного потенциала в случае резкой границы обедненной области. Исследование выполнено с помощью аналитического метода и метода Рунге – Кутты. Основные теоретические положения. Полевым транзистором называется полупроводниковый прибор с тремя выводами: истоком, затвором и стоком. Ток, протекающий по проводящему каналу между истоком и стоком, управляется напряжением на затворе. В данной работе исследуются процессы проникновения электрического поля, создаваемого затвором, в глубину полупроводника, т. е. процессы образования обеднённой области, рис. 1. 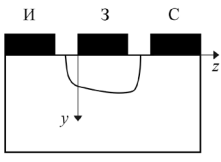 Рисунок 1. Структура полевого транзистора Шоттки В наиболее простом случае предполагается фантазийное отсутствие теплового размытия границы обеднённой области. Тогда уравнение Пуассона для электрического потенциала в обеднённой области примет вид:
где 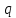 – заряд электрона, равный – заряд электрона, равный 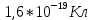 , , 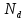 – концентрация доноров, – концентрация доноров, 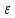 – относительная диэлектрическая проницаемость, – относительная диэлектрическая проницаемость, 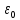 – диэлектрическая постоянная. – диэлектрическая постоянная.Для решения уравнения методом Рунге-Кутта необходимо ввести нормировку, а именно: потенциал (и всё, что измеряется в вольтах) соотнести с тепловым потенциалом, равным 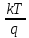 ; длины (и всё, что измеряется в метрах) соотнести с длиной Дебая ; длины (и всё, что измеряется в метрах) соотнести с длиной Дебая 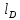 , равной , равной 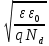 . .Тогда уравнение (1) примет вид (теперь и далее все величины нормированы):
Уравнение (2) может быть решено как аналитически, так и компьютерным моделированием методом Рунге-Кутта. 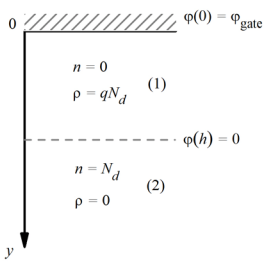 Рисунок 2. Геометрия задачи Задача Коши для решения уравнения (1) состоит из условий для электрического потенциала электрического поля при 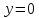 , т. е. в подзавтворной области, и электрического поля на глубине , т. е. в подзавтворной области, и электрического поля на глубине 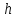 , начиная с которой электрический потенциал отсутствует. , начиная с которой электрический потенциал отсутствует.Аналитическое решение уравнение (2) достигается путём двойного интегрирования. Имеем:
Решение задачи Коши: 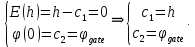 В итоге система уравнений (3) имеет вид:
Из уравнения для электрического потенциала в системе уравнений (3) глубина проникновения 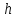 может быть выражена через потенциал на затворе при условии может быть выражена через потенциал на затворе при условии 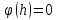 . Тогда имеем: . Тогда имеем:
Моделирование. Вариант 8. Дано: 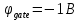 , , 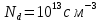 , , 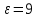 , , 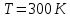 . .Тепловой потенциал: 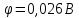 . Длина Дебая: . Длина Дебая: 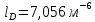 . .Нормирование 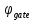 приводит к значению: приводит к значению: 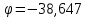 . .Нормированная глубина проникновения, рассчитанная по формуле (5): 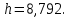 Аналитическое решение. На рисунке 3 представлены графики для уравнений (4) электрического потенциала и электрического поля в нормированных величинах. 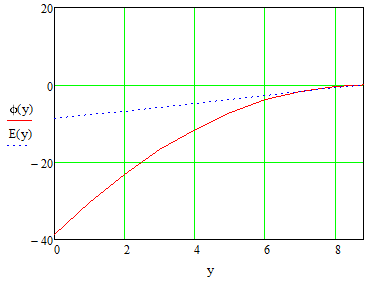 Рисунок 3. Графики 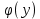 и и  в нормированных величинах. в нормированных величинах.Решение методом Рунге-Кутта. Так как метод Рунге-Кутта может быть применим только к дифференциальным уравнениям первого порядка, то уравнение Пуассона (2) необходимо свести к системе уравнений:
где 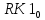 и и 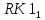 – обозначения для – обозначения для 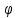 и и 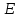 соответственно. соответственно.Функция MathCAD для применения метода Рунге-Кутта есть: 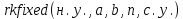 , где н.у. – вектор начальных условий, , где н.у. – вектор начальных условий, 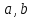 - нижний и верхний пределы изменения переменной соответственно, - нижний и верхний пределы изменения переменной соответственно, 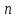 – число точек на отрезке – число точек на отрезке 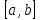 , с.у. – система уравнений для решения. , с.у. – система уравнений для решения.Имеем: 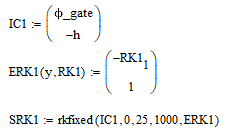 В таблице 1 приведена часть значений решения методом Рунге-Кутта. Столбец под номер «0» есть столбец нормированных значений координаты 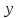 , под номером «1» - значения электрического потенциала, «2» - электрического поля. , под номером «1» - значения электрического потенциала, «2» - электрического поля.Таблица 1. Решение методом Рунге-Кутта. 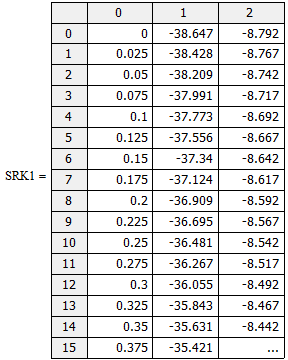 На рисунке 4 представлены графики решения системы (6), полученные методом Рунге-Кутта. 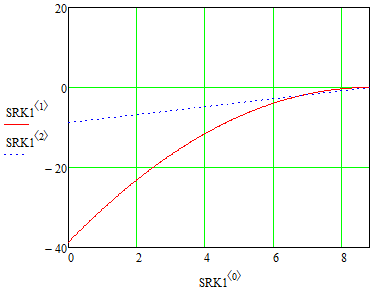 Рисунок 4. Графики решения системы (6) Визуальное сравнение рисунков 3 и 4 показывает хорошее совпадение решений аналитическим методом и методом Рунге-Кутта. На рисунке 5 представлены графики с размерными величинами. 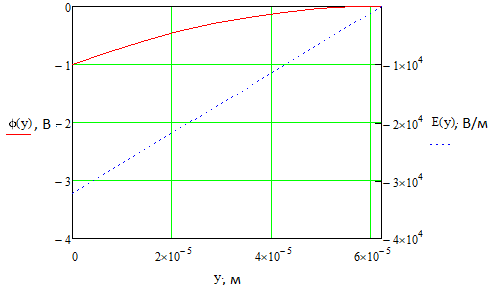 Рисунок 3. Графики 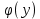 и и  в размерных величинах. в размерных величинах.Выводы. В данной работе было проведено моделирование в среде MathCAD 14.0 процесса проникновения электрического поля в полупроводник при условии отсутствия теплового размытия границы. В этом случае уравнения Пуассона для электрического потенциала допускают аналитическое решение, с которым совпало решение полученное методом Рунге-Кутта, что видно при сравнении рисунков 3 и 4. |