ФизЛаз№1. Моделирование усилителя бегущей волны в стационарном режиме
 Скачать 189.69 Kb. Скачать 189.69 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра фотоники отчет по лабораторной работе №1 по дисциплине «Физика лазеров» Тема: «Моделирование усилителя бегущей волны в стационарном режиме»
Санкт-Петербург 2021 Цель работы. Моделирование усилителя бегущей волны в стационарном режиме. Основные теоретические положения. Квантовые усилители служат для того, чтобы увеличить напряженность поля электромагнитной волны, поступающей на их вход. В квантовом усилителе электромагнитные колебания усиливаются при взаимодействии с квантовой системой частиц (атомов, молекул, ионов) за счёт вынужденного излучения [1]. Если число актов вынужденного излучения, вызванного падающей волной, превышает число актов вынужденного поглощения, то среда усиливает эту волну. Для этого в среде должно быть достигнуто состояние инверсной заселенности. Инверсная заселенность энергетических уровней - неравновесное состояние среды, при котором число частиц (атомов, молекул), находящихся на верхних энергетических уровнях, т. е. в возбужденном состоянии, больше, чем число частиц, находящихся на нижних энергетических уровнях. Основная проблема создания квантовых усилителей – получение состояния рабочего вещества с инверсией населенностей. В настоящее время предложено и осуществлено очень много способов создания инверсии населенностей в различных веществах, находящихся в твёрдом, жидком и газообразном состоянии, и на их основе осуществлены разнообразные квантовые усилители, работающие в широком диапазоне волн. Квантовые усилители можно разделить на два класса, различающихся главным образом диапазоном частот, а, следовательно, и типами активных сред и также областями применения, - это квантовые усилители СВЧ-диапазона и усилители оптического диапазона. В данной работе исследуется квантовый усилитель оптического диапазона. Оптический квантовый усилитель (ОКУ) представляет собой устройство, позволяющее усиливать когерентное излучение оптического диапазона. Возможны два режима работы ОКУ: бегущей волны (без обратной связи) и регенеративный (с положительной обратной связью, создаваемой с помощью открытых резонаторов). В данной работе исследуется ОКУ бегущей волны Пусть плоская волна падает на лазерный усилитель длиной l вдоль оси z. Уравнение переноса излучения в активной среде записывается в виде 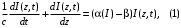 где I(z,t) – интенсивность излучения; t – время, z – координата, вдоль которой распространяется излучение; – коэффициент нерезонансных потерь; (I) – зависящий от интенсивности коэффициент усиления. В стационарном случае интенсивность не меняется со временем и первый член в уравнении переноса будет равен нулю. Тогда уравнение переноса принимает вид 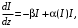 где 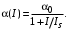 Здесь 0 – линейный коэффициент усиления (коэффициент усиления слабого сигнала), Is – интенсивность насыщения) . Здесь 0 – линейный коэффициент усиления (коэффициент усиления слабого сигнала), Is – интенсивность насыщения) .Под интенсивностью насыщения понимают интенсивность, при которой коэффициент усиления падает в два раза по сравнению с линейным. Действительно, при I = Isкоэффициент (I) =0/2. Таким образом, уравнение переноса можно записать как 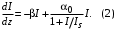 Проанализируем это выражение. Рассмотрим три случая для различных диапазонов интенсивностей: 1. I < В этом случае I/ Is<<1. Тогда 1+ I/ Is1 и 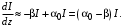 Решив это уравнение с начальным условием I (z= 0) = I0, I0 – интенсивность, падающая на вход усилителя, получим 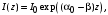 Таким образом, при малых уровнях сигнала наблюдается экспоненциальный рост интенсивности вдоль координаты (линейное усиление). 2. I >> Is. В этом случае I/Is>> 1. Тогда 1+ I/Is I/Isи 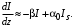 При значительных входных сигналах рост выходной энергии замедляется и, начиная с некоторой интенсивности, вообще прекращается. Стационарное значение интенсивности излучения достигается, когда все, что может излучить единичный отрезок длины активного вещества в режиме полного насыщения, поглощается за счет нерезонансных потерь в том же отрезке. Этот баланс поглощенной и излученной энергий приводит к исчезновению дальнейшего усиления по мере распространения вдоль усилителя. Если интенсивность достигает предельного значения Iпред, то это значит, что дальнейшего усиления нет и dI/dz = 0. Тогда можем записать: 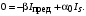 Отсюда получаем, что 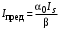 . Таким образом, в усилителе бегущей волны предельная выходная интенсивность определяется, а конечном счете интенсивностью насыщения, коэффициентом линейного усиления и коэффициентом нерезонансных потерь. . Таким образом, в усилителе бегущей волны предельная выходная интенсивность определяется, а конечном счете интенсивностью насыщения, коэффициентом линейного усиления и коэффициентом нерезонансных потерь.3. IIS. Проинтегрировав уравнение переноса 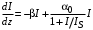 по длине l, получим: по длине l, получим: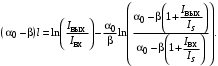 (3) (3)Это уравнение в общем виде не имеет аналитического решения и решается только численно. Обработка результатов. Численное решение уравнения в Mathcad (1 случай). Решим численно уравнение в среде Mathcad для диапазона 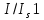 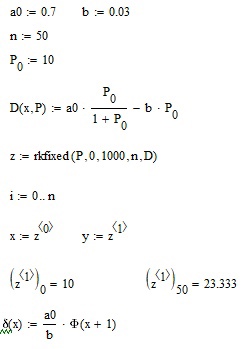 Найдём аналитическое решение с помощью аппроксимации: 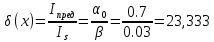 Построим график численного решения с указанием предельного значения. 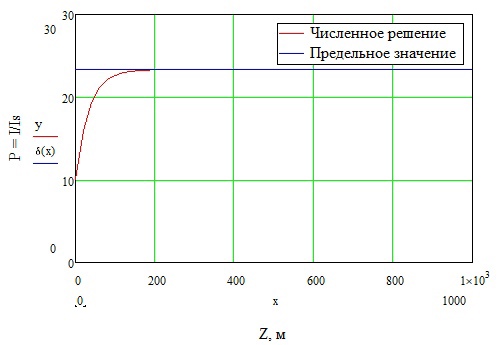 Рис.1 – График решения уравнения при I/Is>> 1 Запишем результаты в таблицу: Таблица 1 – Численное решение уравнения
Численное решение уравнения в Mathcad (2 случай). Решим численно уравнение в среде Mathcad для диапазона I/Is<<1: 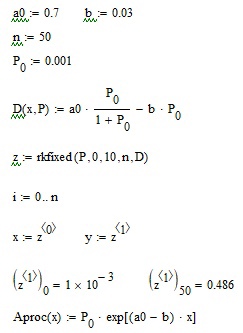 Построим графики численного метода и аналитического приближения. 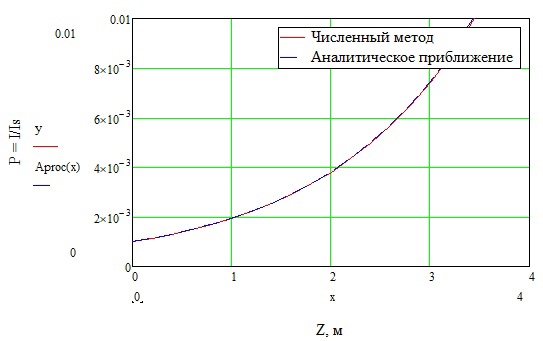 Рис. 2 – График решения уравнения при I/Is <<1 Запишем результаты в таблицу: Таблица 2 – Численное решение уравнения
Выводы. В ходе лабораторной работы был рассмотрен численный метод расчёта усилителя бегущей волны в стационарном режиме в программе Mathcad, а также аналитические приближения в предельных случаях. Результаты в предельных случаях были сравнены с аналитическими аппроксимациями на пределах диапазона. Из графиков (рис.1 и рис.2) видно, что результаты, полученные численным методом, сходятся с результатами, полученными с помощью аппроксимации. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
