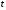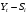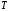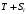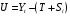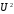Модуль Модели временных рядов

• Название: Модуль Модели временных рядов
• Дата: 16.04.2022
• Размер: 72.75 Kb.
• Имя файла: 36058.docx
• Тип: Документы; #477549

Модуль 2. Модели временных рядов.

Задание 3.

1. Постройте аддитивную модель временного ряда, последовательно выделив сезонную, трендовую и случайную компоненты.

2. Используйте полученную модель для краткосрочного прогнозирования.

3. Проверьте качество модели.

4. Индекс объема выпуска промышленной продукции в РФ с 20*2 по 20*3 гг. характеризуется следующими данными:

Год Месяц	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
20*2	125,01	126,41	137,67	125,95	119,12	123,49	112,3	108,83	112,09	117,61	121,89	125,6
20*3	146,0	141,52	156,23	143,82	139,01	143,49	142,91	148,31	147,92	154,72	145,97	151,35

К заданию 2) – прогноз на 2 квартал 20*4 г.

Решение

Построим график временного ряда: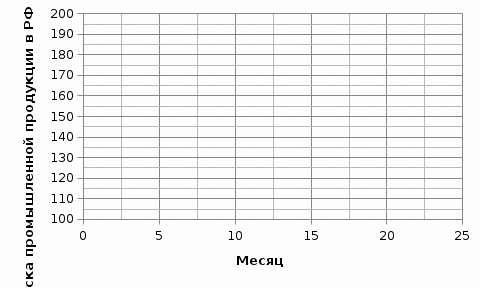


Проведем выравнивание ряда методом скользящей средней. Для этого просуммируем уровни ряда по 4 кварталам последовательно. Далее разделим полученные суммы на 4 и найдем скользящие средние, уже не содержащие сезонной компоненты. Найдем центрированные скользящие средние, для чего вычислим средние значения из двух последовательных скользящих средних. Вычислим оценки сезонной компоненты как разность между фактическим уровнем продаж и центрированными скользящими средними.

.

		Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	125,01	-	-	-
2	126,41	128,76	-	-
3	137,67	127,288	128,024	9,646
4	125,95	126,558	126,923	-0,972
5	119,12	120,215	123,386	-4,266
6	123,49	115,935	118,075	5,415
7	112,3	114,178	115,056	-2,756
8	108,83	112,708	113,443	-4,613
9	112,09	115,105	113,906	-1,816
10	117,61	119,298	117,201	0,409
11	121,89	127,775	123,536	-1,646
12	125,6	133,753	130,764	-5,164
13	146	142,338	138,045	7,955
14	141,52	146,893	144,615	-3,095
15	156,23	145,145	146,019	10,211
16	143,82	145,638	145,391	-1,571
17	139,01	142,308	143,973	-4,963
18	143,49	143,43	142,869	0,621
19	142,91	145,658	144,544	-1,634
20	148,31	148,465	147,061	1,249
21	147,92	149,23	148,848	-0,928
22	154,72	149,99	149,61	5,11
23	145,97	-	-	-
24	151,35	-	-	-

Используем полученные оценки сезонной компоненты для расчета сезонности S. Для этого найдем средние квартальные оценки сезонной компоненты, использовав данные всех кварталов. Заметим, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю, поэтому значения сезонной компоненты корректируются на величину, полученную как частное от деления суммы оценок сезонных компонент на число сезонов.

Показатели	1	2	3	4
1	-	-	9,646	-0,972
2	-4,266	5,415	-2,756	-4,613
3	-1,816	0,409	-1,646	-5,164
4	7,955	-3,095	10,211	-1,571
5	-4,963	0,621	-1,634	1,249
6	-0,928	5,11	-	-
Всего за период	-4,018	8,46	13,821	-11,071
Средняя оценка сезонной компоненты	-0,804	1,692	2,764	-2,214
Скорректированная сезонная компонента, Si	-1,163	1,332	2,405	-2,574

Для данной модели имеем: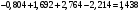



Корректирующий коэффициент: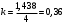

Рассчитываем скорректированные значения сезонной компоненты 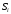и заносим полученные данные в таблицу.

Устраним сезонную компоненту из исходных уровней ряда и получим выравненные данные:

1	125,01	-1,163	126,173	116,388	115,225	9,785	95,742
2	126,41	1,332	125,078	117,924	119,257	7,153	51,171
3	137,67	2,405	135,265	119,46	121,865	15,805	249,808
4	125,95	-2,574	128,524	120,996	118,422	7,528	56,67
5	119,12	-1,163	120,283	122,532	121,369	-2,249	5,057
6	123,49	1,332	122,158	124,068	125,4	-1,91	3,648
7	112,3	2,405	109,895	125,604	128,008	-15,708	246,747
8	108,83	-2,574	111,404	127,139	124,566	-15,736	247,607
9	112,09	-1,163	113,253	128,675	127,512	-15,422	237,843
10	117,61	1,332	116,278	130,211	131,544	-13,934	194,143
11	121,89	2,405	119,485	131,747	134,152	-12,262	150,348
12	125,6	-2,574	128,174	133,283	130,709	-5,109	26,102
13	146	-1,163	147,163	134,819	133,656	12,344	152,383
14	141,52	1,332	140,188	136,355	137,687	3,833	14,692
15	156,23	2,405	153,825	137,891	140,295	15,935	253,92
16	143,82	-2,574	146,394	139,426	136,853	6,967	48,546
17	139,01	-1,163	140,173	140,962	139,799	-0,789	0,623
18	143,49	1,332	142,158	142,498	143,83	-0,34	0,116
19	142,91	2,405	140,505	144,034	146,439	-3,529	12,451
20	148,31	-2,574	150,884	145,57	142,996	5,314	28,239
21	147,92	-1,163	149,083	147,106	145,943	1,977	3,91
22	154,72	1,332	153,388	148,642	149,974	4,746	22,525
23	145,97	2,405	143,565	150,177	152,582	-6,612	43,72
24	151,35	-2,574	153,924	151,713	149,139	2,211	4,886
Итого:						0	2150,898

Определим компоненту Т. Для этого проведем аналитическое выравнивание ряда 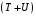с помощью линейного тренда.

Воспользуемся инструментом добавления тренда MS Excel


Имеем линейный тренд вида:

T = 114,852+1,5359t; R²=0,5578

Следовательно, можно сказать, что аддитивная модель объясняет 56% общей вариации уровней временного ряда.

Подставляя в уравнение тренда последовательно t= 1,…,20, получим значения тренда для каждого уровня временного ряда (столбец 5, табл. 5.8).

Найдем значения уровней ряда, полученные по аддитивной модели как (T+S) и рассчитаем абсолютную ошибку как U=y_i-(T+S).

Прогнозирование по аддитивной модели.

Прогнозное значение F_t уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда: T = 114,852 + 1,536t

Прогноз на 1 период: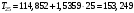

Значение сезонной компоненты за соответствующий период равно: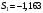
Таким образом,

Прогноз на 2 период: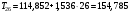

Значение сезонной компоненты за соответствующий период равно: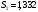

Таким образом,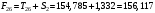

Прогноз на 3 период: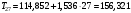

Значение сезонной компоненты за соответствующий период равно: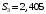
Таким образом,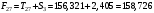

Прогноз на 4 период: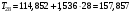

Значение сезонной компоненты за соответствующий период равно: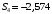

Таким образом,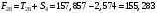

Список использованной литературы

1. 
   Доугерти К. Введение в эконометрику: Пер. с англ. — М: ИНФРА-М, 2009. — XIV, 402 с.
   
2. 
   Елисеева И.И. Эконометрика: учебник для магистров / И.И. Елисеева [и др]; под ред. И.И. Елисеевой. – М.: Издательство Юрайт, 2014. – 453 с.
   
3. 
   Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред.проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.
   
4. 
   Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 2007. – 304 с.
   
5. 
   Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный уцрс: Учеб. – 6-е изд., перераб. и доп. – М.: дело, 2004. – 576 с.
   
6. 
   Мхитарян В.С.. Эконометрика: учеб. / под ред. д-ра наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – 384 с.
   
7. 
   Новиков А.И. Эконометрика: Учебное пособие. – М.: Российский университет кооперации, 2008. – 137 с.
   
8. 
   Орлов А.И. Эконометрика: Учебник для вузов / А.И. Орлов. – 3-е изд., перераб. и доп. – М.: Издательство «Экзамен», 2004. – 576 с.