Задачи по статистике. Задача 1 Определяем цепные и базисные показатели ряда динамики
 Скачать 366.05 Kb.
|
|
Задача № 1 Определяем цепные и базисные показатели ряда динамики  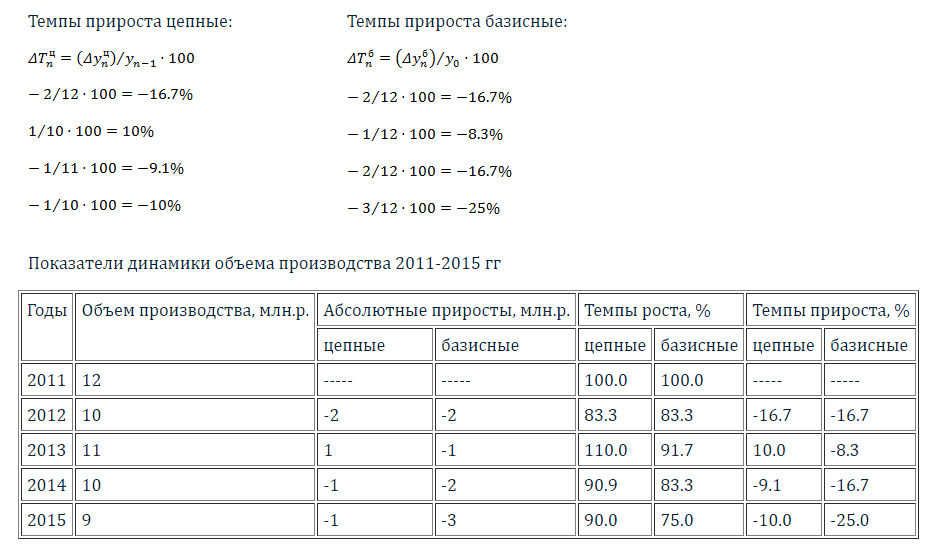  Задача № 2 Средние квартальные и среднегодовые остатки вкладов по отделению банка определим по формуле:  Среднеквартальные остатки вкладов: Iквартал:  IIквартал  IIIквартал  VIквартал  Среднегодовой остаток вкладов:  Проведем сглаживание ряда динамики методом трехчленной скользящей средней: В основу этого метода положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии. Для выявления основной тенденции развития методом скользящей средней прежде всего устанавливаются ее звенья. Звенья скользящей средней должны составляться из числа уровней, отвечающих длительности внутригодовых циклов в изучаемом явлении. Найдем скользящие средние:   и т.д. Для определения сглаженных уровней проводится центрирование (  ):  и т.д. Таблица 5 - Расчет скользящих средних.
Проведем сглаживание ряда динамики методом аналитического выравнивания прямой: Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития  рассчитывается как функция времени Определение теоретических (расчетных уравнений)  производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда динамики.Подбор адекватной функции осуществляется методом наименьших квадратов – минимальностью отклонений суммы квадратов между теоретическими и эмпирическими уровнями. Значения уравнения состоит в том, что при изучении тренда оно принимается в качестве критерия оценки соответствия расчетных (теоретических) уровней с фактическими (эмпирическими ) уровнями ряда динамики. Вычислим цепной темп роста (темп роста по годам) и цепной абсолютный прирост по формулам: 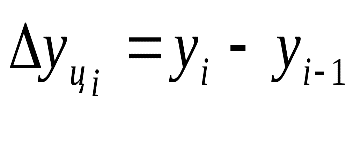 и Таблица 6. – Темп роста и абсолютный прирост.
Из таблицы видно, что остатки вкладов увеличиваются равномерно, поэтому для аналитического выравнивания применяется функция Т  аблица 7 – Промежуточные расчеты.
Находим a0 иa1по формулам:  ; .  По вычисленным параметрам производим синтезирование трендовой модели функции по формуле:               Правильность расчетов проверяется по равенству:  Несовпадение в равенстве на 0,001 тыс. руб. объясняется округлениями в расчетах. Параметр a0показывает, что остатки вкладов отделения банка в среднем возрастали на 174,731 тыс. руб. в месяц. 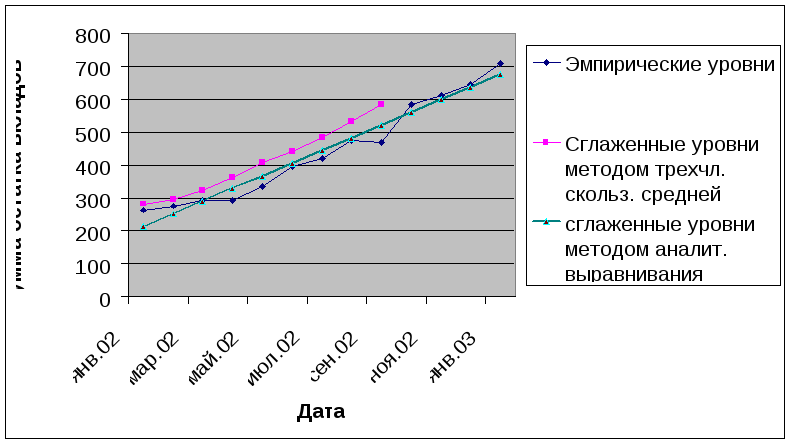 Рисунок 2. – Динамика остатков вкладов по отделению банка. Определим ожидаемые остатки вкладов на 01.04.2022г. по формуле:  Где l– срок прогноза.       Таблица 8. – Ожидаемые уровни остатков вкладов.
Изобразим на графике ожидаемые уровни остатков вкладов: 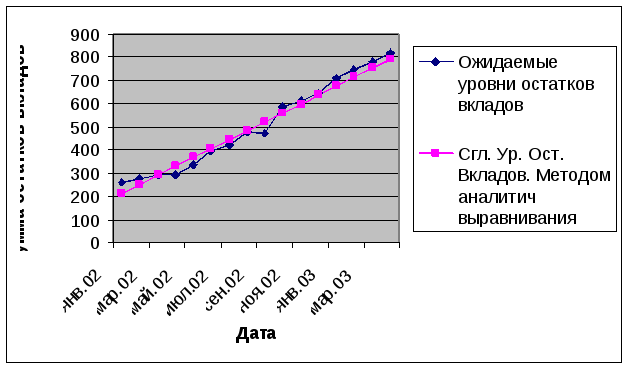 Рисунок 3 – Ожидаемые уровни остатков вкладов |
