Задачи множества. Можно сделать такую запись определения множества

• Название: Можно сделать такую запись определения множества
• Анкор: Задачи множества
• Дата: 25.04.2023
• Размер: 45.88 Kb.
• Имя файла: Задачи множества.docx
• Тип: Документы; #1088848

Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.

Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.

Можно сделать такую запись определения множества:

, где

“ ” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.

Два множества будем называть равными, если они состоят из одних и тех же элементов

Например: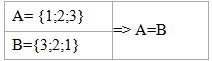



Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если  , то  , где “С” знак подмножества или включения.

Графически это выглядит так (рис.1):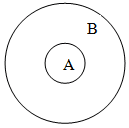



(рис.1)

Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.



Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).

Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.

Это определение можно записать с помощью обозначений:

А υ В, где   

где “ υ ” – знак объединения,

“ / ” – заменяет слова ”таких что“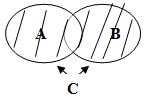



(рис.2)

Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:

А ∩ В = С, где 

“∩“ – знак пересечения. (рис.3)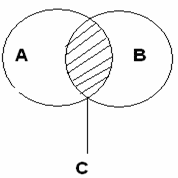



(рис.3)

Обозначим буквой Е основное или универсальное множество, где   A С Е (“ ”- любо число), т.е. А  Е = Е; А Е =А

Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕ или Ā (рис.4)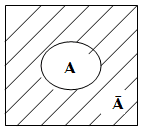

Е

(рис.4)

Примерами для понимания этих понятий являются свойства:

_

А  Ā=Е                      Ø = Е             Е Ā=Ā

_

А ∩ Ā= Ø                 Ē = Ø             (Ā)=А

Свойства дополнения имеют свойства двойственности:

________ _ _

А В = А∩В

________ _ _

А В = АUВ

Введем еще одно понятие – это мощность множества.

Для конечного множества А через m (A) обозначим число элементов в множестве А.

Из определение следуют свойства:

m (A) + m (Ā) = m (E)

А = В => m(A) = m(B)

Для любых конечных множеств справедливы так же утверждения:

m (A B) =m (A) + m (В) – m (А∩В)

m (A∩B) = m (A) + m (В) – m (А В)

m (A B C) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).

А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.

Задача №1

В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.

По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.

1. 
   Сколько учащихся решили все задачи?
   
2. 
   Сколько учащихся решили только две задачи?
   
3. 
   Сколько учащихся решили только одну задачу?
   

Задача № 2

Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.

Сколько студентов успешно решили только одну контрольную работу?

Задача № 3

В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.

Сколько учеников пользуются только одним видом транспорта?

Решение задачи № 1

Запишем коротко условие и покажем решение:

• 
  m (Е) = 40
  
• 
  m (А) = 20
  
• 
  m (В) = 18
  
• 
  m (С) = 18
  
• 
  m (А∩В) = 7
  
• 
  m (А∩С) = 8
  
• 
  m (В∩С) = 9
  

___________

m (А В С) = 3 => m (А В С) = 40 – 3 = 37

Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).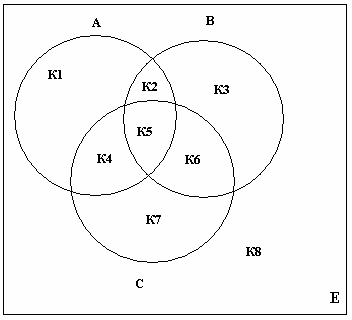



(рис.5)

К1 – множество учеников, решивших только одну задачу по алгебре;

К2 – множество учеников, решивших только две задачи по алгебре и геометрии;

К3 – множество учеников, решивших только задачу по геометрии;

К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;

К5 – множество всех учеников, решивших все три задачи;

К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;

К7 – множество всех учеников, решивших только задачу по тригонометрии;

К8 – множество всех учеников, не решивших ни одной задачи.

Используя свойство мощности множеств и рисунок можно выполнить вычисления:

• 
  m (К5) = m (А∩В∩С)= m (А В С) - m (А) - m (В) - m (С) + m (А∩В) + m (А∩С) + m (В∩С)
  
• 
  m (К5) = 37-20-18-18+7+8+9=5
  
• 
  m (К2) = m (А∩В) - m (К5) = 7-5=2
  
• 
  m (К4) = m (А∩С) - m (К5) = 8-5=3
  
• 
  m (К6) = m (В∩С) - m (К5) = 9-5=4
  
• 
  m (К1) = m (А) - m (К2) - m (К4) - m (К5) = 20-2-3-5=10
  
• 
  m (К3) = m (В) - m (К2) - m (К6) - m (К5) = 18-2-4-5=7
  
• 
  m (К7) = m (С) - m (К4) - m (К6) - m (К5) = 18-3-4-5 =6
  
• 
  m (К2) + m (К4) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
  
• 
  m (К1) + m (К3) + m (К7) = 10+7+6=23 – число учеников решивших только одну задачу.
  

Ответ:

5 учеников решили три задачи;

9 учеников решили только по две задачи;

23 ученика решили только по одной задаче.

С помощью этого метода можно записать решения второй и третьей задачи так:

Решение задачи № 2

• 
  m (А В) = 33
  
• 
  m (А С) = 31
  
• 
  m (В С) = 32
  
• 
  m (К2) + m (К4) + m (К6) + m (К5) = 20
  

Найти m (К1) + m (К3) + m (К7)

• 
  m (АUВ) = m (К1) + m (К2) + m (К3) + m (К4) + m (К5) + m (К6) = m (К1) + m (К3) + 20 = 33 =>
  
• 
  m (К1) + m (К3) = 33 – 20 = 13
  
• 
  m (АUС) = m (К1) + m (К4) + m (К2) + m (К5) + m (К6) + m (К7) = m (К1) + m (К7) + 20 = 31 =>
  
• 
  m (К1) + m (К7) = 31 – 20 = 11
  
• 
  m (ВUС) = m (К3) + m (К2) + m (К5) + m (К6) + m (К7) + m (К4) = m (К3) + m (К7) + 20 = 32 =>
  
• 
  m (К3) + m (К7) = 32 – 20 = 12
  
• 
  2m (К1) + m (К3) + m (К7) = 13+11=24
  
• 
  2m (К1) + 12 = 24
  
• 
  
  
• 
  m (К3)= 13-6=7
  
• 
  m (К7)=12-7=5
  
• 
  m (К1) + m (К3) + m (К7) = 6+7+5=18
  

Ответ:

Только одну контрольную работу решили 18 учеников.

Решение задачи № 3

• 
  m (Е) = 35
  
• 
  m (А∩В∩С)= m (К5) = 6
  
• 
  m (А∩В)= 15
  
• 
  m (А∩С)= 13
  
• 
  m (В∩С)= 9
  

Найти m (К1) + m (К3) + m (К7)

• 
  m (К2) = m (А∩В) - m (К5) = 15-6=9
  
• 
  m (К4) = m (А∩С) - m (К5) = 13-6=7
  
• 
  m (К6) = m (В∩С) - m (К5) = 9-6=3
  
• 
  m (К1) + m (К3) + m (К7) = m (Е) - m (К4) - m (К2) - m (К6) - m (К5) = 35-7-9-3-6=10
  

Ответ:

Только одним видом транспорта пользуется 10 учеников.