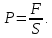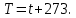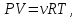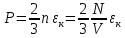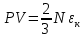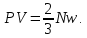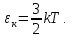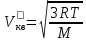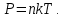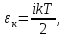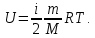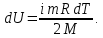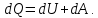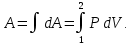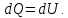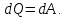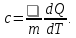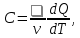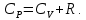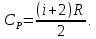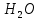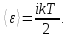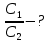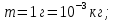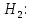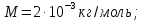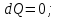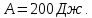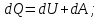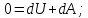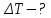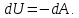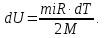Лекция по распределению максвелла. Молек физика и термод.-2 Упр по МФ и ТД-3 (2) (2). Молекулярная физика и термодинамика Основное уравнение мкт. Первое начало термодинамики
 Скачать 310.95 Kb. Скачать 310.95 Kb.
|
|
Молекулярная физика и термодинамика 1. Основное уравнение МКТ. Первое начало термодинамики План 1. Предмет молекулярной физики и термодинамики. Статистический и термодинамический методы 2. Идеальный газ. Уравнение Менделеева– Клапейрона. Газовые законы. 3. Основное уравнение МКТ 4.Число степеней свободы молекулы. Распределение энергии по степеням свободы. 5. Внутренняя энергия идеального газа. Работа и теплота. 1 начало термодинамики. 6. Теплоемкость. Уравнение Майера. 1. Предмет молекулярной физики и термодинамики. Статистический и термодинамический методы Молекулярная физика (МФ) изучает движение и взаимодействие огромного числа молекул, из которых состоят тела. В МФ используется статистический метод, который определяет средние значения характеристик молекул (микропараметры) (средняя скорость, средняя кинетическая энергия молекул и др.) В основе МФ лежит молекулярно-кинетическая теория (МКТ). Основные положения МКТ: 1. Все вещества состоят из частиц (молекул, атомов), между которыми есть промежутки. Явления, подтверждающие положение — диффузия, броуновское движение, конвекция. 2. Частицы находятся в непрерывном хаотичном(тепловом) движении Явления, подтверждающие положение — броуновское движение, конвекция, теплопроводность. 3. Частицы взаимодействуют друг с другом. Взаимодействие зависит от расстояния между частицами и характера сил. Явления, подтверждающие положение — теплопроводность. Термодинамика (ТД) изучает энергетические состояния тел и процессы обмена энергией между телами, не учитывая их молекулярного строения. Используется термодинамический метод, который определяет внутреннюю энергию, работу, теплоту, термодинамические параметры всего тела(системы) в целом. Термодинамические параметры — давление 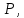 объем объем 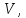 температура температура 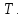 Давление 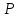 — сила давления, действующая на единицу площади. — сила давления, действующая на единицу площади.
Размерность в СИ: 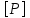 = Па. = Па.Объем 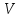 — область пространства, которое занимает тело. — область пространства, которое занимает тело.Размерность в СИ: 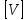 = м3. = м3.Температура 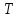 — мера нагретости тела, мера средней кинетической энергии молекул. — мера нагретости тела, мера средней кинетической энергии молекул.Размерность в СИ: 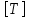 = К в термодинамической шкале. В практической шкале = К в термодинамической шкале. В практической шкале 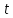 в ˚С. в ˚С.Связь 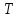 и и 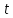 : :
Нормальные условия (н. у.): 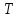 = 273 К (0˚С), = 273 К (0˚С), 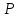 = 105 Па. = 105 Па.2. Идеальный газ. Уравнение Менделеева-Клапейрона. Газовые законы В МФ используется модель идеального газа. Идеальный газ — газ, в котором пренебрегают силами взаимодействия, размерами молекул. Из опыта известно, что газы атмосферы Земли (азот, кислород и др.) при невысоких давлениях (105–107 Па) и не очень низких температурах (Т много выше 0К) можно считать идеальными газами. Уравнение состояния идеального газа описывает уравнение Менделеева-Клапейрона:
где 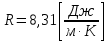 — универсальная газовая постоянная, — универсальная газовая постоянная, 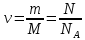 — количество вещества или число молей, — количество вещества или число молей, 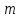 — масса газа, — масса газа, 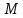 — молярная масса, — молярная масса, 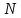 — число молекул в массе — число молекул в массе 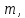 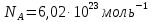 — число Авогадро. — число Авогадро.Уравнение устанавливает зависимость между основными термодинамическими параметрами — давлением, объемом и температурой газа. Из (3) можно получить уравнения для изопроцессов. Изопроцессы: 1) Изотермический: при 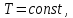 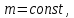 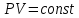 — закон Бойля–Мариотта. — закон Бойля–Мариотта.    2) Изобарный: при  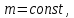 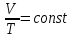 — закон Гей–Люссака. — закон Гей–Люссака.       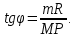 3) Изохорный: 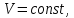 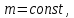 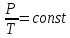 — закон Шарля. — закон Шарля. 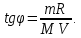 3. Основное уравнение МКТ Уравнение, связывающее макропараметры 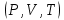 и микропараметры (средняя кинетическая энергия молекулы и микропараметры (средняя кинетическая энергия молекулы 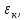 средняя квадратичная скорость средняя квадратичная скорость 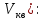
где 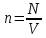 — концентрация молекул, — концентрация молекул, 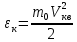 — средняя кинетическая энергия движения одной молекулы, — средняя кинетическая энергия движения одной молекулы, 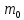 — масса одной молекулы, — масса одной молекулы,  — средняя квадратичная скорость: — средняя квадратичная скорость: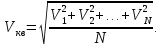 В некоторых источниках формула (4) записывается с использованием других обозначений: энергия молекулы 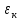 обозначается через обозначается через  а концентрация молекул а концентрация молекул  — через — через 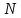 и и 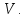
Мнемоническое правило: 2/3 всех молекул (N) С энергией дубль вэ (w) Давит (Р) на стенки сосуда Сосуд объемом вэ (V). Пользуясь уравнением (4) можно объяснить от чего зависит давление в молекулярно-кинетической теории: 1) 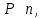 чем больше концентрация молекул, тем больше ударов молекул о стенки сосуда, тем больше результирующая сила давления, тем больше давление. чем больше концентрация молекул, тем больше ударов молекул о стенки сосуда, тем больше результирующая сила давления, тем больше давление.2) 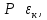 чем больше кинетическая энергия одной молекулы, тем больше сила удара одной молекулы о стенки сосуда, тем больше давление. чем больше кинетическая энергия одной молекулы, тем больше сила удара одной молекулы о стенки сосуда, тем больше давление.Следствия из основного уравнения МКТ газов 1) Так как левые части уравнений (4) и (3) равны (РV) , то приравняем правые части 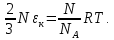 Сократив на 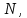 получим получим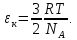 Так как 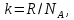 то средняя кинетическая энергия одной одноатомной молекулы то средняя кинетическая энергия одной одноатомной молекулы
При выводе формул (4), (4′) предполагалось, что молекулы одноатомные. 2) 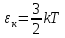 ; ; 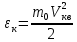 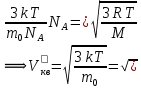
3) 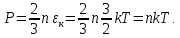
4.Число степеней свободы молекулы. Распределение энергии по степеням свободы Число степеней свободы молекулы (i) — количество независимых координат, полностью определяющих положение молекулы в пространстве. Зависит от числа атомов в молекуле и видов ее движения.  При поступательном движении вдоль каждой из осей (Х, Y, Z) положение молекулы изменяется, поэтому для характеристики положения молекулы имеется три поступательных степени свободы 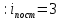 . При вращении вокруг любой из осей, проходящих через центр масс молекулы, положение ее не изменяется, поэтому вращательных степеней свободы нет: . При вращении вокруг любой из осей, проходящих через центр масс молекулы, положение ее не изменяется, поэтому вращательных степеней свободы нет: 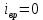  При поступательном движении вдоль каждой из осей (Х, Y, Z) положение молекулы как целого изменяется, поэтому для характеристики положения молекулы имеется три поступательных степени свободы 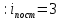 . При вращении вокруг оси, проходящей через оба атома молекулы (Х), положение ее атомов не изменяется, поэтому эта вращательная степень свободы 0. При вращении вокруг двух других осей (Y, Z) положение атомов в молекуле изменяется, что соответствует двум вращательным степеням свободы: . При вращении вокруг оси, проходящей через оба атома молекулы (Х), положение ее атомов не изменяется, поэтому эта вращательная степень свободы 0. При вращении вокруг двух других осей (Y, Z) положение атомов в молекуле изменяется, что соответствует двум вращательным степеням свободы: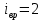 . Всего у двухатомной молекулы 5 степеней свободы. . Всего у двухатомной молекулы 5 степеней свободы. При поступательном движении вдоль каждой из осей (Х, Y, Z) положение молекулы как целого изменяется, поэтому для характеристики положения молекулы имеется три поступательных степени свободы 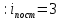 . При вращении вокруг каждой оси, положение двух ее атомов изменяется, поэтому вращательных степеней свободы 3: . При вращении вокруг каждой оси, положение двух ее атомов изменяется, поэтому вращательных степеней свободы 3: 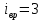 . Всего у многоатомной молекулы 6 степеней свободы. . Всего у многоатомной молекулы 6 степеней свободы.Для одноатомной молекулы 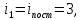 а ее средняя кинетическая энергия а ее средняя кинетическая энергия 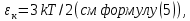 тогда на одну поступательную степень свободы приходится энергия тогда на одну поступательную степень свободы приходится энергия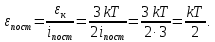 Какая энергия приходится на вращательную, колебательную степени свободы? 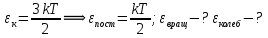 При хаотическом движении поступательное и вращательное движения равновероятны. Молекула может одновременно и вращаться и поступательно двигаться, поэтому кинетические энергии поступательного и вращательного движения должны быть равны. Энергия колебательного движения включает в себя как кинетическую, так и потенциальную энергию колебательного движения. Поэтому энергия колебательного движения должна быть в 2 раза больше энергии поступательного или вращательного движения. В классической термодинамике принят следующий закон: Закон равномерного распределения энергии по степеням свободы В системе, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степень свободы приходится одинаковая энергия, равная 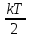 , а на колебательную степень свободы — энергия, равная , а на колебательную степень свободы — энергия, равная 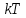 . .Если молекула имеет 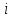 степеней свободы, то средняя кинетическая энергия одной молекулы с степеней свободы, то средняя кинетическая энергия одной молекулы с 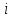 степенями свободы равна степенями свободы равна
где 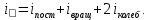 5. Внутренняя энергия идеального газа. Работа и теплота. Первое начало термодинамики Внутренняя энергия газа — это кинетическая энергия движения его молекул и потенциальная энергия их взаимодействия. В идеальном газе пренебрегают силами взаимодействия, следовательно, потенциальная энергия взаимодействия равна 0: 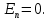 Тогда внутренняя энергия идеального газа равна только кинетической энергии его молекул Тогда внутренняя энергия идеального газа равна только кинетической энергии его молекул 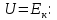 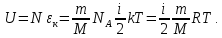
При изменении температуры на 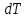 произойдет изменение внутренней энергии произойдет изменение внутренней энергии
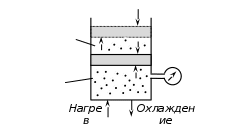
При неизменной массе газа внутренняя энергия может меняться в результате двух процессов: совершение работы (газом или над газом) и передача теплоты (от газа к окружающим телам или наоборот). Работа и теплота – два вида передачи энергии, между которыми есть принципиальные различия. Работа  - такой вид передачи энергии, при котором поступательное движение 1-го тела переходит в поступательное движение 2-го тела. Пример: газ в цилиндре с подвижным поршнем При нагревании дна цилиндра газ расширяется в направлении поршня, т.е. газ( 1 тело) поступательно движется в направлении поршня (тело 2),под действием газа поршень начинает двигаться поступательно. Теплота - такой вид передачи энергии, при котором поступательное движение 1-го тела переходит в поступательное движение 2-го тела. Пример: газ в цилиндре с подвижным поршнем При нагревании дна цилиндра газ расширяется в направлении поршня, т.е. газ( 1 тело) поступательно движется в направлении поршня (тело 2),под действием газа поршень начинает двигаться поступательно. Теплота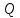 - такой вид передачи энергии, при котором хаотическое тепловое движение 1-го тела переходит в хаотическое тепловое движение 2-го тела. Пример: кастрюля стоит на электрической плите. Плиту включают, молекулы плиты( 1 тело) начинают более интенсивно хаотично двигаться, сталкиваясь с молекулами кастрюли (тело 2), передают им свою кинетическую энергию, и молекулы кастрюли тоже начинают быстрее двигаться хаотично. - такой вид передачи энергии, при котором хаотическое тепловое движение 1-го тела переходит в хаотическое тепловое движение 2-го тела. Пример: кастрюля стоит на электрической плите. Плиту включают, молекулы плиты( 1 тело) начинают более интенсивно хаотично двигаться, сталкиваясь с молекулами кастрюли (тело 2), передают им свою кинетическую энергию, и молекулы кастрюли тоже начинают быстрее двигаться хаотично. Первое начало термодинамики: 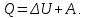 При бесконечно малом нагревании(охлаждении)
Количество теплоты 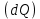 , подводимое к системе, расходуется на изменение внутренней энергии этой системы , подводимое к системе, расходуется на изменение внутренней энергии этой системы 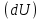 и на совершение этой системой работы над внешними телами и на совершение этой системой работы над внешними телами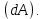 Если система (тело ) само совершает работу, то работа положительна, и в (11) знак «+». Если над системой(телом) совершают работу, то работа отрицательна, и в (11) знак «-». Посчитаем работу газа при расширении: Пусть в результате нагревания газа поршень поднялся под действием силы давления 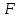 на на 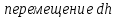 . Тогда работа силы давления . Тогда работа силы давления 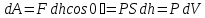 При выводе учитывается , что перемещение происходит в направлении действия силы, поэтому угол  , , 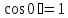 ,сила давления ,сила давления 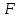 выражается из формулы(1), произведение площади поршня выражается из формулы(1), произведение площади поршня 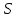 и перемещения и перемещения 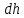 дает объем цилиндра дает объем цилиндра 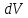 При любом изменении объема от V1 до V2 совершается работа:
Геометрический смысл интеграла (12): работа газа А - площадь фигуры, ограниченной кривой Р(V), осью абсцисс, прямыми V=V1 и V=V2  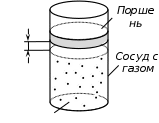 Применение первого начала термодинамики к изопроцессам и адиабатному процессу 1) Изохорный процесс: 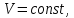 следовательно, следовательно, 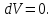 Как осуществить процесс? Как осуществить процесс?Цилиндр с газом закрыт поршнем, который закрепляют, чтобы объем не изменялся. Газ нагревают (охлаждают), температура изменяется на 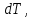 а значит, согласно уравнению (10), его внутренняя энергия изменится на а значит, согласно уравнению (10), его внутренняя энергия изменится на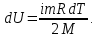 Работа при этом равна 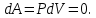 Тогда из первого начала термодинамики 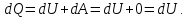 Первое начало термодинамики при изохорном процессе:
Всё тепло, сообщаемое телу, идет только на изменение его внутренней энергии. 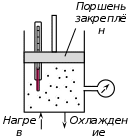 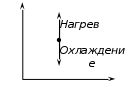 2) Изобарный процесс: 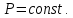 Как осуществить процесс? Как осуществить процесс?Цилиндр с газом закрыт поршнем, который может свободно перемещаться. Сначала газ занимает объем 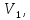 при этом давление газа под поршнем при этом давление газа под поршнем 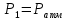 — атмосферному давлению над поршнем. После нагрева (охлаждения) цилиндра с газом на — атмосферному давлению над поршнем. После нагрева (охлаждения) цилиндра с газом на 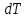 газ начнет расширяться (сжиматься), поршень будет перемещаться, но до тех пор, пока давление под поршнем снова не станет равным атмосферному: газ начнет расширяться (сжиматься), поршень будет перемещаться, но до тех пор, пока давление под поршнем снова не станет равным атмосферному: 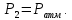 При этом объем газа изменится на При этом объем газа изменится на 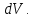 В этом процессе из-за изменения температуры внутренняя энергия изменяется на В этом процессе из-за изменения температуры внутренняя энергия изменяется на 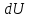 и из-за изменения объема совершается работа и из-за изменения объема совершается работа 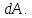 Поэтому первое начало термодинамики при изобарном процессе записывается как Поэтому первое начало термодинамики при изобарном процессе записывается как
  3) Изотермический процесс: 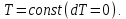 Как осуществить процесс? Как осуществить процесс?Цилиндр с газом закрыт поршнем, который может свободно перемещаться. Будем медленно перемещать поршень, чтобы успевал происходить теплообмен с окружающей средой, тогда температура изменяться не будет. Значит и внутренняя энергия не будет изменяться, из (10) следует 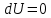 и и 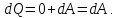 Первое начало термодинамики при изотермическом процессе:
Работа при расширении (сжатии) газа равна теплу, которое передается газу (отводится от газа) в результате теплообмена с окружающей средой.   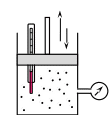 Поршень медленно поднимается или опускается Получим выражение для работы при изотермическом процессе: Для этого из уравнения Менделеева -Клапейрона (3) выразим Р= 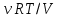 и подставим в (12): и подставим в (12):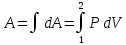 = =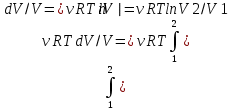 Учитывая, что 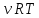 не изменяется в данном процессе, можно вынести за знак интеграла. Вычисление интеграла дает натуральный логарифм объема V, который в пределах от V1 до V2 равен разности логарифмов lnV2 - lnV1=lnV2 / V1 не изменяется в данном процессе, можно вынести за знак интеграла. Вычисление интеграла дает натуральный логарифм объема V, который в пределах от V1 до V2 равен разности логарифмов lnV2 - lnV1=lnV2 / V14) Адиабатный процесс - процесс, происходящий без теплообмена ( 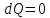 ). ).Как осуществить процесс? Аналогично изотермическому, но поршень нужно перемещать быстро, чтобы не успевал происходить теплообмен. Цилиндр с газом закрыт поршнем, который может свободно перемещаться. Будем быстро перемещать поршень, чтобы не успевал происходить теплообмен с окружающей средой, тогда будут изменяться и температура, и давление, и объем. Значит из (10) внутренняя энергия будет изменяться 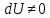 и совершится работа и совершится работа 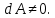 Тогда из (11) Тогда из (11)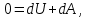 откуда 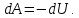 Первое начало термодинамики при адиабатном процессе:
Работа, совершаемая газом, приводит к уменьшению его внутренней энергии, работа над газом приводит к увеличению его внутренней энергии. Пример адиабатического процесса: при быстром накачивании колеса воздухом (адиабатное сжатие газа) температура газа в баллоне становится выше, чем в окружающей среде; при быстром выходе газа из проткнутого колеса (адиабатное расширение) температура оставшегося в баллоне газа ниже, чем в окружающей среде. Объясняется это тем, что в первом случае число молекул увеличивается, они приносят с собой кинетическую энергию хаотического теплового движения, которая является внутренней энергией идеального газа, а значит температура газа увеличивается. Во втором случае число молекул уменьшается, они уносят с собой кинетическую энергию, внутренняя энергия уменьшается, и температура понижается.    Поршень быстро поднимается или опускается Графики изотермы и адиабаты похожи (гиперболы), но зависимость 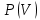 адиабаты более крутая, чем изотермы, т.к. уравнение изотермы адиабаты более крутая, чем изотермы, т.к. уравнение изотермы 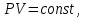 а у адиабаты а у адиабаты 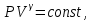 где где 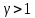 , показатель адиабаты , показатель адиабаты 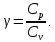 6. Теплоемкость. Уравнение Майера Одной из характеристик тепловых свойств тел является теплоемкость. Удельная теплоемкость с — тепло, которое необходимо для нагрева на один градус единицы массы вещества (малая буква с).
Размерность в СИ: 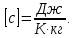 Молярная теплоемкость 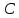 — тепло, которое необходимо для нагрева на один градус одного моля вещества (большая буква — тепло, которое необходимо для нагрева на один градус одного моля вещества (большая буква 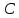 ). ).
где 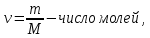 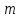 — масса вещества, — масса вещества, 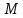 — молярная масса. — молярная масса.Размерность в СИ: 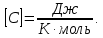 Используя (13) и (10), получим теплоемкость при постоянном объеме: 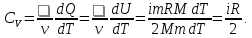
Используя (14), (19), (12) и уравнение Менделеева-Клапейрона, получим теплоемкость при постоянном давлении: 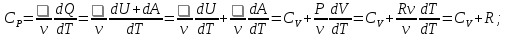
Формула (20) — это уравнение Майера, оно устанавливает связь теплоемкостей при постоянном давлении и постоянном объеме. Учитывая (19), 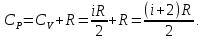
Из уравнения (20) видно, что 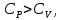 и их отношение-показатель адиабаты и их отношение-показатель адиабаты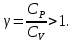 Выводы: 1. Существуют два метода изучения вещества: статистический — изучает вещества на микроуровне (определяет средние скорости и энергии молекул системы) и термодинамический — изучает вещества на макроуровне (определяет энергетические состояния и переходы между ними системы как целого). 2. Основное уравнение МКТ устанавливает связь между макропараметрами 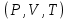 и микропараметрами (средняя квадратичная скорость, кинетическая энергия молекул и микропараметрами (средняя квадратичная скорость, кинетическая энергия молекул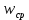 , масса одной молекулы): , масса одной молекулы): 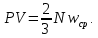 3. Теплоемкость вещества зависит от процесса его нагревания: 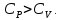 Задачи по теме «Молекулярная физика. Первое начало термодинамики» 1. Средняя кинетическая энергия молекул газа при температуре 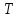 зависит от их структуры, что связано с возможностью участвовать в различных видах движения атомов и молекул (поступательное, вращательное, колебательное). Чему равна средняя кинетическая энергия молекул водяного пара, если не учитывать колебательное движение молекул? Энергию выразить через зависит от их структуры, что связано с возможностью участвовать в различных видах движения атомов и молекул (поступательное, вращательное, колебательное). Чему равна средняя кинетическая энергия молекул водяного пара, если не учитывать колебательное движение молекул? Энергию выразить через 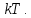
3. Из условия известно, что молекулы пара трёхатомные, следовательно, поступательные степени свободы 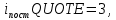 вращательные 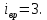 Всего степеней свободы 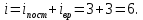 4. Тогда 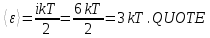 2. Молярные теплоемкости азота  в процессах 1-2 и 1-3 равны в процессах 1-2 и 1-3 равны  и и 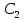 соответственно. Чему равно отношение соответственно. Чему равно отношение 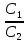 ? ?
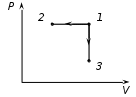
1. Физические явления: изобарный и изохорный процессы идеальных газов. 2. Молярные теплоемкости, выраженные через степени свободы 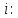 – при постоянном давлении 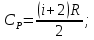 – при постоянном объеме 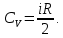 3. Из графика видно, что процесс 1–2 изобарный, следовательно, 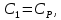 процесс 1–3 изохорный, следовательно, процесс 1–3 изохорный, следовательно, 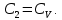 Тогда Тогда 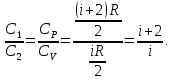 4. Молекула азота состоит из двух атомов, следовательно, 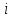 = 5. = 5.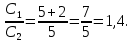 3. На 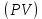 -диаграмме изображены два циклических процесса. Определить отношение работ -диаграмме изображены два циклических процесса. Определить отношение работ 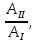 совершенных в этих циклах. совершенных в этих циклах.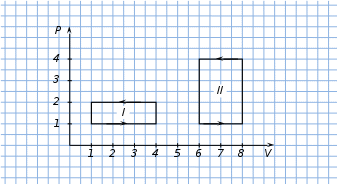 1. Физические явления: циклы. 2. Работа в термодинамике: 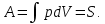 Геометрический смысл этого интеграла — площадь фигуры  ограниченной графиком функции ограниченной графиком функции  и прямыми и прямыми 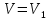 и и 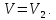 Можно показать, что работа цикла равна площади самого цикла: Можно показать, что работа цикла равна площади самого цикла: 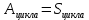 . . 3. Площадь цикла I — площадь прямоугольника 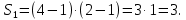 Площадь цикла II –площадь прямоугольника 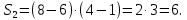 4. Находим искомое отношение: 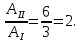 4. Один грамм водорода, расширяясь адиабатически, совершил работу 200 Дж. Какое изменение температуры по модулю произошло в этом процессе?
Из (2) выразим: 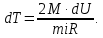 3. По условию из (1) выразим изменение внутренней энергии по модулю 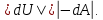 Тогда изменение температуры по модулю 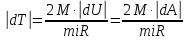 или 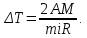 4. Для двухатомной молекулы 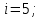 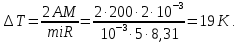 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||