ОтчётЛБ1КомягинМ.А.. Московский авиационный институт
 Скачать 169.78 Kb. Скачать 169.78 Kb.
|
|
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) Кафедра 610 Управление эксплуатацией ракетно-космических систем Отчёт По лабораторной работе №1 «Расчёт показателей безотказности невосстанавливаемых систем» Вариант №19 Составил: студент гр. М6О-413С Комягин М.А Проверил: преподаватель Коробовский Александр Валентинович Задача 1. На испытании находилось N0 = 2500 образцов неремонтируемой аппаратуры. Число отказов 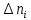 фиксировалось каждые фиксировалось каждые 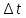 часов. Продолжительность испытаний Tи составила 3000 часов. Данные об отказах представлены в таблице 1, где N соответствует выданному варианту, N=19. часов. Продолжительность испытаний Tи составила 3000 часов. Данные об отказах представлены в таблице 1, где N соответствует выданному варианту, N=19.Таблица 1, исходные данные
В ходе выполнения задачи 1, с помощью программы MATLAB были построены графики статистических оценок интенсивности отказов λ(t), частоты отказов f(t), вероятности безотказной работы P(t) и вероятности отказов Q(t). Первым этапом в решении задачи стал расчёт вероятности безотказной работы P(t) по формуле (1): 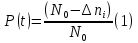 Ниже представлены полученные значения для P(100), P(200) и P(3000): 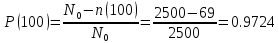 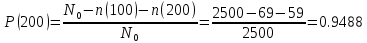 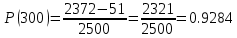 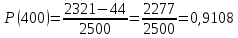 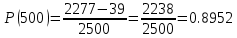 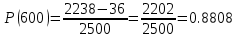 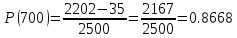 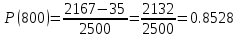 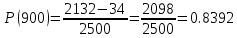 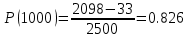 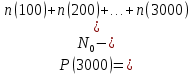 P(1800) = 0.7216 P(1900) = 0.7084 P(2000) = 0.6960 P(2100) = 0.6836 P(2200) = 0.6708 P(2300) = 0.6584 P(2400) = 0.6456 P(2500) = 0.6324 P(2600) = 0.6184 P(2700) = 0.6028 P(2800) = 0.5852 P(2900) = 0.5656 P(3000) = 0.5420 По полученным значениям были построены гистограмма и график зависимости вероятности безотказной работы P(t) от времени t, ч. Результат построения представлены на рис.1 и рис.2. 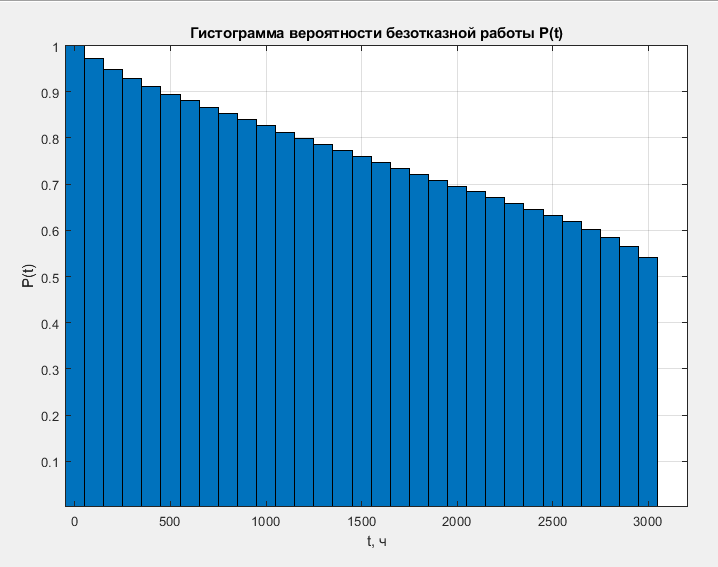 Рисунок 1, гистограмма вероятности безотказной работы P(t) 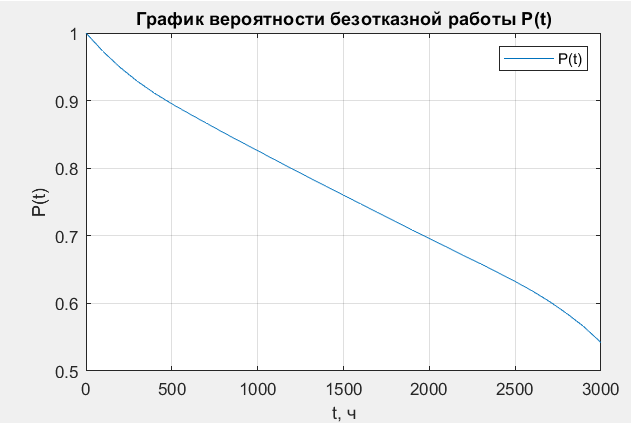 Рисунок 2, график вероятности безотказной работы P(t) Затем, по формуле (2) были определена вероятность отказа Q(t): 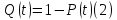 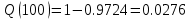 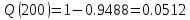 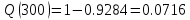 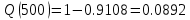 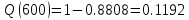 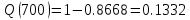 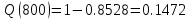 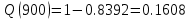 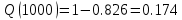 Ниже, в таблице 2 представлены полученные значения. Также по ним были построены гистограмма и график (рис.3 и рис.4 соответственно) зависимости вероятности отказов Q(t) от времени t.
Таблица 2, рассчитанные значения вероятностей отказов 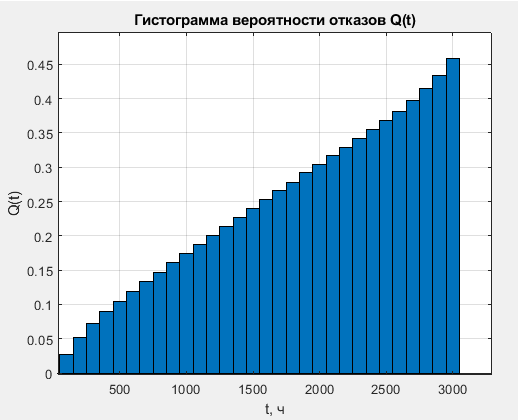 Рисунок 3, гистограмма вероятностей отказов 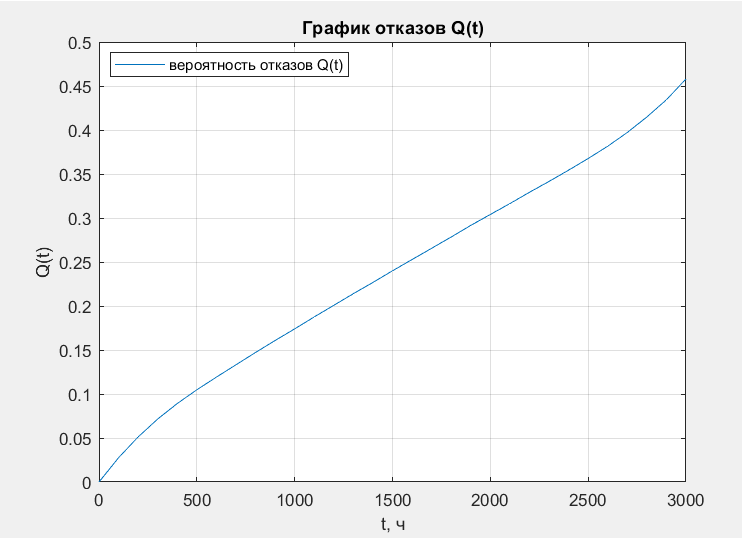 Рисунок 4, график вероятностей отказов Q(t) Далее, по формуле (3) была определена частота отказов f(t): 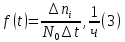 Так, 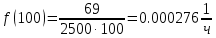 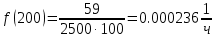 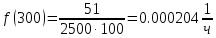 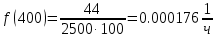 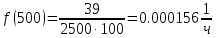 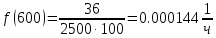 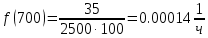 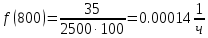 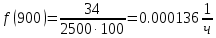 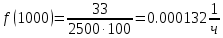 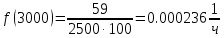 Полученные результаты представлены в таблице 3.
Таблица 3, рассчитанные значения частоты отказов f(t), 1/ч По полученным результатам был построен график и гистограмма зависимости частоты отказов f(t) от времени t (рис.5 и 6 соответственно). 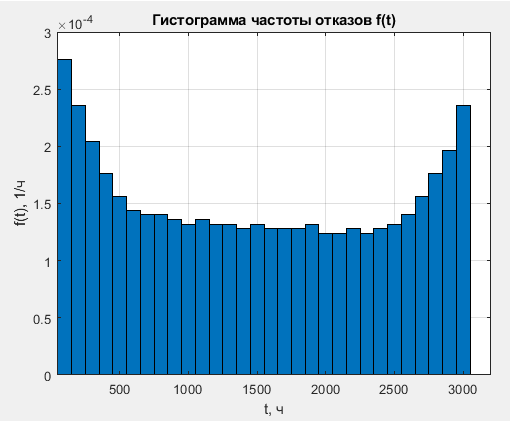 Рисунок 5, гистограмма зависимости частоты отказов f(t) от времени t 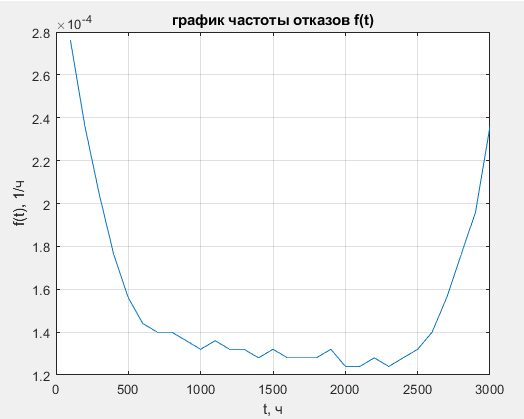 Рисунок 6, график зависимости частоты отказов f(t) от времени t На последнем этапе выполнения задачи 1 была вычислена интенсивность отказов λ(t). Для вычислений была использована формула (4): 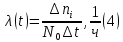 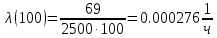 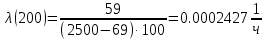 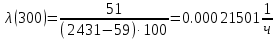 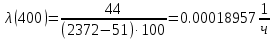 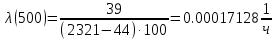 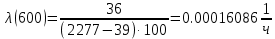 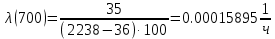 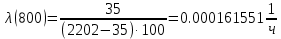 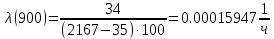 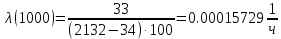 Все полученные результаты вычислений представлены в таблице 4.
Таблица 4, рассчитанные значения интенсивности отказов 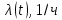  По полученным данным были построены гистограмма и график зависимости отказов 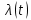 от времени t (рис.7 и 8). от времени t (рис.7 и 8).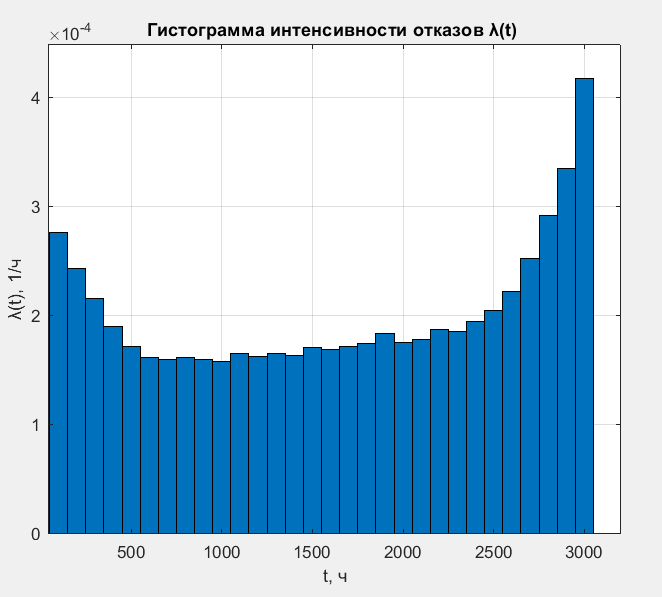 Рисунок 7, гистограмма зависимости интенсивности отказов 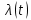 от времени t от времени t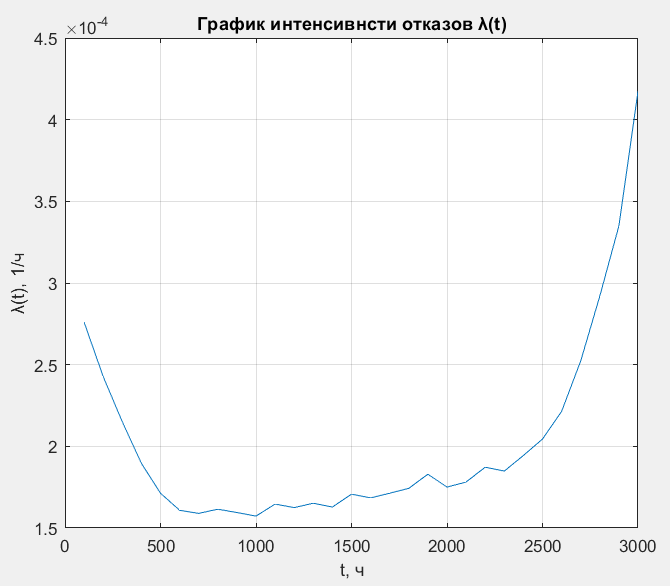 Рисунок 8, график зависимости интенсивности отказов λ(t) от времени t Задание 2 Для условия задачи 1 вычислить также значение средней наработки до отказа в предположении, что: А) на испытании находились только отказавшие образцы Б) на испытании находились все 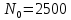 образцов образцовЗакон распределения наработки до отказа экспоненциальный. А) Для решения задачи были использовано соотношение (5) и 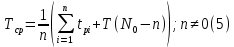 Число отказов n=1145, 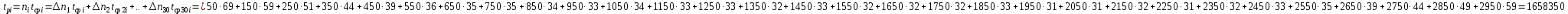 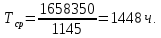 Б) Подставив известные данные в выражение (5) получим: 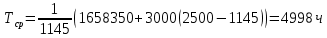 Задание 3 Используя функцию надежности, полученную по результатам задачи 1, оценить, какова вероятность того, что СТС, проработавшей безотказно в интервале (0, 300) часов, не откажет в течение интервала (300, 600) часов. Рассчитаем по выражению (6) условную вероятность безотказной работы: 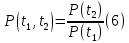 Тогда вероятность безотказной работы в интервале от 300 до 600 ч составит: 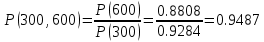 Москва 2020 |

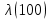 , 1/ч
, 1/ч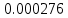
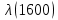 , 1/ч
, 1/ч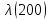 , 1/ч
, 1/ч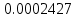
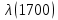 , 1/ч
, 1/ч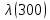 , 1/ч
, 1/ч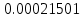
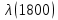 , 1/ч
, 1/ч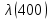 , 1/ч
, 1/ч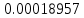
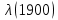 , 1/ч
, 1/ч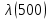 , 1/ч
, 1/ч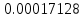
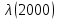 , 1/ч
, 1/ч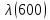 , 1/ч
, 1/ч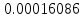
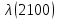 , 1/ч
, 1/ч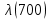 , 1/ч
, 1/ч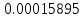
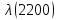 , 1/ч
, 1/ч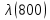 , 1/ч
, 1/ч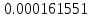
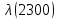 , 1/ч
, 1/ч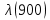 , 1/ч
, 1/ч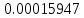
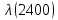 , 1/ч
, 1/ч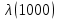 , 1/ч
, 1/ч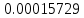
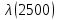 , 1/ч
, 1/ч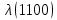 , 1/ч
, 1/ч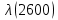 , 1/ч
, 1/ч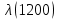 , 1/ч
, 1/ч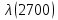 , 1/ч
, 1/ч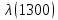 , 1/ч
, 1/ч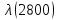 , 1/ч
, 1/ч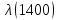 , 1/ч
, 1/ч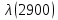 , 1/ч
, 1/ч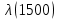 , 1/ч
, 1/ч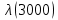 , 1/ч
, 1/ч