Основы теории надежности вар. Основы теории надежности 7. Основы теории надежности Контрольная работа
 Скачать 27.39 Kb. Скачать 27.39 Kb.
|
|
Основы теории надежности Контрольная работа Вариант 7 Построить функцию надежности изделия, время безотказной работы которого подчиняется экспоненциальному закону распределения. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение. Исходные данные: интенсивность отказов λ = 0,1 1/ч. Решение: Непрерывная случайная величина имеет показательный (экспоненциальный) закон распределения с параметром λ >0, если ее плотность вероятности имеет вид: 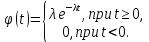 Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению. Как видно из формулы , показательное распределение определяется только одним параметром λ. Найдем функцию распределения показательного закона, используя свойства дифференциальной функции распределения: 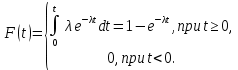 Функция надежности изделия Q(t)=1-F(t), время безотказной работы которого подчиняется экспоненциальному закону распределения построена с помощью программы MATHCAD и приведена на рис. 1. Математическое ожидание: 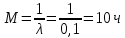 . .Дисперсия: 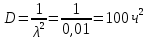 . .Среднее квадратическое отклонение: 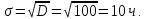 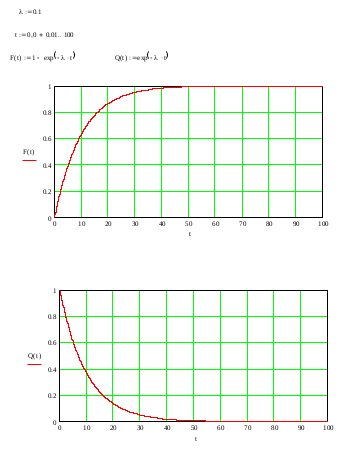  Рис. 1. Рис. 1. |
