Основные понятия и определения теории надежности
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ НАДЕЖНОСТИ. В теории надежности существует единая терминология, которая изложена в стандартах (ГОСТах). К 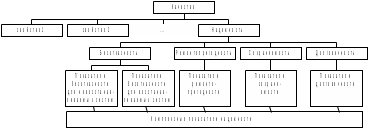 ачество - совокупность свойств продукции, которая позволяет оценить пригодность продукции удовлетворять определенным потребностям в соответствии с её назначением. Одним из качеств изделия является надежность - особое свойство, которое позволяет определить стабильность всех других свойств качества изделия во времени. Свойство - объективная особенность изделия, которое проявляется при его создании, эксплуатации и потреблении. Надежность системы (ГОСТа 27.002-89) - свойство системы выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки. Исправное состояние - состояние, при котором система обладает полным набором свойств и выполняет все заданные функции с параметрами, установленными в технической документации. Работоспособность - состояние, при котором система выполняет все заданные функции с параметрами, установленными требованиями технической документации, но с отсутствием некоторых несущественных для нормального функционирования свойств. Отказ - событие, которое заключается в нарушении работоспособности. Под отказом надо понимать не только полное нарушение работоспособности, но и выход параметров изделия за границы, установленные требованиями технической документации. После отказа система либо полностью прекращает свою работу, либо продолжает функционировать с пониженным качеством. ИС – это сложная программно-аппаратная система, включающая в свой состав эргатические (человеко-машинные) звенья, технические или аппаратные средства и программное обеспечение. Основные понятия. Термины и определения" [2], формулирующий применяемые в науке и технике термины и определения в области надёжности, и материалы сайта [3]. под надёжностью понимают свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки. ПОНЯТИЕ ОТКАЗА. КЛАССИФИКАЦИЯ ОТКАЗОВ. Отказ является событием нарушения работоспособности и происходит в результате воздействия на ТУ различных агрессивных факторов, по большей части носящих случайный характер. Таким образом, отказ является случайным событием со всеми особенностями, присущими случайному событию. При переходе объекта в различные состояния могут возникнуть также повреждения – события, заключающиеся, в отличие от отказа, в нарушении исправности объекта при сохранении его работоспособности. Выделяется понятие критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт отказа. Отказ - событие, которое заключается в нарушении работоспособности. Под отказом надо понимать не только полное нарушение работоспособности, но и выход параметров изделия за границы, установленные требованиями технической документации. После отказа система либо полностью прекращает свою работу, либо продолжает функционировать с пониженным качеством. По характеру возникновения: Внезапные (катастрофические). Возникают в результате резкого (скачкообразного) изменения выходных показателей системы; Постепенные (параметрические). Образуются при постепенном снижении выходных параметров системы во времени и когда эти параметры пересекают критическое значение, считается, что отказ произошел. По степени очевидности: Явные (очевидные). Явные отказы системы обнаруживаются при внешнем осмотре или включении системы; Скрытые (неочевидные). Выявляются инструментальными средствами. По связи с отказами других элементов: Зависимые (вторичные отказы). Возникают под влиянием отказов других элементов; Независимые (первичные отказы). По времени существования: Устойчивые (окончательные). Устраняются только в результате ремонта; Перемежающие отказы (самопроизвольно возникают и устраняются). Исчезают без вмешательства обслуживающего персонала (например, сбои ЭВМ). По влиянию на ремонтопригодность: Неисправности. Устраняются путем мелкого ремонта; Аварии. Требуют длительного восстановления и больших ремонтных работ. По природе возникновения: Физические. Проявляются в физическом нарушении работоспособности; Функциональные. Теряют способность системы выполнять некоторые или все функции (например, при отсутствии физического отказа ЭВМ может неправильно выполнять логические операции). СВОЙСТВА НАДЕЖНОСТИ ЭИС. ОСНОВНЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ И ИХ ХАРАКТЕРИСТИКА. Надежность системы (ГОСТа 27.002-89) - свойство системы выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки. Надежность является комплексным свойством системы и включает в себя 4 свойства: 1. Безотказность - свойство системы не утрачивать работоспособность в течение заданной наработки без перерывов 2. Долговечность - свойство системы сохранять работоспособность до предельного состояния (до списания) с перерывами на техническое обслуживание и ремонт. 3. Ремонтопригодность - свойство системы обнаруживать, устранять и предупреждать неисправность и отказы путем проведения технического обслуживания и ремонта. 4. Сохраняемость - свойство системы сберегать свои эксплуатационные показатели в течение и после срока транспортирования или хранения на складе. 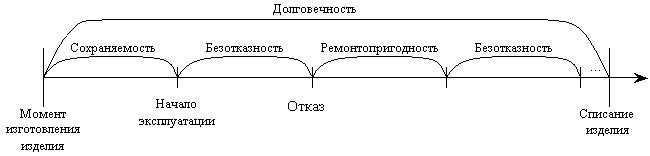 Показатели надежности и их характеристика. Количественные показатели случайных величин, которые могут характеризовать свойства безотказности, ремонтопригодности, сохраняемости и долговечности. В качестве единиц измерения применяются: - для безотказности - непрерывное время безотказной работы системы (наработка на отказ T’); - для долговечности - время от момента изготовления системы до предельного состояния или списания. (срок службы T’’); - для ремонтнопригодности - время восстановления работоспособности T’’’; - для сохраняемости - случайное время сохранения работоспособности в состоянии хранения “T”. Случайные величины, позволяют количественно оценить путем применения математического аппарата теории вероятностей и математической статистики. Полной характеристикой любой случайной величины является закон ее распределения, используемый в двух видах: как функция распределения (интегральный закон) и как плотность распределения (дифференциальный закон). Функцией распределения называется функция F(t), определяющая вероятность того, что случайная величина Т примет значение, меньшее заданной величины t, т.е.:  . .Плотностью распределения вероятностей непрерывной случайной величины Т в диапазоне от 0 до бесконечности называют функцию f ( t ) - первую производную от функции распределения F ( t ):  . .В теории надежности широко используются еще две функции: обратная функция распределения:  интенсивность: 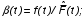 Рассмотрим графики этих функций.(рис. 1.3-1.6).
Рис.1.3. График функции 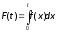 Рис.1.4. График функции Рис.1.4. График функции 
Рис. 1.4. График функции 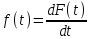 Рис.1.5. График функции Рис.1.5. График функции 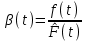 Зависимость между функциями b(t) и 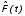 можно определить из соотношений: можно определить из соотношений:  , (1.2.5) , (1.2.5) . (1.2.6) . (1.2.6)Подставим выражение (1.2.6) в (1.2.5): 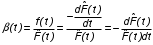 . .Проинтегрируем обе части выражения:  Таким образом, получаем зависимость 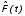 от (t): от (t):  . .КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА НАДЕЖНОСТИ. Методы расчета надежности сложных информационных систем применяются на этапе проектирования. Они относятся к схемно-конструкторским методам. Суть этих методов сводится к тому, что при известных показателях надежности отдельных элементов необходимо рассчитать надежность системы. К классическим методам относятся модели надежности с 1) последовательным, 2) параллельным, 3) параллельно-последовательным соединениями элементов, их различные модификации. 1) Модель с последовательным соединением элементов. При расчетах надежности последовательным называется такое соединение элементов, при котором отказ хотя бы одного из них приводит к отказу всего соединения в целом. Последовательное соединение не всегда совпадает с физическим последовательным соединением элементов. Отказы элементов предполагаются независимыми, то есть отказ любой группы элементов никак не влияет на вероятностные характеристики остальных элементов. Элемент понимается как один из самостоятельных участков последовательного соединения.  В данном случае вероятность безотказной работы системы можно рассчитать по формуле:  где Рс – вероятность безотказной работы системы; Рi(t) – вероятность безотказной работы i-го элемента системы. 2) Модель с параллельным соединением элементов. При расчетах надежности параллельным (резервным) называется такое соединение элементов, при котором отказ всего соединения происходит при отказе всех элементов системы (элементы дублируют друг друга). 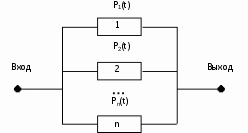 В этом случае показатель надежности системы Pc определяется через вероятности отказа элементов q1, q2, …, qn, которые связаны с вероятностью безотказной работы соотношениями вида qi(t) = 1 – Pi(t) Вероятность отказа всей системы равна: 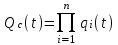 Тогда вероятность безотказной работы системы с параллельным соединением элементов q1, q2, …, qn имеет вид .  3) Модель с параллельно-последовательным соединением элементов. При расчетах надежности параллельно-последовательным называется такое соединение элементов, при котором можно составить структурные схемы участков как с последовательным, так и с паралелльным соединением элементов. 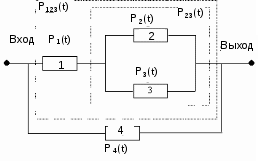 Для системы вначале рассчитывается вероятность безотказной работы участка 23: P23 = 1 - (1 - P2(t))(1 – P3(t)), затем – участка 123: P123(t) = P1(t)P23(t) = P1(t)(1 – (1 – P2(t))(1 – P3(t))) Итоговая расчетная формула имеет вид Pс(t) = 1 – (1 – P123(t))(1 – P4(t)). ЛОГИКО - ВЕРОЯТНОСТНЫЙ МЕТОД РАСЧЕТА НАДЕЖНОСТИ СИСТЕМ. Метод основан на математическом аппарате алгебры логики. Расчет надежности системы управления предполагает определение связи между сложным событием (отказ системы) и событиями, от которых оно зависит (отказы элементов системы). Следовательно, расчеты на надежность основаны на проведении операций с событиями и высказываниями, в качестве которых принимаются утверждения о работоспособности или отказе элемента (системы). Каждый элемент системы представляется логической переменной, принимающей значение 1 или 0. События и высказывания при помощи операций дизъюнкции, конъюнкции и отрицания объединяются в логические уравнения, соответствующие условию работоспособности системы. Составляется логическая функция работоспособности. Расчет, основанный на непосредственном использовании логических уравнений, называется логико-вероятностным и выполняется в семь этапов: 1. Словесная формулировка условий работоспособности объекта. Описывается зависимость работоспособности информационной системы от состояния ее отдельных элементов. 2. Составление логической функции работоспособности. Представляет собой логическое уравнение, соответствующее условию работоспособности системы управления  , (2.2) , (2.2)которое выражено в дизъюнктивной форме, например:  , ,где xi – условие работоспособности i-го элемента Fл; Xi = 1 – работоспособное состояние, Xi = 0 – неработоспособное состояние. 3. Приведение логической функции работоспособности FЛ к ортогональной бесповторной форме FЛО. Сложную логическую функцию работоспособности необходимо привести к ортогональной бесповторной форме. Функция вида (2.2) называется ортогональной, если все ее члены Di попарно ортогональны (то есть, их произведение равно нулю), и бесповторной, если каждый ее член Di состоит из букв хi, с разными номерами (то есть отсутствуют повторяющиеся аргументы), например: произведение элементарных конъюнкций х1, х2, x4 и х3, x2 равно нулю, так как одна из них содержит x2, а другая – x2, следовательно, они ортогональны; D1 = x1x2x2, где x2 и x2 имеют один и тот же номер, поэтому член D1 не является бесповторным.  – ортогональная бесповторная форма; – ортогональная бесповторная форма;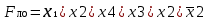 – ортогональная, но не бесповторная форма. – ортогональная, но не бесповторная форма. Функцию Fл можно преобразовать к ортогональной бесповторной форме Fло, используя законы и правила преобразования сложных высказываний. При расчетах наиболее употребительны правила: x1x2 = x2x1;  ; ; ; ; ; ;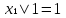 ; ;x11 = 1;  ; ;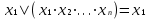 ; ;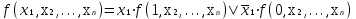 . . 4. Арифметизация Fло. По найденной ортогональной бесповторной логической функции работоспособности FЛО определяется арифметическая функция Fa (2.3). 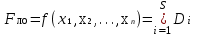  (2.3) (2.3)где Ai – арифметическая форма членов Di функции Fло. Арифметизация членов Di, в общем виде содержащих операции дизъюнкции, конъюнкции и отрицания, осуществляется заменой логических операций арифметическими по правилам:  ; ; 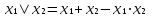 ; ;  . . 5. Определение вероятности безотказной работы системы. Вероятность безотказной работы системы устанавливается как вероятность истинности логической функции работоспособности, представленной в ортогональной бесповторной форме, и вычисляется как сумма вероятностей истинности всех ортогональных членов этой функции алгебры логики. Все события (высказывания) заменяются их вероятностями (вероятностями безотказной работы соответствующих элементов). 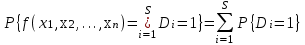 6. Вычисление требуемых показателей надежности системы управления по найденному показателю Pc(t): вероятность безотказной работы Pc(t); вероятность отказа Qc(t) = 1 – Pc(t); интенсивность отказов  ; ; средняя наработка до отказа 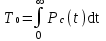 ; ; 7. Анализ соответствия полученных показателей надежности заданным техническим требованиям системы. Допущения, принимаемые при логико-вероятностном методе: для элементов системы возможны только два состояния; метод применим для невосстанавливаемых систем; отказы элементов системы должны быть независимы. Пример решения задачи Имеется 2 автоматизированных рабочих места, между которыми есть 5 каналов связи, соединенных в виде мостиковой схемы. Определить вероятность безотказной работы каналов связи. Найти вероятность безотказной работы ИС, имеющей мостиковую структуру (рис. 2.4), если известны вероятности безотказной работы каждого элемента P1= P2=...= P5= 0,9. Решение ИС будет работоспособна, если в работоспособном состоянии находятся каналы: 1,2,3,4,5; 1,2,3,4; 1,5,4; 2,5,3; 1,3; 2,4. Составление логической функции работоспособности.  3. Приведение Fл к ортогональной бесповторной форме Fлo. Применяя формулу (5) вышеприведенных правил (см. 3-й этап методики расчета), получаем:  Приводим к бесповторному виду, раскладывая согласно формуле (9) правил преобразования, функцию FЛ: 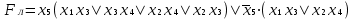 ; ;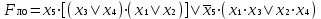 ; ;4. Арифметизация Fлo с целью нахождения Fа. Fa = x5[(x3 + x4 – x3x4)(x1 + x2 – x1x2)] + + (1 – x5)(x1x3 + x2x4 – x1x3x2x4). 5. Вычисляем вероятность безотказной работы. Поскольку вероятности безотказной работы каналов не зависят от времени и равны по величине 0,9, вероятность безотказной работы ИС Рс(t) определится как Pc = P5[(P3 + P4 – P3 P4)(P1 + P2 – P1 P2)] + + (1 – P5)(P1 P3 + P2 P4 – P1P2P3P4). Так как Pi= 0,9 для 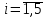 , то Pc = 0,978. , то Pc = 0,978. |