Основные понятия и определения теории надежности
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
СТАТИСТИЧЕСКАЯ ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ. Статистическая оценка показателей надежности при определительных испытаниях По результатам определительных испытаний могут быть получены: – точечная оценка показателей надежности; – определение законов распределения наработки на отказ; – интервальная оценка показателей надежности. При определительных испытаниях для высоконадежных систем можно наблюдать очень малое количество отказов или вообще их может не быть. Точечная оценка может «прыгать», тогда её не используют, а применяют интервальное оценивание. Фактический показатель надежности будет находиться внутри интервала между нижней и верхней границей с доверительной вероятностью 1-α: Вер {Тон < То < Тов} = 1-α Тон = То - Е1 Тов = То + Е2, где То – фактическое значение средней наработки на отказ; Е1, Е2 – погрешности в определении То. 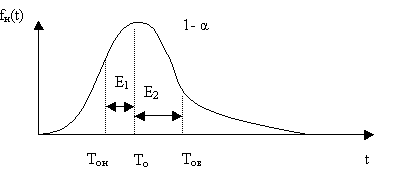 Рис. 3.1 Интервал допустимых значений наработки на отказ Рассмотрим формулу для расчета интегральных показателей в случае экспоненциального распределения наработки на отказ: 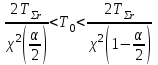 , ,где Т∑r – суммарная наработка на отказ в зависимости от плана, c2 – значение из таблицы c2 Пирсона, которое находится для числа степеней свободы К=2r и вероятностей α/2 и (1- α/2) 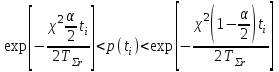 . .На практике, как правило, нужна только нижняя граница, тогда 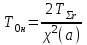 , , 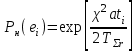 . .Показатель надежности не должен быть ниже нижней границы. СУЩНОСТЬ ТОЧЕЧНОГО И ИНТЕРВАЛЬНОГО ОЦЕНИВАНИЯ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ. Под оценками показателей надежности понимают точечную или интервальную (границы доверительного интервала, который с заданной вероятностью содержит истинное значение показателя) оценки показателя. Для вычисления оценок показателей надежности проводят следующие работы: 1) выбор плана испытаний на надежность; 2) планирование испытаний; 3) сбор необходимой информации; 4) статистическую обработку информации. По результатам определительных испытаний могут быть получены: – точечная оценка показателей надежности; – определение законов распределения наработки на отказ; – интервальная оценка показателей надежности. При определительных испытаниях для высоконадежных систем можно наблюдать очень малое количество отказов или вообще их может не быть. Точечная оценка может «прыгать», тогда её не используют, а применяют интервальное оценивание. Фактический показатель надежности будет находиться внутри интервала между нижней и верхней границей с доверительной вероятностью 1-α: Вер {Тон < То < Тов} = 1-α Тон = То - Е1 Тов = То + Е2, где То – фактическое значение средней наработки на отказ; Е1, Е2 – погрешности в определении То (рис. 3.1).         α 2 α 2  Рис. 3.1 Интервал допустимых значений наработки на отказ Рассмотрим формулу для расчета интегральных показателей в случае экспоненциального распределения наработки на отказ: 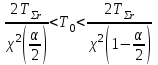 , ,где Т∑r – суммарная наработка на отказ в зависимости от плана, c2 – значение из таблицы c2 Пирсона, которое находится для числа степеней свободы К=2r и вероятностей α/2 и (1- α/2) 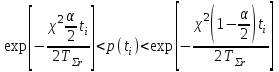 . .На практике, как правило, нужна только нижняя граница, тогда 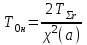 , , 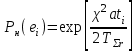 . .Показатель надежности не должен быть ниже нижней границы. Из интернета: Статистические определения показателей надежности являются их точечными оценками. Для определения показателей надежности проводятся наблюдения в процессе эксплуатации либо специальные испытания. Информация, полученная в результате этих наблюдении или испытаний, обрабатывается методами математической статистики. При испытаниях по плану NUN на испытания ставится N систем. Испытания ведутся до отказа всей системы. Время отказа t¡ фиксируется. В этом случае оценка средней наработки до отказа определяется следующим образом T= (20.1) Такие определение применим при любых законах распределения наработки до отказа. Для экспоненциального распределения при всех других рассмотренных выше планах испытании (кроме плана NUN) точечная оценка средней наработки до отказа определяется T= (20.2) где Ѕ – суммарная наработка всех систем за время испытаний, - суммарное число отказов всех систем за время испытаний. Например при плане NUТ S = + (N-m)T, (20.3) где m – число систем, отказавших в интервале (О,Т), t¡ - наработка до отказа i–й системы из числа отказавших (i = 1,m ). При плане испытаний NUR S = + (N-r)t, (20.4) где tr – время фиксации последнего отказа. Для плана NRТ и простейшего потока, у которого время между отказами подчиняются экспоненциальному распределению, оценка Т* ср осуществляется по формуле: T= = (20.5) Оценка интенсивности отказов λ* при экспоненциальном распределении может быть определена через оценку средней наработки до отказа: λ* = 1/ T (20.6) Например, при плане NUN λ* = N/ (20.7) Оценка параметра ω* простейшего потока совпадает с оценкой интенсивности отказов λ*. Например, при плане NRТ ω* = λ* = / NТ (20.8) При нормальном распределении, кроме оценки средней наработки до отказа, часто требуется найти точечную оценку и второго параметра этого распределения σ*, равного среднеквадратическому отклонению. Например, при плане NUN σ* = (20.9) где время отказа t фиксируется. Оценки вероятности отказа Q (t) до момента t : Q (t) = n(t)/ N, (20.10) где n(t) – число систем, отказавших к моменту t, могут быть найдены за ограниченный интервал времени t = Т и соответствует плану испытаний NUТ. Интервальные оценки Использование средних значении показателей надежности, получаемых путем точечной оценки позволяет решать задачи, возникающие в инженерной практике. Однако знание только среднего значения показателя надежности не всегда достаточно. Например, пусть n1 и n2 - соответственно число отказов, полученных при первом (испытывалось 10 изделий) испытаниях. Получены следующие результаты испытаний по плану NUN. t 100 200 300 400 500 600 700 800 n1 6 5 3 3 1 1 1 1 n2 1 2 4 2 1 - - - Средние значения наработки на отказ по результатам первого и второго испытаний одинаковы по приближенным формулам Т*ср1 = 6300/21 = 300час.; Т*ср2 = 3000/10 = 300 час. Но результаты первого испытания существенно отличаются от результатов второго испытания, прежде всего потому, что законы распределения времени до отказов нельзя считать одинаковыми (в первом он приближается к экспоненциальному, во втором – к нормальному). Количество испытуемых объектов на первом испытании более чем в два раза превышает количество объектов на втором испытании. Это вынуждает искать способы представить на основании результатов испытаний более информативные оценки по сравнению со средними. Одним из таких способов – способ оценки показателей надежности доверительным интервалом. Если испытывать всю партию, а не выборку из нее, то полученные характеристики называют генеральными. Обычно при испытаниях из генеральной совокупности выбираются n - образцов и испытываются. По результатам выборочных испытаний делается суждение (оценка) о надежности всей партии. При этом, естественно допускается некоторая ошибка Δx = / x – x /, где Δx – абсолютная ошибка среднего, x – выборочное среднее значение показателя надежности, x– генеральная средняя (истинное значение показателя надежности). Следовательно, истинное значение заключено в интервале: x – Δx < x < x + Δx, (20.11) где x ± Δx – называется доверительным интервалом, причем «+» соответствует верхней доверительной границе, а знак «-» нижней доверительной границе параметра x0. Однако, и такое утверждение не может считаться абсолютно достоверным, поскольку не указана надежность получаемого результата. Надежность результата оценивается так называемой доверительной вероятностью. Таким образом, доверительный интервал характеризует точность оценки, а доверительная вероятность – ее достоверность. Доверительная вероятность α- это вероятность того, что истинное значение оцениваемой величины попадает в найденный доверительный интервал, т.е.: α= Р [x – Δx < xо < x + Δx] (20.12) Величина доверительного интервала зависит от объема выборки и доверительной вероятности. Между доверительным интервалом и доверительной вероятностью так же существует определенная связь, которая зависит от закона распределения. Кроме доверительной вероятности, еще используется термин – уровень значимость β. Уровень значимость определяет вероятность того, что истинное значение выйдет из доверительной границы. Между α и β существует связь β = 1 - α. Значение доверительного интервала получают на основании информации о законе распределения времени до появления отказа (наработка до отказа). Числовые значения границ доверительного интервала зависят не только от заданной доверительной вероятности, но и от закона распределения случайной величины (например, времени до появления отказа). В некоторых литературах имеются специальные таблицы, позволяющие определять доверительные интервалы для различных законов распределения. В инженерной практике чаще всего приходится определять доверительные интервалы для: средней наработки на отказ по зафиксированным временам возникновения отказов; вероятности отказа по числу отказавших систем (изделий). Построение доверительного интервала покажем на примере. Испытание систем на безотказность, проведенные по плану NUN (где N = 10) показали следующие наработки до отказа
Требуется найти: точечную оценку среднего времени безотказной работы; определить доверительный интервал, соответствующий доверительной вероятности = 0,95. Полагаем, что среднее время безотказной работы распределена по нормальному закону. Среднее время безотказной работы: T= = 119 час. Среднеквадратическое отклонение: σ= = 17,2 час. Величину доверительного интервала можно определить используя распределения Стьюдента: Δx = t= 2,262*17,2/3,16 = 12 час. где t- функция распределения Стьюдента, определяется по специальной таблице, если известно и N. Следовательно: T- Δx < То < T+ Δx, где То – истинное значение. Если подставить числовые значение, получим 119 – 12 < То< 119+12 или 107< То< 131, т.е. среднее время безотказной работы лежат в пределах 117 ÷ 131 час с вероятностью 0,95. КОНТРОЛЬ НАДЕЖНОСТИ ИС. ОБЩИЕ ПОЛОЖЕНИЯ. При серийном производстве на предприятии возникает задача контроля надежности выпускаемых изделий. Контроль надежности может быть сплошным – каждое изделие подвергается испытанию на надежность. Но это очень дорогой способ. Выборочный контроль надежности – из всей партии выпускаемых изделий N берется выборка n изделий (n < N) и испытаниям подвергаются n изделий. Здесь возникают риски: – напрасной браковки всей партии N, которая содержит в основном надежные изделия, а в выборку n случайным образом попадают все ненадежные изделия - риск поставщика – ошибка первого рода a; – напрасной приемки всей партии N, которая содержит большое количество дефектных изделий, а в выборку n случайным образом попадает большинство надежные изделия – риск потребителя – ошибка второго рода b. Среди планов испытаний выборочного контроля выделяют: – планы типа однократной выборки, – планы типа двукратной выборки, – последовательный контроль надежности. В планах типа однократной выборки из общего количества N выпускаемых изделий выбирается n изделий и каждое подвергается контролю на надежность. Находится число дефектных изделий среди n изделий. Число дефектных изделий в выборке n – d(n). Приемочное число с – граничное число дефектных изделий определяется на базе оперативной характеристики. Если d(n) < c, то партия принимается, а если d(n) > c – партия бракуется. Если выполняется n ≥ 0,1,…,N, то можно принимать биноминальный закон распределения. Строится оперативная характеристика П(q), где 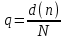 . .Биноминальный закон распределения: 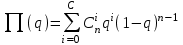 , ,где С – приёмочное число; Сni – число сочетаний из n по i. В планах типа двукратной выборки из общего числа изделий N выбирается n1 изделий (n1 > N). Эта выборка подвергается контролю на надежность и подсчитывается число дефектных изделий в n1. Если d(n1) ≤ c1, то партия принимается, d(n1) > c2 – партия бракуется. c1 < d(n1) ≤ c2 – зона неопределенности. Берется вторая выборка n2, такая, что (n1 + n2 < N) и подвергается контролю на надежность. Если d(n1 + n2) ≤ c3 – партия принимается, d(n1 + n2) > c3 – партия бракуется. Возможен вариант, когда c2 = c3. Оперативная характеристика П(q) = Ра1 + Ра2, где Ра1 и Ра2 –несовместимые события (рис. 3.3). Событие а1: d(n1) < c1; а2: d(n1 + n2) ≤ c2; d(n1) > c1 Партия изделий будет принята, если наступит одно из несовместных событий: – а1: для первой выборки выполняется условие 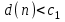 – а2: для двух последних выборок выполняются условия 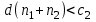 , , 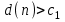 Тогда оперативная характеристика 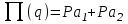 , ,где Ра1 – вероятность события а1, Ра2 – вероятность события а2. Ра1 вычисляется по формуле одновыборочного контроля, а Ра2 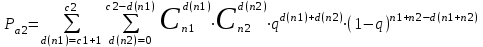 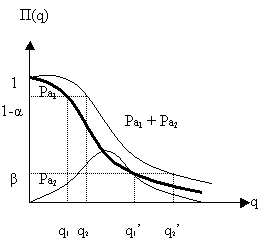 Рис. 3.3 Графическая иллюстрация плана двукратной выборки При последовательном контроле надежности берется целый ряд выборок и каждый раз сравнивается с приемочными числами. Необходимо, чтобы было соблюдено условие (n1 + n2+…+ni) ≤ N. Если d(n1 + n2+…+ni) = di. Тогда возмём выборку n1, подсчитаем d(n1) и сравним с передаточными числами. Если d1 ≤ c1 – партия принимается, d1 > c1’ – партия бракуется. c1 < d(n1) ≤ c1’ – зона неопределенности. Необходимо взять выборку n2 и подсчитать d2. Если d2 ≤ c2 – партия принимается, d2 > c2’ – партия бракуется. c1 < d(n1) < c2’ – зона неопределенности. Берём выборку n3 и так далее…Выборка ni. Если di < ci – партия принимается, di > cj’– партия бракуется; Последовательный контроль надежности проводится по накопленному числу дефектных изделий r = 1, 2, 3,… или по суммарной наработке на отказ Т∑r в зависимости от плана испытаний. В основе принятия решений лежит вероятность gr – отношение правдоподобия, r = 1,2,3,… которая и сравнивается с величинами риска поставщика и потребителя. Если 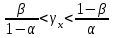 – продолжается испытание, 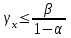 – партия принимается, 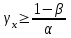 – партия бракуется. Рассмотрим практическую методику последовательного контроля надежности по суммарной наработке на отказ ТSr (рис. 3.4). 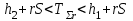 – испытание продолжается, – испытание продолжается,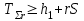 – партия принимается, 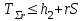 – партия бракуется. – партия бракуется. T∑r h1 + rS Продолжение испытаний Принимается h2 + rS Брак r            Рис. 3.4 Использование последовательного контроля надёжности 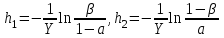 , ,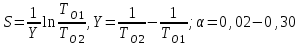 , ,Т01 – средняя наработка на отказ исправной системы по ее паспортным данным, Т02 – средняя наработка на отказ системы, которую считают надежной 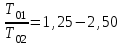 . . |
