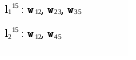Основные понятия и определения теории надежности

• Название: Основные понятия и определения теории надежности
• Дата: 12.04.2022
• Размер: 1.89 Mb.
• Имя файла: Nadezhnost_ispravlennaya.docx
• Тип: Документы; #467916
• страница: 2 из 8

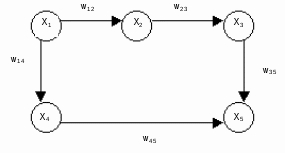
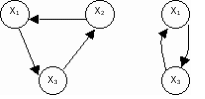
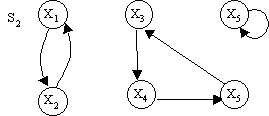
ТОПОЛОГИЧЕСКИЙ МЕТОД РАСЧЕТА НАДЕЖНОСТИ СИСТЕМ: ОСНОВНЫЕ ПОЛОЖЕНИЯ

Метод основан на использовании математического аппарата марковских процессов (вероятность нахождения системы в каком-либо состоянии в будущем не зависит от прошлых состояний системы).

Обозначим Х как множество состояний системы: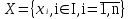
,
где xi – i-е состояние, I – множество индексов всех возможных состояний системы, n – количество возможных состояний системы.

Разобьем множество Х на два подмножества:

подмножество работоспособных состояний системы Хр;

подмножество неработоспособных состояний системы .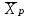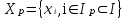
,

где Xр – подмножество работоспособных состояний системы, Iр – множество индексов работоспособных состояний системы.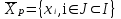
,

где 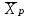– подмножество неработоспособных состояний системы, J – множество индексов неработоспособных состояний системы.

Нахождение системы в том или ином состоянии обусловливает случайный процесс X(t) перехода системы в пространстве ее состояний. X(t) называют также траекторией системы.

Представим X(t) в виде вероятностного графа состояний G(X, W), где Х – множество вершин графа, соответствующих множеству состояний X; W – множество дуг, соединяющих вершины данного графа; P1(t), ..., Pi(t), ..., P6(t) – вероятности нахождения системы в i-м состоянии; d(wij) – вес дуги wij; aij – интенсивность перехода из состояния i в состояние j (рис. 2.6).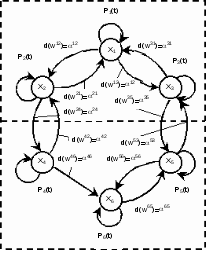



Рис. 2.6. Пример вероятностного графа состояний G(X,W)
Топологический метод использует аппарат теории графов применительно к решению задач надежности. Рассмотрим методику решения задач методом, который позволяет непосредственно по графу состояний G(X, W) без составления и решения уравнений Колмогорова вычислять показатели надежности. Для этого введем некоторые определения.

Прямой путь lij из вершины хi в вершину хj – цепь последовательно соединенных однонаправленных дуг, где каждая вершина имеет входящую и одну выходящую дуги, за исключением начальной и конечной, имеющих по одной дуге (рис. 2.7).

Рис. 2.7. Определение прямых путей на графе
Вес k-го прямого пути из вершины i в вершину j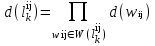
,

где 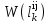- множество дуг, которые составляют k-ый прямой путь.

Замкнутый контур r – прямой путь, на котором начальная и конечная вершины совпадают (рис. 2.8). Вес замкнутого контура r
,
где 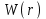– множество дуг, входящих в замкнутый контур r.



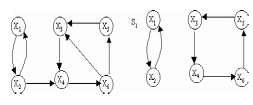
Рис. 2.8. Примеры замкнутых контуров


Частным случаем замкнутого контура является петля (рис. 2.9), в которой входящая и выходящие дуги сливаются в одну.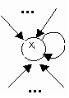



Рис. 2.9. Петля
Вес петли при вершине определяется как отрицательная сумма весов дуг, исходящих из этой петли: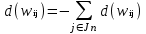


где Jn – множество индексов вершин, которые связаны с i-ой вершиной выходящими из нее дугами.

Соединение графа S – это частичный граф, который образуют только замкнутые контуры. Частичный граф представляет собой все вершины, некоторые дуги и петли исходного графа, которые составляют независимые замкнутые контуры (то есть контуры, не имеющие общих вершин). Один граф может располагать несколькими соединениями (рис. 2.10). При образовании соединений следует помнить, что каждая вершина графа G (X, W) имеет петлю.

Рис. 2.10. Пример образования соединения графа

Вес j-го соединения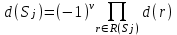
,

где  – число независимых замкнутых контуров, образующих соединение, R(Sj) – множество независимых замкнутых контуров, образующих соединение.

Определитель графа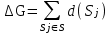
,
где S — множество всех возможных соединений графа.

7. 
   ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ПРИ ТОПОЛОГИЧЕСКОМ МЕТОДЕ РАСЧЕТА.
   

Теперь рассмотрим методику расчета показателей надежности топологическим методом в установившемся режиме, где топологические коэффициенты Сi для каждой xi вершины графа определяются непосредственно по графу, а затем вычисляется нужный показатель по ниже приведенным топологическим формулам.

Для определения коэффициента Сi необходимо:

– выбрать начальную вершину графа xq отдельно для определения каждого из коэффициентов Сi ( 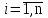); начальная вершина может быть выбрана произвольно, однако выбор влияет на объем вычислений, поэтому ее надо выбирать так, чтобы были длинные прямые пути;

– построить множество К прямых путей из начальной вершины xq в вершину xi, для которой определяется коэффициент;

– для каждого k-го прямого пути построить множество замкнутых контуров подграфа G{Xk} и образовать возможные комбинации независимых замкнутых контуров (множество соединений S), где G{Xk} – подграф графа G{X, W}, образованный удалением множества вершин, входящих в k-й путь и прилегающих к нему дуг;

– записать коэффициенты Ci по найденным составляющим по формуле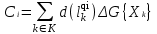

гдe К – множество прямых путей из произвольно выбранной вершины хq в хi; Хк - множество вершин, входящих в k-ый прямой путь.

Используя топологические коэффициенты, основные показатели надежности установившегося режима можно записать:

– вероятность нахождения системы в i-м состоянии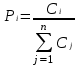

,

где n – число вершин графа;

– коэффициент готовности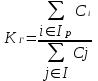

,

где Ip – множество индексов работоспособных состояний системы;

– коэффициент простоя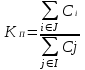

,

где J – множество индексов неработоспособных состояний системы;

– среднюю наработку на отказ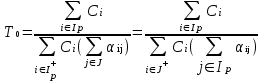

,

где 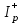– подмножество индексов граничных состояний из Xр, из которых в неработоспособное состояние можно попасть за один переход;

– среднее время восстановления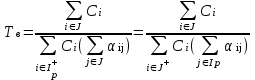

,

где J+ – подмножество индексов граничных состояний из 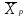, из которых в работоспособное состояние можно попасть за один переход.

Основные положения топологического метода могут быть применены для определения показателей надежности неустановившегося режима с использованием преобразований Лапласа.
Пример решения задачи

Имеется ИС, которая состоит из 2-х серверов. При работоспособности одного из серверов система работоспособна, так как каждый сервер может выполнять все функции.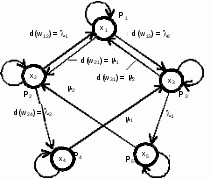







Рис. 2.11. Вероятностный граф состояний

Для обслуживания серверов существует одна бригада, ремонтирующая одновременно только один сервер, который отказал первым.

Необходимо определить топологическим методом показатели надежности.
Решение

Работоспособные состояния: x1 – оба сервера в работоспособном состоянии; x2 – отказ 1-го сервера и его восстановление, 2-й в работоспособном состоянии; x3 – отказ 2-го сервера и его восстановление, 1-й в работоспособном состоянии.

Неработоспособные состояния: x4 – при восстанавливающемся 1‑м сервере, отказал и 2-й; x5 – при восстанавливающемся 2-м сервере, отказал 1-й сервер (рис. 2.11).

Вычисляем топологические коэффициенты. Для нахождения коэффициента C1 в качестве начальной выбираем вершину x5.
С1=52244331 + 5221(-1)=2d(w33)d(w44) = 5221[-(35+31)]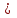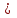

(-43) + 52244331 = m2m12(1+m2) + m222m1 =

= m2m1(m11 + m1m2 +m22).
Для нахождения коэффициента C2 в качестве начальной выбираем вершину x4.

С2=433552(-1)=1d(w11) + 433112(-1)=1d(w55) =

m11m2(1 + 2 ) + m1m221 = m1m2(21+ 12+ 1 m2),
С3= m1m2(22+ 12+ 2 m1),
С4= 12m2(1+ m2 + 2),
С5= 12m1(2+ m1 + 1).
Теперь можно определить искомые показатели надежности.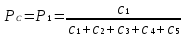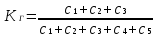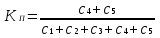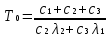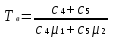
,
,
,
,
.

8. 
   РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ НА ОСНОВЕ СИСТЕМЫ УРАВНЕНИЙ КОЛМОГОРОВА.
   

Для расчета характеристик надежности восстанавливаемых систем вычислительной техники пользуются формулами, полученными на основе использования непрерывных Марковских цепей дискретных систем и дифференциальных уравнений А.Н. Колмогорова.

Для исследования Марковских цепей рассматривают возможные состояния системы и изменения состояний с помощью графов состояний. Восстанавливаемая система в общем случае имеет три состояния: G — исправное, G — неисправное, но работоспособное, G — неработоспособное (рис. 4).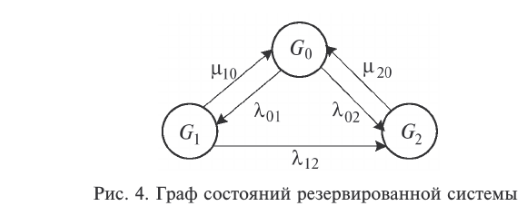

Переход системы из состояния в состояние происходит под воздействием потоков отказов и восстановлений. Если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими (*ординарный поток однородных событий, для которого число событий в интервале А не зависит от чисел событий в любых интервалах, не пересекающихся с А, и подчиняется распределению Пуассона), то случайный процесс есть марковский процесс и задается системой дифференциальных уравнений.

Вывод дифференциальных уравнений выполнен из рассмотрения смены состояний системы. Пусть система в момент времени t находится в состоянии G . Рассмотрим элементарный промежуток времени, примыкающий к моменту времени t. Назовем плотностью вероятности перехода из состояния G в состояние G (или интенсивностью перехода) предел отношения вероятности перехода p (∆t) к длине промежутка ∆t. Запись этого отношения имеет вид

9. 
   МЕТОДЫ ПОВЫШЕНИЯ (ОБЕСПЕЧЕНИЯ) НАДЕЖНОСТИ
   

Все системы подразделяются на восстанавливаемые и невосстанавливаемые. Невосстанавливаемые системы эксплуатируются до первого отказа. У восстанавливаемых систем может быть поток отказов. Кроме того, системы делятся на ремонтируемые и неремонтируемые. Это технические термины, говорящие о возможности ремонта системы. Так как ремонт может быть дорогой или в условиях эксплуатации не возможным, то система может быть ремонтируемой, но относится к классу невосстанавливаемых.

Понятия восстанавливаемых и невосстанавливаемых систем применяются для расчетов их надежности.

В связи с различными этапами жизненного цикла возникают специфические задачи обеспечения надежности ИС и используются соответствующие методы оценки надежности:

1. 
   Этап проектирования. Схемно-конструктивные методы повышения надежности:
   

• 
  Выбор и обоснование показателя эффективности ИС и определение его взаимосвязи с показателем надежности;
  
• 
  Нормирование надежности. Определение оптимального уровня показателя надежности системы, которой она должна обладать во время эксплуатации системы;
  
• 
  Расчет показателя надежности всей системы, если известны показатели надежности всех элементов;
  
• 
  Решение задачи оптимального резервирования (дублирования отдельных элементов).
  

2. 
   Этап изготовления. Производственные методы повышения надежности:
   

• 
  Автоматизация технологических процессов;
  
• 
  Методы статистического регулирования надежности;
  
• 
  Тренировка элементов и систем (испытание сложной системы в течение небольшого промежутка времени с тем, чтобы выявить производственные дефекты).
  

3. 
   Этап эксплуатации. Эксплуатационные методы повышения надежности:
   
   • 
     Использование диагностических систем, которые выявляют скрытые дефекты;
     
   • 
     Прогнозирование отказов системы.
     

Применение гибкой системы технического обслуживания и ремонта (ремонт производится в зависимости от состояния системы).

10. 
    РЕЗЕРВИРОВАНИЕ. ВИДЫ И МЕТОДЫ РЕЗЕРВИРОВАНИЯ.
    

Резервирование - способ повышения надежности системы путем включения в состав системы резерва предусмотренного на стадии проектирования этой системы или во время эксплуатации. Представлена несколькими методами и видами резервирования и возможными их комбинациями.

Ниже показана схема возможных методов и видов резервирования и возможных их комбинаций: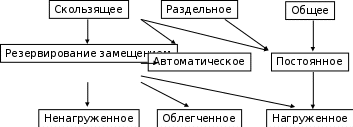



Рис. 4.1. Методы и виды резервирования.

Резервирование замещением: при отказе элемента система перестраивается и в замен отказавшего подключается элемент из числа резервных.

Автоматическое: при отказе основного элемента автоматически подключается резервный.

Постоянное: резервные и основные элементы находятся в одинаковых условиях и параллельно выполняют заданные функции.

Общее: резервируется вся система в целом.

Раздельное: резервируются отдельные участки системы.

Скользящее: один резервный элемент предназначен для резервирования некоторого множества основных элементов такого же типа. При отказе он заменяется.

Нагруженное: резервные элементы системы находятся во включенном состоянии, работают параллельно с основными элементами и практически одинаково расходуют свой ресурс работы.

Ненагруженное: резервные элементы находятся в выключенном состоянии и практически не расходуют свой ресурс работы.

Облегченное: резервные элементы находятся во включенном состоянии однако расходуют свой ресурс намного меньше чем при подключении их на место основных.

11. 
    ОСНОВНЫЕ ПОНЯТИЯ, ПРИМЕНЯЕМЫЕ ПРИ СТРУКТУРНОМ МЕТОДЕ РАСЧЕТА НАДЕЖНОСТИ СИСТЕМ.
    

В основе метода лежит формализация деятельности человека-оператора в процессе решения в виде последовательной структуры. Структура – специальная логическая цепь, отображающая процесс функционирования системы человек-техника с количественными характеристиками единиц деятельности. Каждое звено имеет свои показатели надежности, которые потом используются в расчете надежности всей системы.

Деятельность человека последовательно представляется состоящей из 1) операционных, 2) функциональных и 3) программных единиц.

Низший уровень рассмотрения деятельности человека-оператора – уровень операционных единиц.

Операционная единица – отдельный психофизиологический акт – является наименьшей единицей, до которой расчленяется деятельность человека-оператора, например, поворот ключа, нажатие кнопки и т. д.

Функциональная единица – группа операционных единиц, объединенных в структуре деятельности человека, в технологическом или смысловом отношении. Это специальные функциональные операции (блоки операций), подразделяемые на основные и вспомогательные функциональные единицы.

Основные единицы – единицы (блоки), в результате деятельности которых происходит достижение цели. К ним относят рабочий блок, блок задержки, блок принятия решений.

Вспомогательные блоки вводятся в структуру деятельности для увеличения безошибочности выполнения операций. При идеальной работе человека-оператора они не нужны (блок контроля ошибок, блок диагностического контроля).

Программная единица – совокупность функциональных единиц, объединенных в законченные блоки (программы), например, пуск насоса, подача топлива и т. д.