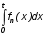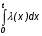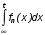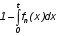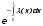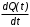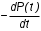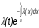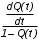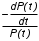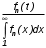Основные понятия и определения теории надежности
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
СХЕМЫ ОДНОКРАТНОЙ И ДВУКРАТНОЙ ВЫБОРКИ ПРИ КОНТРОЛЕ Среди планов испытаний выборочного контроля выделяют: – планы типа однократной выборки, – планы типа двукратной выборки, – последовательный контроль надежности. В планах типа однократной выборки из общего количества N выпускаемых изделий выбирается n изделий и каждое подвергается контролю на надежность. Находится число дефектных изделий среди n изделий. Число дефектных изделий в выборке n – d(n). Приемочное число с – граничное число дефектных изделий определяется на базе оперативной характеристики. Если d(n) < c, то партия принимается, а если d(n) > c – партия бракуется. Если выполняется n ≥ 0,1,…,N, то можно принимать биноминальный закон распределения. Строится оперативная характеристика П(q), где 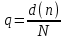 . .Биноминальный закон распределения: 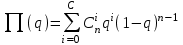 , ,где С – приёмочное число; Сni – число сочетаний из n по i. В планах типа двукратной выборки из общего числа изделий N выбирается n1 изделий (n1 > N). Эта выборка подвергается контролю на надежность и подсчитывается число дефектных изделий в n1. Если d(n1) ≤ c1, то партия принимается, d(n1) > c2 – партия бракуется. c1 < d(n1) ≤ c2 – зона неопределенности. Берется вторая выборка n2, такая, что (n1 + n2 < N) и подвергается контролю на надежность. Если d(n1 + n2) ≤ c3 – партия принимается, d(n1 + n2) > c3 – партия бракуется. Возможен вариант, когда c2 = c3. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА ПРОВЕДЕНИЯ КОНТРОЛЯ При последовательном контроле надежности берется целый ряд выборок и каждый раз сравнивается с приемочными числами. Необходимо, чтобы было соблюдено условие (n1 + n2+…+ni) ≤ N. Если d(n1 + n2+…+ni) = di. Тогда возьмём выборку n1, подсчитаем d(n1) и сравним с передаточными числами. Если d1 ≤ c1 – партия принимается, d1 > c1’ – партия бракуется. c1 < d(n1) ≤ c1’ – зона неопределенности. Необходимо взять выборку n2 и подсчитать d2. Если d2 ≤ c2 – партия принимается, d2 > c2’ – партия бракуется. c1 < d(n1) < c2’ – зона неопределенности. Берём выборку n3 и так далее…Выборка ni. Если di < ci – партия принимается, di > cj’– партия бракуется; Последовательный контроль надежности проводится по накопленному числу дефектных изделий r = 1, 2, 3,… или по суммарной наработке на отказ Т∑r в зависимости от плана испытаний. В основе принятия решений лежит вероятность gr – отношение правдоподобия, r = 1,2,3,… которая и сравнивается с величинами риска поставщика и потребителя. Если 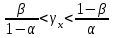 – продолжается испытание, 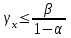 – партия принимается, 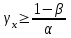 – партия бракуется. Рассмотрим практическую методику последовательного контроля надежности по суммарной наработке на отказ ТSr (рис. 3.4). 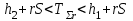 – испытание продолжается, – испытание продолжается,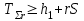 – партия принимается, 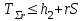 – партия бракуется. – партия бракуется. T∑r h1 + rS Продолжение испытаний Принимается h2 + rS Брак r 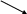           Рис. 3.4 Использование последовательного контроля надёжности 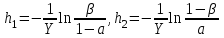 , ,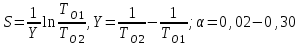 , ,Т01 – средняя наработка на отказ исправной системы по ее паспортным данным, Т02 – средняя наработка на отказ системы, которую считают надежной 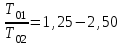 . .ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ. Невосстанавливаемыми называются такие объекты, для которых восстановление работоспособного состояния не предусмотрено в нормативно-технической и (или) конструкторской (проектной) документации [7]. Если происходит отказ такого изделия, то выполняемая операция будет сорвана, и ее необходимо начинать вновь в том случае, если возможно устранение отказа. К таким изделиям относятся как изделия однократного действия (ракеты, управляемые снаряды, искусственные спутники Земли, усилители системы подводной межконтинентальной связи и т. п.), так и изделия многократного действия (некоторые системы навигационного комплекса судового оборудования, системы ПВО, системы управления воздушным движением, системы управления химическими, металлургическими и другими ответственными производственными процессами и т. д.). Для невосстанавливаемых объектов применяется понятие наработка до отказа (он же является и последним отказом). В расчетах пользуются средней наработкой до отказа, определяемой в [7] как математическое ожидание наработки объекта до первого отказа. Средняя наработка до отказа Т1 вычисляется по формуле 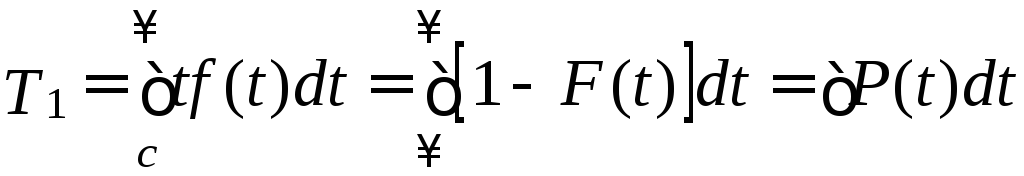 , (3.7) , (3.7)где F(t) – функция распределения наработки до отказа; Р(t) – вероятность безотказной работы; f(t) – плотность распределения наработки до отказа. Статистически средняя наработка до отказа определяется по формуле 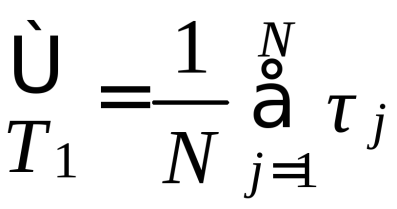 , (3.8) , (3.8)где N – число работоспособных объектов при t = 0; – наработка до первого отказа каждого из объектов. Для дифференцируемых функций распределения случайной величины определяется первая производная, называемая плотностью распределения (законом распределения) времени работы объекта до отказа: 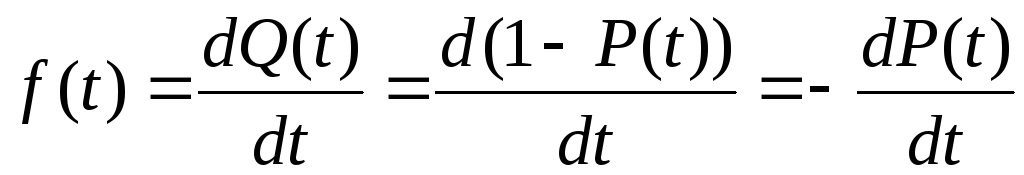 . (3.9) Другим важным показателем надежности является интенсивность отказов, которая сообщает, какая часть объектов выходит из строя в единицу времени относительно среднего числа исправно работающих объектов. Интенсивность отказов как статистический параметр – отношение числа отказавших объектов в единицу времени к числу объектов, продолжающих безотказно работать в данный промежуток времени: 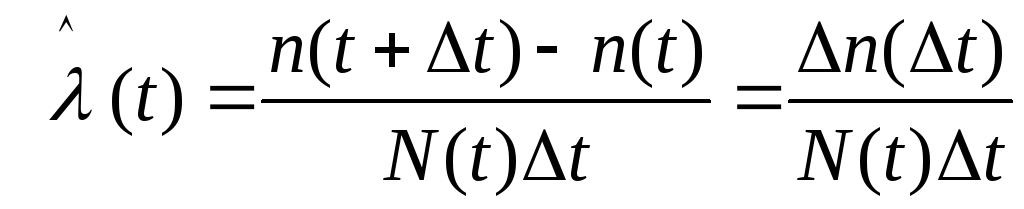 , (3.10) , (3.10)где Δn(Δt) – число отказавших объектов за промежуток времени от (t – Δt / 2) до (t + Δt / 2), 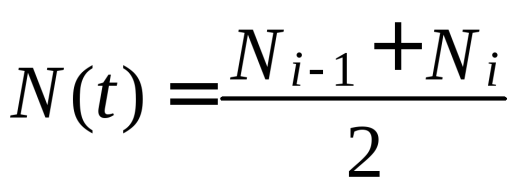 , (3.11) , (3.11)где Ni – 1 – число исправно работающих объектов в начале интервала Δt; Ni – число исправно работающих объектов в конце интервала Δt. Интенсивность отказов как вероятностный параметр – условная плотность вероятности возникновения отказа изделия при условии, что до рассматриваемого момента времени t отказ не возник [7]: где функции f(t) и λ(t) измеряются в часах в минус первой степени. При интегрировании (3.12) получается: 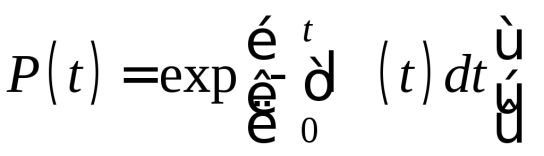 . (3.13) . (3.13)Величина λ(t)dt есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t], откажет в интервале [t, t + dt]. Выражение (3.12), называемое основным законом надежности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени. +В частном случае постоянства интенсивности отказов λ(t) == const выражение (3.12) преобразуется в известное в теории вероятностей экспоненциальное распределение 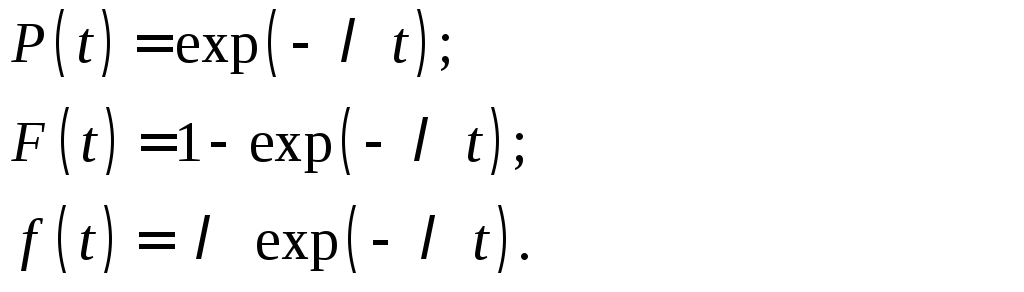 Таким образом, для невосстанавливаемых объектов применяют показатели Р(t), Т1, f(t), λ(t). МЕТОДЫ И ВИДЫ РЕЗЕРВИРОВАНИЯ. Резервирование - способ повышения надежности системы путем включения в состав системы резерва предусмотренного на стадии проектирования этой системы или во время эксплуатации. Представлена несколькими методами и видами резервирования и возможными их комбинациями. Ниже показана схема возможных методов и видов резервирования и возможных их комбинаций:  Рис. 4.1. Методы и виды резервирования. Резервирование замещением: при отказе элемента система перестраивается и в замен отказавшего подключается элемент из числа резервных. Автоматическое: при отказе основного элемента автоматически подключается резервный. Постоянное: резервные и основные элементы находятся в одинаковых условиях и параллельно выполняют заданные функции. Общее: резервируется вся система в целом. Раздельное: резервируются отдельные участки системы. Скользящее: один резервный элемент предназначен для резервирования некоторого множества основных элементов такого же типа. При отказе он заменяется. Нагруженное: резервные элементы системы находятся во включенном состоянии, работают параллельно с основными элементами и практически одинаково расходуют свой ресурс работы. Ненагруженное: резервные элементы находятся в выключенном состоянии и практически не расходуют свой ресурс работы. Облегченное: резервные элементы находятся во включенном состоянии однако расходуют свой ресурс намного меньше чем при подключении их на место основных. КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ БЕЗОПАСНОСТИ. Рассмотрим количественные показатели случайных величин, которые могут характеризовать свойства безотказности, ремонтопригодности, сохраняемости и долговечности. В качестве единиц измерения применяются: - для безотказности - непрерывное время безотказной работы системы (наработка на отказ T’); - для долговечности - время от момента изготовления системы до предельного состояния или списания. (срок службы T’’); - для ремонтнопригодности - время восстановления работоспособности T’’’; - для сохраняемости - случайное время сохранения работоспособности в состоянии хранения “T”. Показатели безотказности невосстанавливаемых систем В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t) , которая в данном случае будет называться функцией вероятности отказа Q ( t ), т.е.: 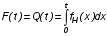 . .Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t: 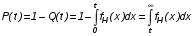 . .Графики, дающие представление о характерах изменения функций P(t) и Q(t), представлены на рисунке: 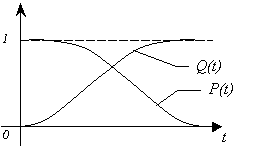 Рис.1.6. График изменения функций P(t) и Q(t) Плотность распределения вероятностей как показатель безотказности невосстанавливаемых систем принимает смысл плотности распределения наработки на отказ fH(t), а интенсивность (t) принимает смысл функции интенсивности отказов l(t): 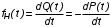 . . 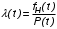 . . Между функциями P(t) и l(t) существует взаимосвязь: 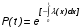 . . Взаимосвязь между функциями fH(t) и l(t) можно определить из соотношения: 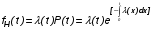 . .Если одна из четырех функций известна, то остальные три можно вычислить по формулам, приведенным в таблице. Удобный и наглядный физический смысл имеет показатель "средняя наработка на отказ", который равен математическому ожиданию времени исправной работы до первого отказа: 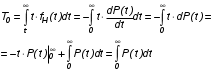 . .Свойства функции безотказной работы P(t): 1.При t=0, P(t)=1 , т.е. в нулевой момент времени система будет работоспособна. 2. P(t) — монотонно убывающая функция во времени. 3.При t→∞, P(t) → 0.
На практике часто требуется определить показатели безотказности при том условии, что элемент, проработавший время t1, будет безотказно работать в течение промежутка времени от t1 до t2 (t2>t1). В этом случае основные показатели находятся как условные вероятности. Условная вероятность безотказной работы в течение наработки t = t2 - t1 (рис. 1.7) при условии, что система безотказно проработала от 0 до t1, равна: 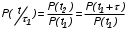 . .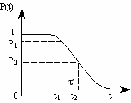 Рис.1.7. График условной вероятности работы системы Условная вероятность отказа равна: 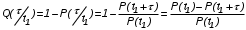 . . Условная интенсивность отказа равна: 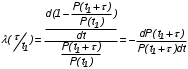 . . Условная наработка на отказ равна: 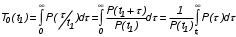 . . Теперь перейдем к рассмотрению статистических оценок показателей безотказности, которые в литературе обозначаются либо символом ^ либо *. Пусть на испытания было поставлено No систем, которые с течением времени отказывали, что модно представить временной диаграммой (No - количество изделий, n(t) - количество отказавших изделий за время t): 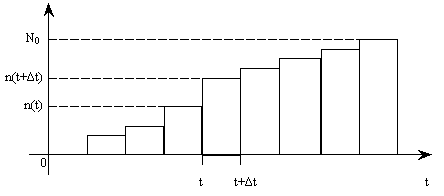 Рис.1.9. Результаты испытания No систем Показатели безотказности можно оценивать приближенно по статистическим данным. Рассмотрим формулы для определения статистических значений показателей безотказности. Статистическая оценка вероятности отказа: 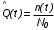 . .Статистическая оценка вероятности безотказной работы: 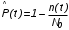 . .Статистическая оценка плотности распределения наработки на отказ: 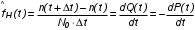 . .Статистическая оценка интенсивности отказов:  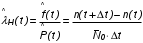 , ,где 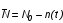 . .Статистическая оценка средней наработки на отказ находится по формуле: 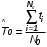 , , где ti — наработка на отказ i-й системы. Показатели безотказности восстанавливаемых систем Восстанавливаемые системы имеют поток отказов и периодически подвергаются воздействию системы технического обслуживания и ремонта. (рис.1.9), где  Рис.1.9. Процесс эксплуатации ti — i-ая наработка на отказ. ti — i-ое время восстановления после i-ого отказа Случайную величину длительности безотказной работы между соседними периодами восстановления системы можно характеризовать функцией распределения длительности безотказной работы между окончанием восстановления после (i-1)-го отказа и моментом наступления i-го отказа Fi(t). Тогда показатель Qi(t) = Fi(t) будет означать вероятность наступления отказа системы за промежуток времени t после окончания (i-1)-го восстановления. Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t: 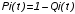 . .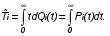 . .Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа: Toi Перечисленные показатели можно назвать локальными. Они характеризуют безотказность в интервалах времени между двумя соседними отказами. Частным случаем локальных показателей безотказности восстанавливаемых систем будут показатели безотказности невосстанавливаемых систем, если рассматривать свойства безотказности до первого отказа 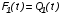 ; ; 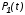 ; ; 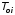 и т.д. и т.д. Для общего случая, который учитывает все отказы за интервал времени t, используются общие показатели безотказности, в частности ведущая функция потока отказов W(t) (математическое ожидание случайного числа отказов за время t): 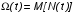 , ,где М – математическое ожидание; N(t) – случайное число отказов. Следующий общий показатель безотказности - параметр потока отказов (среднее значение количества отказов в единицу времени за рассматриваемый интервал времени - имеет вид 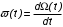 . .Справедливо обратное соотношение 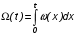 . .Наглядной характеристикой восстанавливаемых систем является среднее значение параметра потока отказов за рассматриваемую наработку TP: 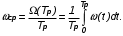 Среднюю наработку между отказами восстанавливаемого изделия характеризует показатель Т: 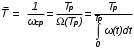 . .Предел параметра потока отказов 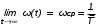 . .Показатель (t) связан с показателями невосстанавливаемых изделий f(t) и (t) неравенством 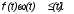 . .Если случайные величины наработки между отказами одинаково распределены и независимы (одинаковые законы распределения случайной величины наработки между отказами), т.е. F1(t) = F2(t) = … = Fk(t), то (t) связан с плотностью распределения наработки между отказами f(t) уравнением возобновления 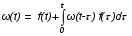 . .В некоторых случаях удобно искать решение преобразование Лапласа: 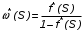 , ,где 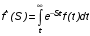 . .Если функция распределения наработки между отказами подчиняется экспоненциальному закону распределения, то расчет значительно упрощается. | |||||||||||||||||||||||||||||

 (t)
(t)