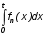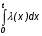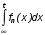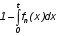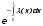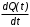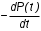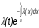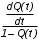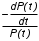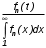Основные понятия и определения теории надежности
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
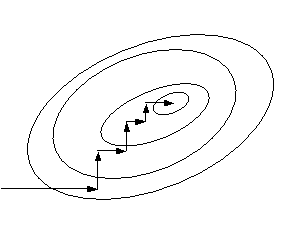
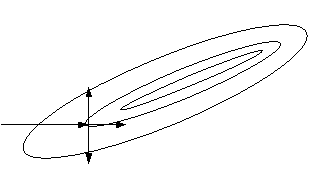
Показатели сохраняемости Определение свойств сохраняемости аналогично определению свойств безотказности с тем лишь различием, что они относятся к разным условиям: свойство безотказности характеризует рабочие эксплуатационные условия, а свойство сохраняемости – нерабочие условия (хранение и транспортировка). Показатели сохраняемости аналогичны показателям безотказности. Однако вычислять их нужно не через функции fн(t) и Q(t), а через законы распределения длительности безотказного хранения fхр(t) и Fхр(t). Срок сохраняемости – календарная продолжительность хранения или транспортировки изделия, в течение и после которой сохраняются значения показателей безотказности, долговечности и ремонтопригодности в установленных пределах. Из всего множества показателей сохраняемости наиболее часто в технической документации используют только два: средний срок сохраняемости и гамма-процентный срок сохраняемости. Средний срок сохраняемости — математическое ожидание случайной величины хранения до отказа: 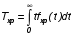 . .Гамма-процентный срок сохраняемости — срок сохраняемости, который достигается объектом с вероятностью g выраженной в процентах Tхр.: 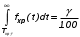 . .Рекомендуются значения = 90; 95 и 98%. Кроме того, применяют еще и медианный срок сохраняемости при = 50% Tхрμ: 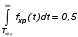 . .Показатели ремонтопригодности Свойство ремонтопригодности в принципе можно определять, как и все остальные свойства надежности, через соответствующие показатели, которые определяются через законы распределения длительности восстановления fв(t) и Fв(t). Из всей номенклатуры предлагаемых показателей для характеристики свойства ремонтопригодности применяют следующие: -интенсивность восстановления 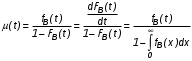 . .-среднее время восстановления 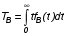 . .-и вероятность восстановления за заданное время 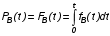 . .Показатели долговечности В качестве случайных величин, характеризующих долговечность технических систем, применяют две: -ресурс - наработка системы до списания выраженная во временных единицах измерения без учета простоев; -срок службы - календарная продолжительность службы объекта до его списания. Считаются известными законы распределения случайной величины ресурса fр(t) и Fр(t) или случайной величины срок службы fсл(t) и Fсл(t). Рассмотрим наиболее употребимые показатели долговечности. 1) Средний ресурс или средний срок службы – математическое ожидание средней величины ресурса или срока службы совокупности изделий одного типа и исполнения: 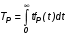 , ,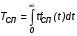 . .2) Гамма-процентный ресурс или срок службы, который имеют и превышают в среднем определенное число - процентов изделий Tрg, Tслg: 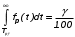 , ,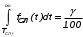 . .3) Медианный ресурс или срок службы Трм, Тслм: 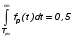 , ,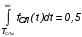 . .НАДЕЖНОСТЬ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ИС. ФАКТОРЫ, ВЛИЯЮЩИЕ НА НАДЕЖНОСТЬ ПО ИС. Надежность программного обеспечения - способность программного продукта безотказно выполнять определенные функции при заданных условиях в течение заданного периода времени с достаточно большой вероятностью. Степень надежности характеризуется вероятностью работы программного продукта без отказа в течение определенного периода времени. Существует 4 основные составляющие функциональной надежности программных систем (по его методичке: безотказность, долговечность, ремонтопригодность, сохраняемость): безотказность - свойство программы выполнять свои функции вовремя эксплуатации; работоспособность - свойство программы корректно (так как ожидает пользователь) работать весь заданный период эксплуатации; безопасность - свойство программы быть не опасной для людей и окружающих систем; защищенность - свойство программы противостоять случайным или умышленным вторжениям в нее. К числу основных факторов, влияющих на надежность ПО отнесены: взаимодействие ПО с внешней средой (программно-аппаратная средства, трансляторы, ОС). Этот фактор вносит наименьший вклад в надежность ПО при современном уровне надежности аппаратуры, ОС и компиляторов; взаимодействие с человеком (разработчиком и пользователем); - организация ПО (проектирование, постановка задачи и способы их достижения и реализации) и качество его разработки. Этот фактор вносит наибольший вклад в надежность; тестирование. ОСОБЕННОСТИ ОБЕСПЕЧЕНИЯ НАДЕЖНОСТИ ПРОГРАММНЫХ СРЕДСТВ ЭИС. Из интернета: Информационная система — это сложная человеко-машинная система, включающая в свой состав эргономические звенья, технические средства и программное обеспечение. Все методы обеспечения надежности и достоверности ИС можно отнести к двум классам. Один включает в себя методы, обеспечивающие безошибочность (безотказность, бессбойность) функциональных технических, эргономических и программных звеньев ИС, то есть, в конечном счете, повышающие их надежность. Другой — методы, обеспечивающие обнаружение и исправление ошибок, возникающих в информации, то есть методы контроля достоверности информации и ее коррекции, косвенно также повышающие функциональную надежность системы. Виды обеспечения надежности: экономическое; временное; организационное; структурное; технологическое; эксплуатационное; социальное; эргономическое; алгоритмическое; синтаксическое; семантическое. Обеспечение можно определить как совокупность факторов (элементов, методов, приемов, процедур, ресурсов и т. п.), способствующих достижению поставленной цели. Экономическое и временное обеспечения, обусловливаемые необходимостью соответственно материальных и временных затрат, используются для реализации процедур обеспечения достоверности. Организационное, эксплуатационное, техническое, социальное и эргономическое обеспечения применяются преимущественно для повышения надежности систем, а структурное и алгоритмическое обеспечения - для обоих классов методов. Пути повышения надежности эргономической составляющей. Для повышения надежности эргономической составляющей ЭИС используются методы контроля функционирования систем, обучение операторов, введение избыточности. Основная цель контроля функционирования любой ЭИС состоит в умении оценивать текущие ее состояния (операторов, в частности) и осуществлять проверку их соответствия требуемому качеству функционирования системы путем составления суждения и принятия решения по управлению состояниями ЭИС в целях обеспечения требуемого качества ее функционирования. Информационная модель контроля состоянии ЭИС определяется двумя основными принципами: • управленческим (структурным) согласованием информационных потоков; • информационным (функциональным) согласованием информационной среды в эргономическом контуре управления системой. Информационные потоки в ЭИС организуются таким образом, чтобы удовлетворять специфике и ограниченным возможностям организма оператора. Необходима адаптация деятельности оператора к особенностям технических средств. Задача контроля состоит в формировании входных характеристик ЭИС, определении выходных параметров (результатов функционирования ЭИС) и оценке ее состояний (или состояний параметров) по некоторому критерию в целях сравнения текущих состояний с допустимыми. При выполнении рабочих заданий человек-оператор может допускать ошибки, которые формируют тот или иной уровень надежности (либо качество) функционирования системы, причем контроль осуществляется путем организации контуров обратной связи. Различаются внутренние контуры обратной связи, т.е. контуры контроля и управления состояниями операторов, внешние контуры обратной связи, включающие в себя контуры результатов функционирования всей системы и контуры адаптации с внешней средой (социальной или экологической). Если сформировать критерий контроля состояний в виде наглядного образа – эрготического портрета (психофизического состояния) оператора, затем этот критерий вывести во внутренний контур обратной связи (контур контроля и управления состояниями операторов), то появляется возможность контролировать и управлять состояниями операторов ЭИС в диалоговом режиме, что позволяет резко повысить надежность и качество ее функционирования. Опыт эксплуатации автоматизированных систем показывает, что около трети всех отказов системы происходит вследствие недостаточной подготовленности обслуживающего персонала. В ряде случаев снижение надежности системы за счет этого фактора бывает настолько велико, что практически сводит к нулю высокий исходный коэффициент ее надежности. Несмотря на специальную подготовку оператор иногда допускает ошибки, применяя непригодный в данный момент алгоритм действий. Причины таких ошибок многообразны, но специальный психологический анализ показывает, что многие из них являются следствием недостатков организации обучения и отсутствия достаточно обоснованных критериев необходимой степени обученности. Из интернета (Леонтьев «Информатика»): Надежность ЭИС определяется не только отказами технических средств, но и отказами программного обеспечения (ПО), вызываемыми ошибками в программах [19]. Если отказы КТС зависят от времени и не зависят от обрабатываемой информации, то отказы ПО, наоборот, не зависят от времени, зато зависят от обрабатываемой входной информации, а также от текущего состояния системы. Оценка надежности ПО может быть получена непосредственно на основе свойств программ. В качестве исходных предпосылок принимаются следующие: а) в результате выполнения программы для каждого множества входных данных получается однозначный выходной результат; б) множество всех входных данных определяет все вычисления, выполняемые программой; в) каждая ошибка в программе вызывает сбои для некоторой части входных данных; г) пропуск программы с некоторым подмножеством входных данных представляет собой единичное наблюдение действия. Для сокращения до минимума количества ошибок, встречающихся в программах, необходимо знание факторов, определяющих надежность ПО. Совокупность последних можно разделить на три группы: общие факторы; факторы, связанные с разработкой ПО; эксплуатационные факторы. К общим факторам относятся: • процедуры управления разработкой ПО; • подготовка управления разработкой ПО; • архитектура вычислительной системы; • языки программирования. К факторам, связанным с разработкой ПО, относятся: • конструктивные (разряды и стоимость разрабатываемой системы, структура построения программы, наличие опыта разработки, степень выполнения последовательности работ); • технологические (техника программирования); • организационные (управление надежностью в процессе разработки, степень обучения и информативности персонала, микроклимат в группе, выполняющей разработку, временные ограничения на выполнение работ). К эксплуатационным факторам относятся: • полнота и качество эксплуатационной документации; • степень адаптации документации; • простота изучения и использования системы ПО на основе документации и путем контрольных пропусков на ЭВМ; • качество обучения пользователей, ответственных за эксплуатацию ПО; • степень выполнения стандартов на эксплуатацию ПО; • защищенность информации программ. Для получения надежных программ необходимы твердые знания о типах встречающихся ошибок. Ошибки в ПО встречаются на всех этапах технологического процесса производства ПО, начинающегося с постановки задачи и заканчивающегося получением набора и дробных инструкций, управляющих действиями ЭВМ при обработке информации. Для достижения заданного уровня надежности ПО необходимо: • избегать ошибок, возникающих в процессе создания ПО; • обнаруживать ошибки; • исправлять допущенные ошибки; • предусматривать допуск ошибок. К средствам избегания ошибок в процессе проектирования относятся такие, целью которых является предупреждение появления ошибок в программе, а именно: • средства и приемы минимизации сложности как основной причины ошибок трансляции; • средства и методы совершенствования информационных связей разработчиков; • средства и приемы немедленного обнаружения и удаления ошибок трансляции после каждого ее шага, а не после завершения написания программы. К средствам обнаружения ошибок относятся: • организация проверки значений входных данных на известное ограничение; • проверка на совместимость входных данных; • введение необходимой избыточности входных данных; • организация сравнения входных данных с некоторым набором внутренних данных. МЕТОД НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА (ДЛЯ РАСЧЕТА РЕЗЕРВА). Состоит в следующем: для нахождения экстремума некой функции (m1,m2,....) при выполнении условия (m1,m2...) 0 составляется функция Лагранжа F(m1,m2,...) (m1,m2...) (m1,m2...) , где - неопределённый множитель. Необходимые условия экстремума функции выражаются системой уравнений 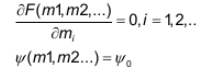 Система решений m1,m2… (в нашем случае это – кратности резервирования), удовлетворяющих этим уравнениям, может дать экстремум рассматриваемой функции. Система решений m1,m2… (в нашем случае это – кратности резервирования), удовлетворяющих этим уравнениям, может дать экстремум рассматриваемой функции.Нецелочисленные значения кратностей округляются в сторону ближайших целых чисел, часть которых исключается ввиду невыполнения для них требуемого условия. Подробно: https://math.semestr.ru/optim/method-lagrange.php Из методички: Для решения задачи оптимального резервирования используется метод неопределенных множеств Лагранжа: Необходимо найти: 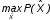 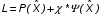 — неопределенный множитель Лагранжа; — ограничение. Решив систему уравнений, можно найти необходимое количество резервных элементов. 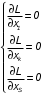 Метод не дает однозначного решения: аргументы будут нецелочисленными (надо округлять), ограничения заданы в виде строгого равенства, а надо больше или равно. Для устранения указанных недостатков решения задачи оптимального резервирования используется градиентный метод. Экстремум функции ищется из начальной точки по направлению градиента по шагам. Для оптимального резервирования на первом шаге отыскивается тот элемент системы, который дает наибольший прирост показателя надежности, на втором - элемент, у которого имеется максимальный прирост показателя надежности, включая уже зарезервированный, до тех пор, пока не выполниться ограничение (по стоимости). Метод называется покоординатным спуском, который является одним из самых простых методов поиска экстремума функции многих переменных (рис. 4.2). В литературе говориться, что данный метод может «застревать», когда линии уровня сильно вытянуты (см. рис. 4.2 б), т.е. пробные шаги во всех направлениях не приводят к уменьшению значения целевой функции, и процесс вычисления прерывается вдали от точки минимума.
Рис. 4.2 Поиск минимума функции двух переменных методом покоординатного спуска Но так как надо минимизировать функцию надежности системы 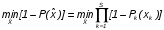 которая при всегда будет уменьшаться при увеличении количества резервных элементов, можно не усложнять алгоритм покоординатного спуска, например методом предложенным Хуком и Дживсом. ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ. В качестве единицы измерения для безотказности применяется - непрерывное время безотказной работы системы (наработка на отказ T’). Восстанавливаемые системы имеют поток отказов и периодически подвергаются воздействию системы технического обслуживания и ремонта. (рис.1.9), где  Рис.1.9. Процесс эксплуатации ti — i-ая наработка на отказ. ti — i-ое время восстановления после i-ого отказа Случайную величину длительности безотказной работы между соседними периодами восстановления системы можно характеризовать функцией распределения длительности безотказной работы между окончанием восстановления после (i-1)-го отказа и моментом наступления i-го отказа Fi(t). Тогда показатель Qi(t) = Fi(t) будет означать вероятность наступления отказа системы за промежуток времени t после окончания (i-1)-го восстановления. Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t: 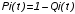 . .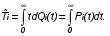 . .Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа: Toi Перечисленные показатели можно назвать локальными. Они характеризуют безотказность в интервалах времени между двумя соседними отказами. Частным случаем локальных показателей безотказности восстанавливаемых систем будут показатели безотказности невосстанавливаемых систем, если рассматривать свойства безотказности до первого отказа 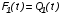 ; ; 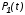 ; ; 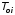 и т.д. и т.д. Для общего случая, который учитывает все отказы за интервал времени t, используются общие показатели безотказности, в частности ведущая функция потока отказов W(t) (математическое ожидание случайного числа отказов за время t): 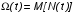 , ,где М – математическое ожидание; N(t) – случайное число отказов. Следующий общий показатель безотказности - параметр потока отказов (среднее значение количества отказов в единицу времени за рассматриваемый интервал времени - имеет вид 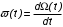 . .Справедливо обратное соотношение 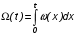 . .Наглядной характеристикой восстанавливаемых систем является среднее значение параметра потока отказов за рассматриваемую наработку TP: 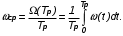 Среднюю наработку между отказами восстанавливаемого изделия характеризует показатель Т: 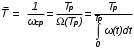 . .Предел параметра потока отказов 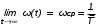 . .Показатель (t) связан с показателями невосстанавливаемых изделий f(t) и (t) неравенством 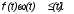 . .Если случайные величины наработки между отказами одинаково распределены и независимы (одинаковые законы распределения случайной величины наработки между отказами), т.е. F1(t) = F2(t) = … = Fk(t), то (t) связан с плотностью распределения наработки между отказами f(t) уравнением возобновления 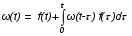 . .В некоторых случаях удобно искать решение преобразование Лапласа: 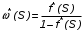 , ,где 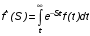 . .Если функция распределения наработки между отказами подчиняется экспоненциальному закону распределения, то расчет значительно упрощается. ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО РЕЗЕРВИРОВАНИЯ. Информационные системы состоят из отдельных элементов. Эти элементы с течением времени отказывают и заменяются резервными. Снятые с эксплуатации элементы подвергаются ремонту. Модель должна определять оптимальный уровень резервных элементов каждого типа. По условию задачи требуется, чтобы система функционировала с максимальной надежностью. Если какой-нибудь элемент отказывает, то его заменяют запасным из числа резервных. Отказавший элемент сразу начинают ремонтировать. В системе непрерывно должно функционировать 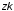 элементов элементов 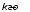 типа, причем в запасе должно иметься типа, причем в запасе должно иметься 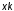 элементов того же элементов того же 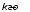 типа типа 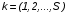 . .Сущность задачи заключается в оптимальном распределении стоимостных или каких-либо других ресурсов 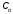 , выделенных на приобретение резервных единиц. , выделенных на приобретение резервных единиц.Рассматриваемая система считается отказавшей, если в момент отказа работающего элемента 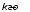 типа все типа все 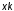 запасных элементов того же типа находятся в ремонте. Таким образом, надо найти количество резервных элементов запасных элементов того же типа находятся в ремонте. Таким образом, надо найти количество резервных элементов 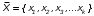 так, чтобы вероятность нехватки резервных элементов была минимальной. так, чтобы вероятность нехватки резервных элементов была минимальной.Введем обозначения: 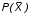 - показатель надежности всей системы (вероятность безотказной работы системы); - показатель надежности всей системы (вероятность безотказной работы системы);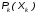 - вероятность безотказной работы - вероятность безотказной работы 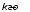 элемента. элемента.Так как модель соединений элементов с точки зрения надежности представляется как последовательное соединение элементов, то справедлива формула 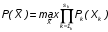 Можно сформулировать задачу на минимум: необходимо найти минимум риска нехватки элементов 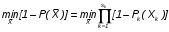 На все элементы есть ограничения (вес, цена, объем и т.д.). Но мы будем пользоваться только стоимостным ограничением, как, пожалуй, наиболее часто встречающимся, хотя задача решается и для нескольких ограничений. 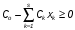 , ,где 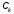 - стоимость одного элемента k-го типа. - стоимость одного элемента k-го типа. Подходы к решению задачи оптимального резервирования: 1) метод неопределенных множеств Лагранжа; 2) градиентный метод; 3) метод динамического программирования. ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ И РЕМОНТОПРИГОДНОСТИ. Показатели безотказности невосстанавливаемых систем В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t) , которая в данном случае будет называться функцией вероятности отказа Q ( t ), т.е.: 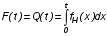 . .Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t: 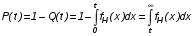 . .Графики, дающие представление о характерах изменения функций P(t) и Q(t), представлены на рисунке: 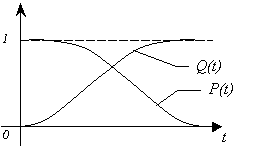 Рис.1.6. График изменения функций P(t) и Q(t) Плотность распределения вероятностей как показатель безотказности невосстанавливаемых систем принимает смысл плотности распределения наработки на отказ fH(t), а интенсивность (t) принимает смысл функции интенсивности отказов l(t): 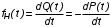 . . 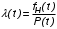 . . Между функциями P(t) и l(t) существует взаимосвязь: 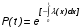 . . Взаимосвязь между функциями fH(t) и l(t) можно определить из соотношения: 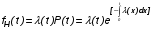 . .Если одна из четырех функций известна, то остальные три можно вычислить по формулам, приведенным в таблице. Удобный и наглядный физический смысл имеет показатель "средняя наработка на отказ", который равен математическому ожиданию времени исправной работы до первого отказа: 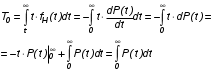 . .Свойства функции безотказной работы P(t): 1.При t=0, P(t)=1 , т.е. в нулевой момент времени система будет работоспособна. 2. P(t) — монотонно убывающая функция во времени. 3.При t→∞, P(t) → 0. Таблица 1.1. Взаимосвязь показателей безотказности невосстанавливаемых систем
На практике часто требуется определить показатели безотказности при том условии, что элемент, проработавший время t1, будет безотказно работать в течение промежутка времени от t1 до t2 (t2>t1). В этом случае основные показатели находятся как условные вероятности. Условная вероятность безотказной работы в течение наработки t = t2 - t1 (рис. 1.7) при условии, что система безотказно проработала от 0 до t1, равна: 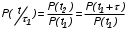 . .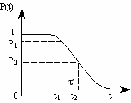 Рис.1.7. График условной вероятности работы системы Условная вероятность отказа равна: 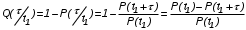 . . Условная интенсивность отказа равна: 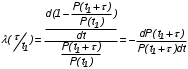 . . Условная наработка на отказ равна: 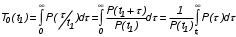 . . Теперь перейдем к рассмотрению статистических оценок показателей безотказности, которые в литературе обозначаются либо символом ^ либо *. Пусть на испытания было поставлено No систем, которые с течением времени отказывали, что модно представить временной диаграммой (No - количество изделий, n(t) - количество отказавших изделий за время t): 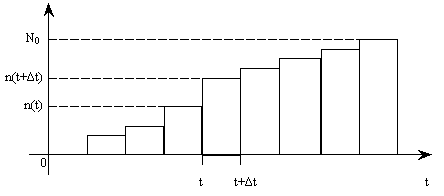 Рис.1.9. Результаты испытания No систем Показатели безотказности можно оценивать приближенно по статистическим данным. Рассмотрим формулы для определения статистических значений показателей безотказности. Статистическая оценка вероятности отказа: 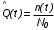 . .Статистическая оценка вероятности безотказной работы: 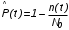 . .Статистическая оценка плотности распределения наработки на отказ: 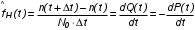 . .Статистическая оценка интенсивности отказов:  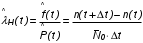 , ,где 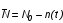 . .Статистическая оценка средней наработки на отказ находится по формуле: 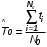 , , где ti — наработка на отказ i-й системы. Показатели безотказности восстанавливаемых систем Восстанавливаемые системы имеют поток отказов и периодически подвергаются воздействию системы технического обслуживания и ремонта. (рис.1.9), где  Рис.1.9. Процесс эксплуатации ti — i-ая наработка на отказ. ti — i-ое время восстановления после i-ого отказа Случайную величину длительности безотказной работы между соседними периодами восстановления системы можно характеризовать функцией распределения длительности безотказной работы между окончанием восстановления после (i-1)-го отказа и моментом наступления i-го отказа Fi(t). Тогда показатель Qi(t) = Fi(t) будет означать вероятность наступления отказа системы за промежуток времени t после окончания (i-1)-го восстановления. Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t: 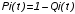 . .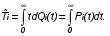 . .Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа: Toi Перечисленные показатели можно назвать локальными. Они характеризуют безотказность в интервалах времени между двумя соседними отказами. Частным случаем локальных показателей безотказности восстанавливаемых систем будут показатели безотказности невосстанавливаемых систем, если рассматривать свойства безотказности до первого отказа 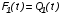 ; ; 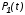 ; ; 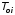 и т.д. и т.д. Для общего случая, который учитывает все отказы за интервал времени t, используются общие показатели безотказности, в частности ведущая функция потока отказов W(t) (математическое ожидание случайного числа отказов за время t): 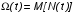 , ,где М – математическое ожидание; N(t) – случайное число отказов. Следующий общий показатель безотказности - параметр потока отказов (среднее значение количества отказов в единицу времени за рассматриваемый интервал времени - имеет вид 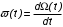 . .Справедливо обратное соотношение 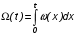 . .Наглядной характеристикой восстанавливаемых систем является среднее значение параметра потока отказов за рассматриваемую наработку TP: 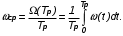 Среднюю наработку между отказами восстанавливаемого изделия характеризует показатель Т: 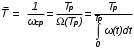 . .Предел параметра потока отказов 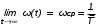 . .Показатель (t) связан с показателями невосстанавливаемых изделий f(t) и (t) неравенством 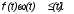 . .Если случайные величины наработки между отказами одинаково распределены и независимы (одинаковые законы распределения случайной величины наработки между отказами), т.е. F1(t) = F2(t) = … = Fk(t), то (t) связан с плотностью распределения наработки между отказами f(t) уравнением возобновления 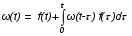 . .В некоторых случаях удобно искать решение преобразование Лапласа: 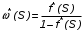 , ,где 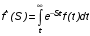 . .Если функция распределения наработки между отказами подчиняется экспоненциальному закону распределения, то расчет значительно упрощается. Показатели ремонтопригодности Свойство ремонтопригодности в принципе можно определять, как и все остальные свойства надежности, через соответствующие показатели, которые определяются через законы распределения длительности восстановления fв(t) и Fв(t). Из всей номенклатуры предлагаемых показателей для характеристики свойства ремонтопригодности применяют следующие: -интенсивность восстановления 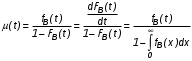 . .-среднее время восстановления 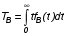 . .-и вероятность восстановления за заданное время 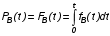 . .ПОКАЗАТЕЛИ ДОЛГОВЕЧНОСТИ И СОХРАНЯЕМОСТИ. Показатели долговечности В качестве случайных величин, характеризующих долговечность технических систем, применяют две: -ресурс - наработка системы до списания выраженная во временных единицах измерения без учета простоев; -срок службы - календарная продолжительность службы объекта до его списания. Считаются известными законы распределения случайной величины ресурса fр(t) и Fр(t) или случайной величины срок службы fсл(t) и Fсл(t). Рассмотрим наиболее употребимые показатели долговечности. 1) Средний ресурс или средний срок службы – математическое ожидание средней величины ресурса или срока службы совокупности изделий одного типа и исполнения: 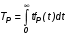 , ,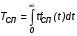 . .2) Гамма-процентный ресурс или срок службы, который имеют и превышают в среднем определенное число - процентов изделий Tрg, Tслg: 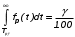 , ,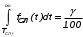 . .3) Медианный ресурс или срок службы Трм, Тслм: 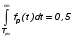 , ,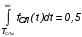 . .Показатели сохраняемости Определение свойств сохраняемости аналогично определению свойств безотказности с тем лишь различием, что они относятся к разным условиям: свойство безотказности характеризует рабочие эксплуатационные условия, а свойство сохраняемости – нерабочие условия (хранение и транспортировка). Показатели сохраняемости аналогичны показателям безотказности. Однако вычислять их нужно не через функции fн(t) и Q(t), а через законы распределения длительности безотказного хранения fхр(t) и Fхр(t). Срок сохраняемости – календарная продолжительность хранения или транспортировки изделия, в течение и после которой сохраняются значения показателей безотказности, долговечности и ремонтопригодности в установленных пределах. Из всего множества показателей сохраняемости наиболее часто в технической документации используют только два: средний срок сохраняемости и гамма-процентный срок сохраняемости. Средний срок сохраняемости — математическое ожидание случайной величины хранения до отказа: 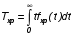 . .Гамма-процентный срок сохраняемости — срок сохраняемости, который достигается объектом с вероятностью g выраженной в процентах Tхр.: 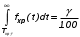 . .Рекомендуются значения = 90; 95 и 98%. Кроме того, применяют еще и медианный срок сохраняемости при = 50% Tхрμ: 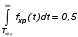 . .КОМПЛЕКСНЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ. Показатели, зависящие более чем от одного свойства, называются комплексными. Чаще всего комплексные показатели отражают два свойства надежности: безотказность и ремонтопригодность. К таким показателям относятся: -функции готовности и простоя; -коэффициенты готовности и простоя; -коэффициент технического использования; -коэффициент оперативной готовности. Функция готовности Кг(t) - вероятность того, что в любой произвольный момент времени система будет находиться в работоспособном состоянии. Функция простоя Кп(t) - вероятность того, что в произвольный момент времени система будет находиться в неработоспособном состоянии: Кп(t) = 1 - Кг(t). Функции готовности и простоя с течением времени эксплуатации стремятся к стационарному значению (рис.1.10). Предельное значение функции готовности называется коэффициентом готовности, а функции простоя – коэффициентом простоя: 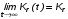 , ,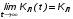 . .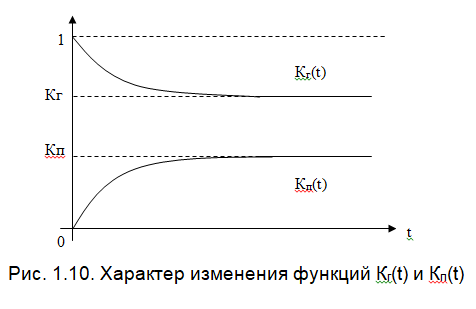 К 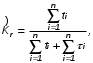 оэффициент готовности можно определить по статистическим данным: где ti - наработка на отказ; i - время восстановления после i-го отказа; n - число отказов за рассматриваемый период. Если разделить числитель и знаменатель правой части на n, то получим 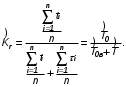 При n: 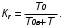 Аналогично определяется коэффициент простоя 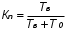 , ,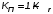 . .ГОСТ 27.002-89 дает уточненное определение коэффициента готовности, который определяется, как вероятность в произвольный момент времени застать систему в работоспособном состоянии, кроме периодов, предусмотренных на плановое техническое обслуживание и ремонт. Наряду с коэффициентом готовности, рекомендуется использовать коэффициент технического использования Кти. Коэффициент технического использования - отношение математического ожидания нахождения системы в работоспособном состоянии к сумме математических ожиданий нахождения системы в работоспособном состоянии и в неработоспособном с учетом плановых и неплановых перерывов. 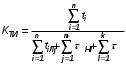 . .где tпi - время планового простоя, tнi - время непланового. Довольно широкое распространение получил еще один комплексный показатель надежности, который называется коэффициентом оперативной готовности Ког: 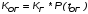 . .Коэффициент оперативной готовности определяет вероятность безотказного функционирования системы при выполнении ожидаемой задачи. По Ког – вероятность того, что система окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течении которых применение системы по назначению не предусматривается, и, начиная с этого момента будет работать безотказно в течение заданного интервала времени tог. ПОКАЗАТЕЛИ НАДЕЖНОСТИ СЛОЖНЫХ ОБЪЕКТОВ (ПРИ ПОСЛЕДОВАТЕЛЬНОМ И ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ). К классическим методам относятся модели надежности с последовательным, параллельным, параллельно-последовательным соединениями элементов, их различные модификации. Модель с последовательным соединением элементов (рис. 2.1). При расчетах надежности последовательным называется такое соединение элементов, при котором отказ хотя бы одного из них приводит к отказу всего соединения в целом. Последовательное соединение в указанном выше смысле не всегда совпадает с физическим последовательным соединением элементов. Отказы элементов предполагаются независимыми, то есть отказ любой группы элементов никак не влияет на вероятностные характеристики остальных элементов. Элемент понимается как один из самостоятельных участков последовательного соединения.  Рис. 2.1. Последовательное соединение элементов В данном случае вероятность безотказной работы системы можно рассчитать по формуле:  где Рс – вероятность безотказной работы системы; Рi(t) – вероятность безотказной работы i-го элемента системы Модель с параллельным соединением элементов (рис. 2.2). При расчетах надежности параллельным (резервным) называется такое соединение элементов, при котором отказ всего соединения происходит при отказе всех элементов системы (элементы дублируют друг друга). 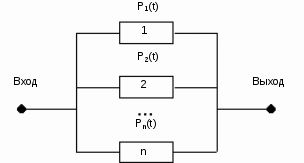 Рис. 2.2. Параллельное соединение элементов В этом случае показатель надежности системы Pc определяется через вероятности отказа элементов q1, q2, …, qn, которые связаны с вероятностью безотказной работы соотношениями вида qi(t) = 1 – Pi(t) Вероятность отказа всей системы равна: 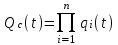 Тогда вероятность безотказной работы системы с параллельным соединением элементов q1, q2, …, qn имеет вид  . .ОПТИМАЛЬНОЕ РЕЗЕРВИРОВАНИЕ МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ. Для решения задачи оптимального резервирования используется метод динамического программирования(наряду с градиентным методом). В основе метода лежит пошаговый процесс, на каждом шаге строится доминирующая последовательность 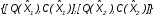 где переход в состояние с более высокой надежностью (или более низкой вероятностью отказа Q) происходит с минимальными затратами по стоимости C, здесь 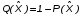 - риск нехватки резервных элементов. - риск нехватки резервных элементов.Доминирующая последовательность строится по следующему правилу 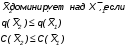 Алгоритм построения доминирующей последовательности состоит из шагов, на каждом из которых строится следующая таблица. Рассматриваем две подсистемы из 1-го и 2-го типа элементов. Характеристики элементов 1-го типа записываются в заголовках столбцов, а характеристики 2-го типа - в заголовках строк. На пересечении каждой строки и каждого столбца записываются суммы стоимостей C и вероятностей нехватки элементов q. (табл. 1). Таблица 1.
Вначале проводим анализ элементов таблицы по ограничениям. Вычеркиваем те элементы, которые имеют значение стоимости большее, чем ограничение по стоимости Co и, чем ограничение по вероятности нехватки элементов Qo. Делаем анализ на доминирование: рассматриваются оставшиеся клетки и сравниваем последовательно со всеми элементами (клетками). Если для каких-то двух векторов выполняется условие строгого доминирования, то т худший вычеркивается. Вектор X1 доминирует над вектором X2, если вероятность нехватки элементов P(X1) P(X2), а стоимость С(X1) С(X2) или вероятность нехватки элементов Q(X1) Q(X2) и стоимость С(X1) С(X2). Вектор X1 строго доминирует над вектором X2, если одно из перечисленных неравенств будет строгим. Все оставшиеся элементы переносим в заголовки столбцов, а в качестве заголовков строк будут выступать характеристики элементов третьего типа. Всего будет S-1 таблица, на последнем шаге вычислений ищется оптимальный вектор, у которого и будет минимальная вероятность отсутствия резервных элементов. Пример решения задач Передающее устройство состоит из четырех блоков (1, 2, 3 и 4). Вероятности отказов блоков равны: q1=0,02; q2=0,1; q3=0,08; q4=0,12, а величины затрат на каждый блок равны соответственно: с1=42; с2=63; с3=10; с4=12. Требуется определить оптимальный состав устройства, который может быть получен путем введения нагруженного резерва при условии, что вероятность отказа устройства – величина q ≤ Q0; а затраты на каждый блок - с ≤ С0, причем Q0=0,08; С0=300. Оптимальный состав устройства определим методом динамического программирования. В основе решения лежит пошаговый процесс. На каждом шаге строится матрица, в которой рассматриваются все возможные варианты и вычеркиваются заведомо неперспективные варианты. Все множество допустимых решений будет представлять доминирующую последовательность. При построении доминирующей последовательности используем условие доминирования: 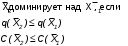 На первом шаге строим таблицу (табл. 2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 (t)
(t)