метод количественного анализа. ККЗ_МКА_Фомина СИ_ДО-308МВА. Московский финансовопромышленный университет Синергия

Название	Московский финансовопромышленный университет Синергия
Анкор	метод количественного анализа
Дата	24.06.2022
Размер	0.51 Mb.
Формат файла
Имя файла	ККЗ_МКА_Фомина СИ_ДО-308МВА.doc
Тип	Программа #613782
страница	3 из 3

1 2 3

Основные статистические характеристики переменных

Цена	Относит. частота	Накопл. частота	Калории	Относит. частота	Накопл. частота	Жир	Относит. частота	Накопл. частота
≥0,54	2,78	2,78	≥280	2,78	2,78	≥4	2,78	2,78
≥0,77	8,33	11,11	≥302	8,33	11,11	≥7,67	2,78	5,56
≥1	44,44	55,56	≥324	11,11	22,22	≥11,33	11,11	16,67
≥1,23	8,33	63,89	≥346	25,00	47,22	≥15	33,33	50,00
≥1,46	22,22	86,11	≥368	16,67	63,89	≥18,67	16,67	66,67
≥1,69	5,56	91,67	≥390	19,44	83,33	≥22,33	22,22	88,89
≥1,92	8,33	100,00	≥412	16,67	100,00	≥26	11,11	100,00
Итого	100			100			100

На основе таблицы по каждой переменной построены кривую распределения (полигоны накопленных частот). Они показаны на рисунках

Проверим, есть ли связь между ценой пиццы и видом, к которому она относится (Cheese, Pepperoni или Chain). Так как один из показателей является количественным, а другой – качественным, будем использовать метод сопряженных таблиц, аналогичный примененному в задаче 3.

Выдвигаем гипотезы.

Основная гипотеза Н₀: рассматриваемые признаки независимы.

Альтернативная гипотеза Н₁: цена и вид зависимы.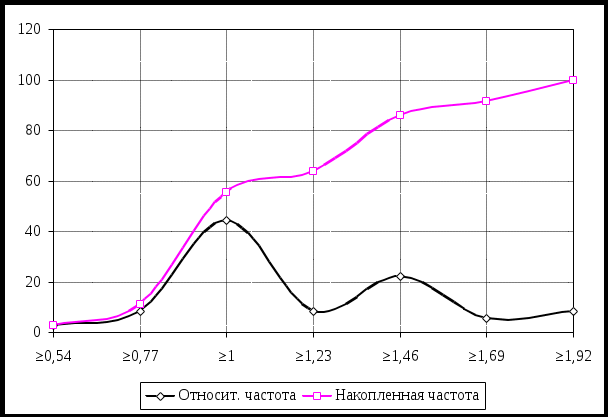

Рис. 1 − Цена: относительная и накопленная частота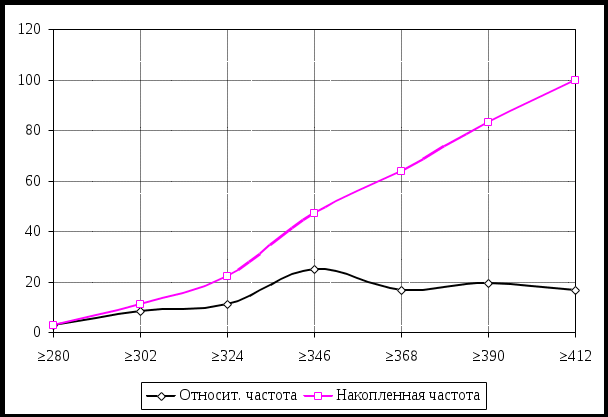

Рис. 2 − Калорийность: относительная и накопленная частота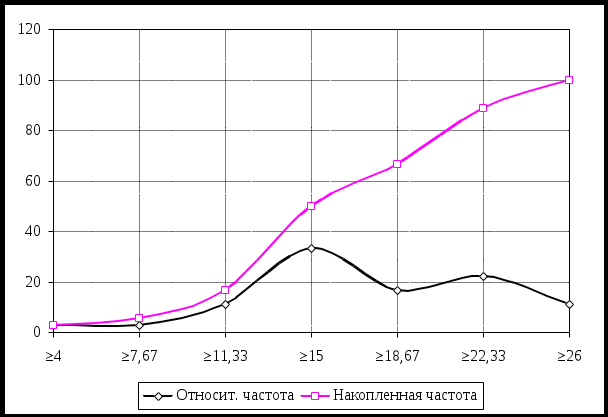

Рис. 3 − Жирность: относительная и накопленная частота

Таблица сопряженности с фактическими и теоретическими частотами представлена ниже

К расчету зависимости вид − цена. Фактические и теоретические частоты

Фактические частоты
	0,54 − 0,77	0,77 − 1,00	1,00 − 1,23	1,23 − 1,46	1,46 − 1,69	1,69 − 1,92	Итого
Cheese	2	10	2	2		1	17
Pepperoni	2	6		2	2		12
Chain				5		2	7
Итого	4	16	2	9	2	3	36
Теоретические частоты
	0,54 − 0,77	0,77 − 1,00	1,00 − 1,23	1,23 − 1,46	1,46 − 1,69	1,69 − 1,92	Итого
Cheese	1,89	7,56	0,94	4,25	0,94	1,42	17
Pepperoni	1,33	5,33	0,67	3,00	0,67	1,00	12
Chain	0,78	3,11	0,39	1,75	0,39	0,58	7
Итого	4	16	2	9	2	3	36

расчет теоретических частот проводился по формуле (1). Расчет значения

представлен в табл
К расчету зависимости вид − цена. Значение

№	f₀	f_E	f₀ − f_E	(f₀ − f_E)²
1	2	1,89	0,11	0,01	0,01
2	2	1,33	0,67	0,44	0,33
3	0	0,78	-0,78	0,60	0,78
4	10	7,56	2,44	5,98	0,79
5	6	5,33	0,67	0,44	0,08
6	0	3,11	-3,11	9,68	3,11
7	2	0,94	1,06	1,11	1,18
8	0	0,67	-0,67	0,44	0,67
9	0	0,39	-0,39	0,15	0,39
10	2	4,25	-2,25	5,06	1,19
11	2	3,00	-1,00	1,00	0,33
12	5	1,75	3,25	10,56	6,04
13	0	0,94	-0,94	0,89	0,94
14	2	0,67	1,33	1,78	2,67
15	0	0,39	-0,39	0,15	0,39
16	1	1,42	-0,42	0,17	0,12
17	0	1,00	-1,00	1,00	1,00
18	2	0,58	1,42	2,01	3,44
Сумма					23,46

Получаем

Учитывая количество строк в таблицах сопряженности, равное 3, и количество столбцов, равное 6, получаем количество степеней свободы df = (3 − 1) · (6 − 1) = 10. Принимаем α = 0,05.

Получаем

Гипотеза H₀ отвергается. Принимается гипотеза H₁: между видом пиццы и ее ценой есть статистически значимая связь.

Анализ таблицы сопряженности позволяет утверждать, что пицца Cheese самая дешовая, Pepperoni несколько дороже и Chain − самая дорогая.

Проверим теперь наличие связи между калорийностью и жирностью. Так как оба эти показателя количественные, будем использовать инструмент «Регрессия» из Анализа данных Excel.

После проведения расчетов был получен результат, изображенный на рис.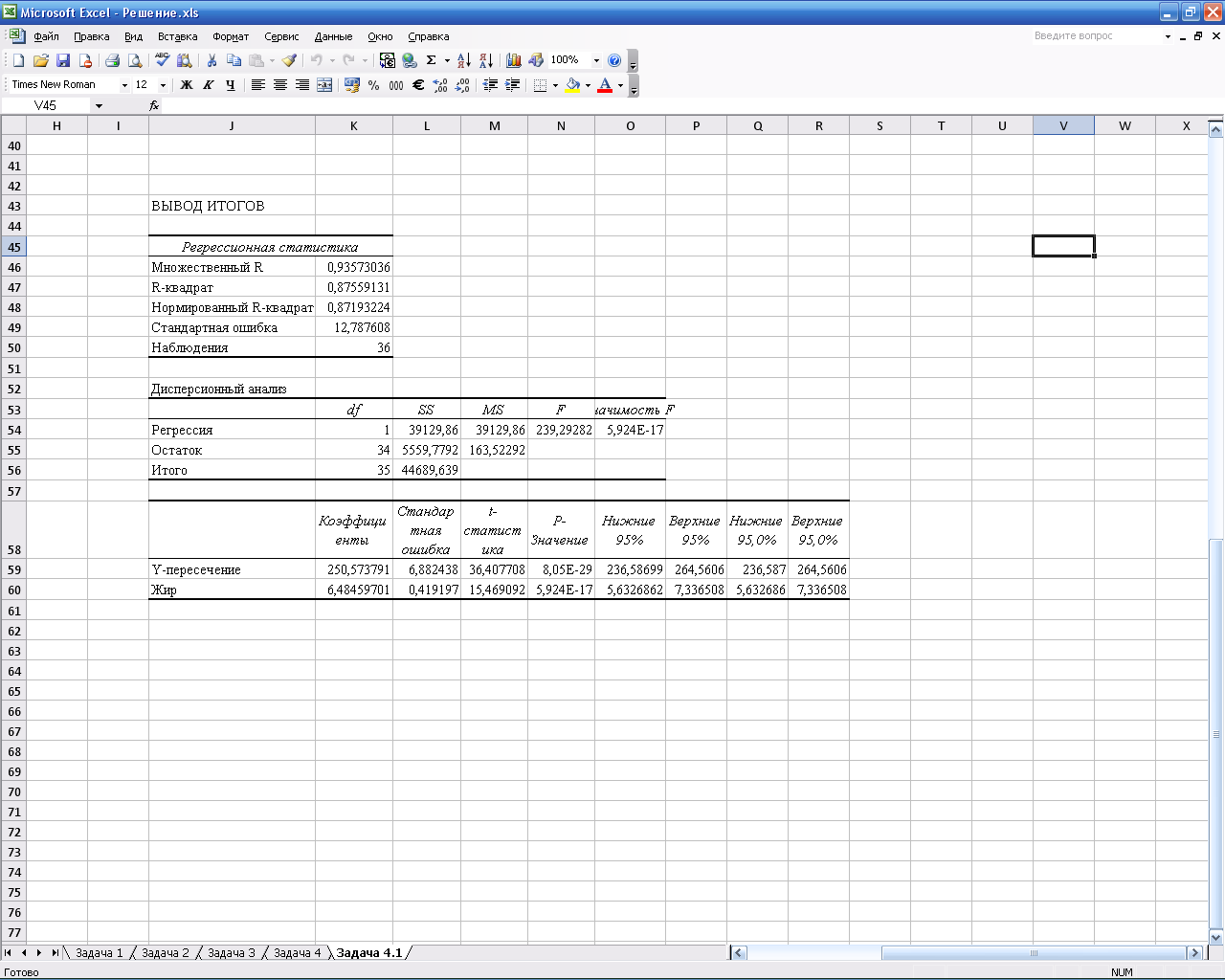

Рис. − Жирность: относительная и накопленная частота

В первую очередь обратим внимание на столбец «Коэффициенты», в нем представлены параметры полученного уравнения регрессии:

. Их можно интерпретировать следующим образом. Пицца, не содержащая жира, будет иметь калорийность 250,57. Каждый дополнительный грамм жира будет добавлять 6,48 единиц калорийности.

Построенная модель имеет достаточно высокое значение коэффициента детерминации (R-квадрат) − 0,8755. Это значит, что более 87% дисперсии результативного признака объясняется влиянием независимой переменной.

Адекватность модели можно определить по значению критерия Фишера F и его значимости (Значимость F) Так как значение F больше критического, а Значимость F много меньше α = 0,05, модель можно считать адекватной и значимой .

Вывод о статистической значимости коэффициентов уравнения можно сделать на основе сравнения t-статистик (критерий Стьюдента) с табличными и учитывая P-значения, которые так же меньше α = 0,05.

Проведенное исследование позволяет утверждать, что между типом пиццы и ценой, а так же между калорийностью и жирностью существует устойчивая статистически значимая связь.

1 2 3