Лекции радиотехника и электротехника. ЛЕКЦИИ_КОЛОДЕЖ_ЮВ_Электротехника_и_электроника. Москва 2012 Содержание

• Название: Москва 2012 Содержание
• Анкор: Лекции радиотехника и электротехника
• Дата: 26.11.2022
• Размер: 4.47 Mb.
• Имя файла: ЛЕКЦИИ_КОЛОДЕЖ_ЮВ_Электротехника_и_электроника.doc
• Тип: Лекция; #814027
• страница: 10 из 14

Лекция 8

НЕЛИНЕЙНЫЕ ЦЕПИ И ИХ РАСЧЕТ

В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики (ВАХ) линейных элементов (графическое изображение закона Ома) являются прямыми линиями.

Если электрическая цепь содержит, хотя бы один нелинейный элемент, она будет нелинейной. В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения. Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат. Например, только что рассмотренные диоды и транзисторы имеют несимметричные вольтамперные характеристики.

Важным понятием в вольтамперных характеристиках является понятие «Рабочая точка». Это точка «а» (на рисунках 43 и 44), положение которой задаётся значением аргумента. У нелинейных элементов выделяют два вида сопротивления: статическое, это сопротивление характеризует статику, то есть когда рабочая точка не перемещается по кривой ВАХ, и дифференциальное сопротивление, меняющееся из-за перемещения рабочей точки.

Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока (рис. 43). Это сопротивление пропорционально тангенсу угла наклона «α» между осью тока и прямой, проведенной из начала координат в рабочую точку характеристики. Статическое сопротивление как бы выпрямляет нелинейный элемент, делая его линейным.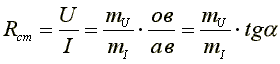

 



где 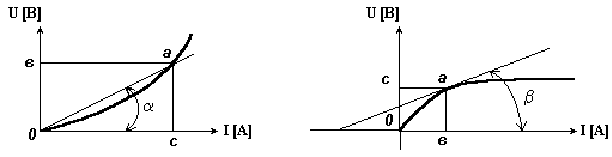- масштаб тока и напряжения на графике



Рисунок 43 Рисунок 44

Дифференциальное или динамическое сопротивление нелинейного элемента - это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока (рис. 44). При переходе к бесконечно малым получаем производную, то есть скорость изменения сопротивления.

Это сопротивление пропорционально тангенсу угла наклона «β» между осью тока и касательной к рабочей точке характеристики.



При переходе от одной точки вольтамперной характеристики к соседней статическое и дифференциальное сопротивления нелинейного элемента меняются.

Расчет электрических цепей с полупроводниковыми диодами.

На практике расчет сложных цепей с нелинейным элементом выполняется по методу Эквивалентного генератора, и в конце получается цепь, соответствующая схеме на рис. 45.

В практических схемах в цепь диода включается какая-либо нагрузка, например резистор (рис. 45 а). Прямой ток проходит тогда, когда анод имеет положительный потенциал относительно катода.

Режим диода с нагрузкой называют рабочим режимом. Если бы диод обладал линейным сопротивлением, то расчет тока в подобной схеме не представлял бы затруднений, так как общее сопротивление цепи равно сумме сопротивления диода постоянному току 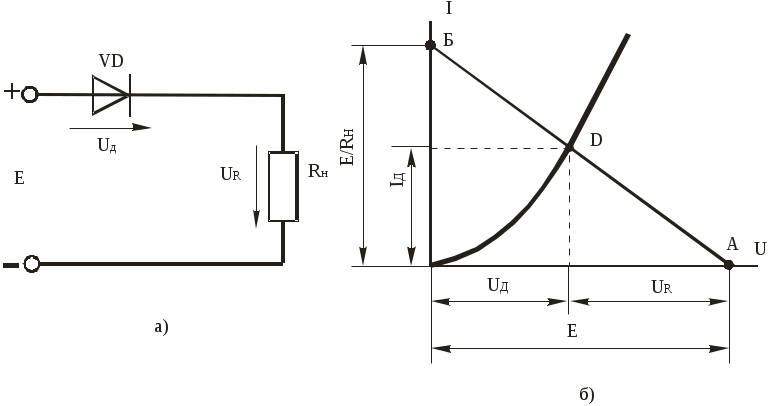и сопротивления нагрузочного резистора . Но диод обладает нелинейным сопротивлением, и значение у него изменяется при изменении тока. Поэтому расчет тока делают графически. Задача состоит в следующем: известны значения Е, и характеристика диода, требуется определить ток в цепи I и напряжение на диоде Uд.


Рисунок 45

Построение нагрузочной прямой
Характеристику диода следует рассматривать как график некоторого уравнения, связывающего величины I_д и U_д. А для сопротивления R_н подобным уравнением является закон Ома для участка R_н:



Итак, имеются два уравнения с двумя неизвестными I и U, причем одно из уравнений дано графически (характеристика нелинейного элемента). Для решения такой системы уравнений надо построить график второго уравнения и найти координаты точки пересечения двух графиков. Для этого рассмотрим все режимы работы нелинейного элемента – от его короткого замыкания, когда его сопротивление равно нулю, до холостого хода, когда цепь разорвана, и ток равен нулю.

При I = 0 (холостой ход) из уравнения получаем: Е − U_д = 0 или U_д = Е, то есть напряжение на нелинейном элементе равно Е, что соответствует точке А (с координатами Е и 0) на рис. 45, б. А если U_д = 0, (короткое замыкание нелинейного элемента, то есть, ток через нелинейный элемент не проходит и не создаёт падение напряжения на нем), то I = E/R_н. откладываем этот ток на оси ординат (точка Б). через точки А и Б проводим прямую, которая называется нагрузочная прямая, так как охватывает все режимы работы нелинейного элемента. Координаты точки D (рабочая точка нелинейного элемента – диода) дают решение поставленной задачи (смотри рисунок 45,б).