Методика изучения тригонометрических функций. Мотивация расширения области определения тригонометрических функций может быть осуществлена следующим образом
 Скачать 1.98 Mb.
|
 Мотивация расширения области определения тригонометрических функций может быть осуществлена следующим образом. Учитель напоминает учащимся, что им уже известны некоторые зависимости между сторонами треугольника: 1) в любом треугольнике каждая сторона меньше суммы двух других сторон; 2) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов. Возникает вопрос. Нельзя ли так же определённо, как и для прямоугольного треугольника, выразить зависимость между сторонами любого треугольника? Такая зависимость существует. Однако для се выявления необходимо расширить понятие косинуса острого угла на любой угол от 0° до 180°. Визуализация поднимает мотивацию учащихся при изучении любой темы. Чем сильнее будет образ, чем активнее проделана над ним работа учащихся, тем осмысленнее будет восприниматься само. У  каждого человека более или менее развиты слуховая, зрительная, образная., моторная память, оперативная память. Можно стараться подбирать опоры на "слух", "образ", "зрение". А теперь пример на развитие моторной и оперативной памяти. Одним из важных вопросов "Тригонометрии" является знание значений "хороших" углов: 00, 300, 450, 600, 900. И если "Математику надо знать как свои пять пальцев", то используем эти пальцы. Ни карандаш, ни бумага не нужны, а только левая ладонь.Каждому пальцу соответствует "хороший" угол. Мизинцу - 00 Безымянному - 300 Среднему - 450 Указательному - 600 Большому - 900 Учащимся необходимо помнить только, что любая функция - это отношение. "До" - количество пальцев снизу, "после" - сверху. Повысить мотивацию при изучении тригонометрии можно с помощью истории, а точнее исторической справки по теме. Слово «тригонометрия» состоит из двух греческих слов: «тригонон» — треугольник и «метрайн» — измерять. В буквальном смысле «тригонометрия» означает «измерение треугольников». Как и всякая наука, тригонометрия возникла из потребностей жизни. Развитие мореплавания требовало умения определять положение корабля в открытом море по солнцу и звездам. Войны, которые правители вели между собой, требовали умения определять большие расстояния и составлять карты местности. Землепашцу надо было знать смену времен года, чтобы своевременно производить необходимые сельскохозяйственные работы; лицам, связанным с исполнением религиозных обрядов, необходимо определять дни праздников и т. д. Повседневная жизнь становилась немыслима без календаря. Все это и многое другое привело к необходимости развивать астрономию — науку о движении небесных светил, а развитие астрономии было немыслимо без развития тригонометрии. Астрономия, а вместе с ней и тригонометрия возникли и развивались у народов с развитой торговлей и сельским хозяйством: у вавилонян, греков, индийцев, китайцев. Зародилась она много веков назад. Об этом мы можем судить не только по догадкам, но и изучая письменные памятники древности. Названия тригонометрических функций сложились исторически на протяжении ряда веков. Слово «синус» индийского происхождения. Полную хорду индийцы называли «лжива», т. с. тетива лука. Позднее при переводах с индийского на арабский и с арабского на латинский язык подлинный смысл слова был искажен. Понятия «косинус дуги», «тангенс дуги», «котангенс дуги» и другие впервые встречаются в книге «Шакл ул - Гита» знаменитого азербайджанскою ученого Насирэддина Т у с и. У него встречаются только соответствующие понятия, современных же терминов он не употребляет. Термины «косинус», «котангенс» и др. появились в XI—XVII вв. Например, синус угла, дополняющий данный до 90°, называли «синусом дополнения» (по-латыни sinus complement). В дальнейшем этот символ претерпел такие изменения: sinus со, со. — sinus. В 1600 г. английский ученый Э. Г ё н т е р употребил впервые слово «cosinus», а в 1748 г. Эйлер впервые употребил современную запись cos х. Сирийский ученый ал-Б а т т а н и (X в.) первым пришел к выводу, что острый угол в прямоугольном треугольнике можно определить отношением одного катета к другому. Слово «тангенс» (касающийся) взято из латинского языка, в Европе введено Томасом Финком в 1583 г.  Проследите последовательность изучения тригонометрического материала В учебнике Мордковича: функции → уравнения → преобразования В учебнике Алимова: преобразования → уравнения →функции Определения: В учебнике Алимова: «Синусом угла a называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол α». В учебнике Мордковича: «Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t, а ординату точки М называют синусом числа t». Эти два определения, принципиально не различаются, за исключением того, что у Алимова тригонометрические функции определяются как функции углового аргумента, а у Мордковича как функции числового аргумента.\ Особенности изложения материала в учебнике Мордковича В учебнике Мордковича рассматриваются две математические модели: «числовая окружность» и «числовая окружность на координатной плоскости». То есть учащиеся обучаются работать одновременно в двух системах координат: в прямоугольной и криволинейной. Это поможет, когда понятия синуса и косинуса угла будут вводиться через координаты. Неплохо в учебнике мотивируется и само введение числовой окружности: «В реальной жизни двигаться приходится не только по прямой, но и по окружности. Будем считать беговую дорожку стадиона окружностью…». В учебнике проводится хорошая пропедевтическая работа для введения тригонометрических функций. Особенности изложения материала в учебнике Алимова В учебнике Алимова для 9 класса тригонометрическим функциям и соотношениям между сторонами и углами треугольника посвящена отдельная глава . Синус угла а (0 <ог< 180') вводится здесь как ордината у точки М переченья луча И, образующего с положительной полуосью абсцисс угол а, и единичной полуокружности; косинус угла - абсцисса х точки М. Определение синуса и косинуса угла а в учебнике являются генетическими определениями: вначале разъясняется происхождение точки М, а затем говорится, что «синусом угла «называется ордината у точки М, косинусом угла - абсцисса * точки М».     На основе нескольких учебников был составлен перечень свойств тригонометрических функций. Наиболее удобным и наглядным способом доказательства, несомненно, является геометрический способ, основанный на изучении графиков функций. Свойства функции y = sin х: 1. Функция y=sinх нечетная, так как sin(−х) = − sin х. Функция y=sin х периодическая с главным периодом T= 2π, т.е. sin (х+2π)= sin х. Функция y = sin х непрерывна на промежутке (- ∞ ; + ∞). График функции пересекает ось Ох при х = πk, k ∈ Z. Промежутки знакопостоянства: y > 0 при (0+2πk; π+2πk), k ∈ Z и y < 0 при (π+2πk; 2π+2πk), k ∈ Z. Функция y=sinх возрастает на каждом из промежутков [−  +2πk;  +2πk], k ∈ Z и убывает на каждом из промежутков [ +2πk; +2πk], k ∈ Z.Минимум функции при х = − + 2πk, k∈Z, а максимум при х= + 2πk, k∈Z.График функции y = sinх - синусоида: 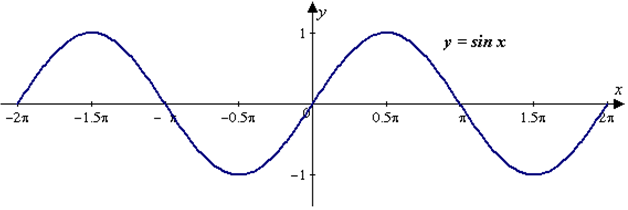 Функция y = cos х. Если каждому действительному числу х поставлено в соответствие число у, равное косинусу угла в х радиан, то говорят, что этим определена функция y = cos х называемая косинусом числового аргумента х. D(y)=R; E(y) = [−1;1]. Свойства функции y = cos х: Функция y= cos х четная, так как cos(−х) = cos х. Функция y=cosх периодическая с главным периодом T= 2π, т.е. cos(х+2π)= cosх. Функция y=cosх непрерывна на промежутке (- ∞ ; + ∞). График функции пересекает ось Ох при х= +πk, k∈Z.Промежутки знакопостоянства: y > 0 при (− +2πk; +2πk), k ∈ Z и y < 0 при ( +2πk;  +2πk), k ∈ Z.Функция y=cosх возрастает на каждом из промежутков [−π+2πk;2πk], k∈ Z, и убывает на каждом из промежутков [2πk;π+2πk], k∈ Z. Минимум функции при х=π+2πk, k ∈ Z, а максимум при х=2πk, k∈ Z. График функции y = cos α - косинусоида: 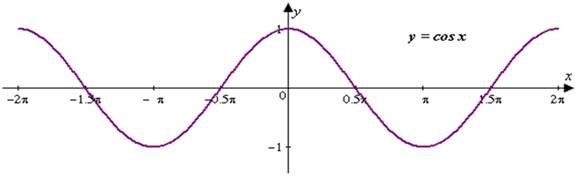 Функция y = tg х. Если каждому действительному числу х, отличному от х= +πk, где k-любое целое число, поставлено в соответствие число у, равное тангенсу угла в х радиан, то говорят, что этим определена функция y = tg х, называемая тангенсом числового аргумента х. D(y)=R, исключая числа х=  + πk, где k ∈ Z; E(y) = (- ∞ ; + ∞).Свойства функции y = tg х: Функция y= tgх нечетная, так как tg(−х)=−tg х. Функция y=tgх периодическая с главным периодом равным T= π, т.е. tg(х+π)=tg(х). Функция y=tg х непрерывна на каждом интервале (− +πk; +πk), k ∈ ZГрафик функции пересекает ось Ох при х=πk, k ∈ Z. Промежутки знакопостоянства: y > 0 при (πk; +πk), k ∈ Z и y < 0 при (− +πk; πk), k ∈Z.Функция y=tg х возрастает на каждом интервале (− +πk; +πk), k ∈ Z.График функции y= tgх - тангенсоида: 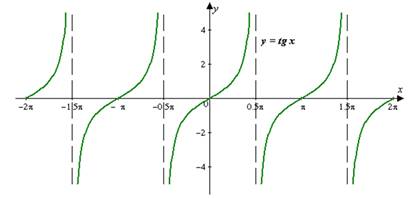 Функция y = сtg х. Если каждому действительному числу х, отличному от х=πk, где k ∈ Z, поставлено в соответствие число у, равное котангенсу угла в х радиан, то говорят, что этим определена функция y = сtg х, называемая котангенсом числового аргумента х. D(y)=R, исключая числа х= πk, где k ∈ Z; E(y) = (- ∞ ; + ∞). Свойства функции y = сtg х: Функция y=ctgх нечетная, так как ctg(−х)=−ctg х. Функция y=ctgх периодическая с главным периодом равным T= π, т.е. ctg(х+π)=ctg(х). Функция y=ctgх непрерывна на каждом интервале (πn; π+πk), где k∈Z.. График функции пересекает ось Ох при х= +πk, k ∈ Z.Промежутки знакопостоянства: y > 0 при (πk;  + πk), k ∈ Z и y < 0 при ( +πk; π+πk), k ∈Z.Функция y=ctg x убывает на каждом интервале (0+πk; π+πk), k ∈Z. График функции y= сtgх - котангенсоида: 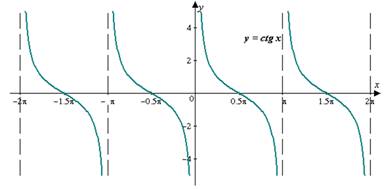  Рассмотрим построение графика тригонометрической функции на примере построения синусоиды. Аналогично построению любого графика функции в системе координат, график синусоиды строится по точкам, полученным путем подстановки значений х в формулу y= sinх. Алгоритм построения графика синусоиды: 1  . Строим особую систему координат.2. Выбираем масштаб по оси Ох, который равен 2π , что приближенно равно 12 клеточкам, а по оси Оу 2 клеточки=1единичный отрезок. 3. Находим значение функции, если вместо аргумента х подставить 0; π /2; 3 π /2; π; 2 π и т.д. (в принципе, можно сразу использовать соответствующие табличные значения). 4. Затем, наносим основные точки на координатную плоскость. При этом помним, что функция нечетная и график симметричен началу отсчета. Последовательно соединяем точки плавной линией. Получаем кривую, которая является «синусоидой». Для исследования свойств этой кривой полученного отрезка [0;2п], в принципе, вполне достаточно. 5. Так как функция y= sinх периодическая и Т=2π , то через интервал 2π значения функции повторяются и можно продолжать волну синусоиды до бесконечности. 6. Если нужно построить более точный график, то можно взять больше точек, например π/6; π /3; π/4 и т.д. Рассмотрим альтернативный способ первичного построения графиков тригонометрических функций. Окружность разделим на 12 частей. Пронумеруем точки указанным способом, т.е. 1 соответствует π/6 ; 2 соответствует π /3 ; 3 соответствует π /2 и т.д. Измерим длину дуги на окружности. Отложим на прямой между точками 1 и 2 соответствующее расстояние. Затем отметим точку на пересечении соответствующих чисел, т.е. точка находится под таким же номером, как и на окружности. Все полученные точки последовательно соединяем плавной сплошной линией. Получим искомую синусоиду. 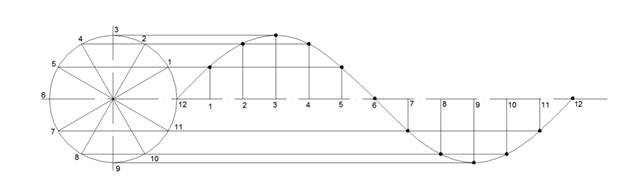     |