Реферат по геодезии. Работа. Постановка задачи и исходные данные
 Скачать 177.21 Kb. Скачать 177.21 Kb.
|
|
Задание № 1 Вычисление средних геоцентрических координат ИСЗ в системе координат стандартной эпохи по его истинным топоцентрическим координатам, заданным в системе координат эпохи наблюдения. Постановка задачи и исходные данные Из обработки наблюдений искусственного спутника Земли на момент всемирного координированного времени UТС𝑠 = 19ℎ 01𝑚 56,511𝑠 получены истинные топоцентрические координаты ИСЗ (прямое восхождение, склонение, расстояние до спутника) 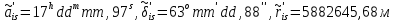 в системе координат эпохи наблюдения. В нашем случае: 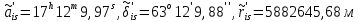 Требуется вычислить средние геоцентрические координаты ИСЗ (𝛼𝑠 , 𝛿𝑠, 𝑟𝑠), соответствующие положению средней точки весеннего равноденствия в стандартную эпоху J2000.0. Геодезические координаты (геодезическая широта, геодезическая долгота, геодезическая высота) 𝐵𝑖 = 44𝑜𝑑𝑑′𝑚𝑚,00′′, 𝐿𝑖 = 2ℎ 𝑚𝑚𝑚 𝑑𝑑,867𝑠, 𝐻𝑖 = 253,7 м. В нашем случае 𝐵𝑖 = 44𝑜12′9,00′′, 𝐿𝑖 = 2ℎ 9𝑚 12,867𝑠 пункта земной поверхности заданы относительно референц-эллипсоида с параметрами (большая полуось и сжатие) 𝑎𝑒 = 6378245 м, 𝑓 = 1/298,3 = 0,00335. Координаты центра референц-эллипсоида Δ𝑋0 = 25,0 м , ΔY0 = −141,0 м, ΔZ0 = −80,0 м в системе координат общего земного эллипсоида, ориентировка осей координат референцной системы 𝜀𝑥 = 0,10′′ , 𝜀𝑦 = 0,35′′ , 𝜀𝑧 = 0,66′′ относительно системы координат общего земного эллипсоида и масштабный коэффициент 𝛽0 = 2,5∙10−7 заданы. Координаты мгновенного полюса 𝑥𝑝 =−0,0132′′ , 𝑦𝑝 = 0,1664 ′′. относительно Международного Условного Начала и поправка за переход от всемирного согласованного времени к всемирному времени ∆𝑈Т1 =−0,3994𝑠 известны. Решение: 1. Вычисляем координаты вектора пункта i в референцной системе координат  где  – радиус кривизны первого вертикала, – радиус кривизны первого вертикала, 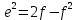 – квадрат первого эксцентриситета. – квадрат первого эксцентриситета.Определяем: 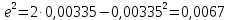    2. Вычисляем координаты вектора пункта i в средней общеземной системе координат   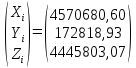 3. Вычисляем координаты вектора пункта i в мгновенной общеземной системе координат 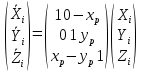 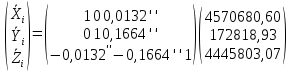 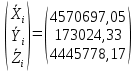 4. Вычисляем составляющие нутации в долготе ∆𝜓 и наклонности ∆𝜓= −17,21′′ sin𝐹5 + 0,003′′ cosF5 −1,32′′sin2(𝐹3 − 𝐹4 + 𝐹5) − 0,23′′ sin 2(𝐹3 + 𝐹5 ) +0,21′′ sin 2𝐹5 + 0,15′′ sin 𝐹2 − 0,05′′ sin(𝐹2 + 2𝐹3 − 2𝐹4 + 2𝐹5 ) + 0,07′′ sin 𝐹1 ; ∆𝜀= 9,21 ′′ cos 𝐹5 + 0,002′′ sin𝐹5 + 0,57′′ cos 2(𝐹3 − 𝐹4 + 𝐹5) + 0,10′′ cos 2(𝐹3 + 𝐹5 ) −0,09′′ cos 2𝐹5 + 0,01′′ cos 𝐹2 + 0,02′′ cos(𝐹2 + 2𝐹3 − 2𝐹4 + 2𝐹5), где 𝐹𝑖 - фундаментальные аргументы Делоне 𝐹1 ≡ 𝑙= 134,96340251𝑜 + 1717915923,2178 ′′𝑡+ 31,8792′′ 𝑡2 + 0,051635′′ 𝑡3 −0,00024470′′ 𝑡4 ; 𝐹2 ≡ 𝑙′ = 357,52910918𝑜 + 129596581,0481′′ 𝑡− 0,5532′′ 𝑡2 + 0,000136′′ 𝑡3 − 0,00001149′′ 𝑡4 𝐹3 ≡ 𝐹= 93,272090062𝑜 + 1739527262,8478′′ 𝑡− 12,7512′′ 𝑡2 − 0,001037′′ 𝑡3 +0,00000417′′ 𝑡4 ; 𝐹4 ≡ 𝐷= 297,85019547𝑜 + 1602961601,2090′′ 𝑡− 6,3706′′ 𝑡2 + 0,006593′′ 𝑡3 −0,00003169′′ 𝑡4 ; 𝐹5 ≡ Ω = 125,04455501𝑜 − 6962890,5431′′ 𝑡+ 7,4722′′ 𝑡2 + 0,007702′′ 𝑡3 − 0,00005939′′ 𝑡4; 𝑡= (𝐽𝐷− 2451545,0) / 36525 - промежуток времени в юлианских столетиях от стандартной эпохи до момента наблюдений; 𝐽𝐷= 1721013,5 + 367 ∙ 2022 – 𝐸{7[2022 + 𝐸((9+ 9)/12)]/4} + 𝐸(275 ∙ 9/9) +12+ (𝑈T1)𝑑 - юлианская дата, 𝐸(𝑥) - целая часть числа x; 𝑈T1 = 𝑈TC+ ∆𝑈T1 - момент Всемирного времени. Вычислим неизвестные величины: 𝑈T1 = = 19ℎ 012 56,511𝑠 −0,3994𝑠 = 19ℎ 012 56,112𝑠 𝐽𝐷= 1721013,5 + 367 ∙ 2022– 𝐸{7[2022 + 1*0,917]/4} + 𝐸(275 ∙ 9/9) +12 – 0,3994 =1721013,5+742074-3540+275+12-0,3994 =2464654,7 𝑡= (2464654,7− 2451545,0) / 36525 = 0,36 𝐹1 ≡ 𝑙= 134,96340251𝑜 + 1717915923,2178′′ *0,36 + 31,8792′′*0,362 + +0,051635′′*0,363 −0,00024470′′ *0,364 =134,96340251𝑜 + 618449732.3584′′+4,1315′′+0,0024′′-4,1*10-6 = 135° 4’ 35” 𝐹2 ≡ 𝑙′ = 357,52910918𝑜 + 129596581,0481′′ 0,36− 0,5532′′ 43,428 + 0,000136′′ 286,191 −0,00001149′′ 1885 = 358° 25’ 22.0” 𝐹3 ≡ 𝐹= 93,272090062𝑜 + 1739527262,8478′′ 0,36− 12,7512′′ 43,428 − 0,001037′′ 286,191 +0,00000417′′ 1885,00 = 93° 23’ 11′′ 𝐹4 ≡ 𝐷= 297,85019547𝑜 + 1602961601,2090′′ 0,36− 6,3706′′ 43,428 + 0,006593′′ 286,191 −0,00003169′′ 1885,00 = 297° 57’ 20” 𝐹5 ≡ Ω = 125,04455501𝑜 − 6962890,5431′′ 0,36+ 7,4722′′ 43,428 + 0,007702′′ 286,191 −0,00005939′′ 1885,00 = 125° 30’ 12.286” ∆𝜓= −17,21′′ sin 125° 30’ 12.286” + 0,003′′ cos 125° 30’ 12.286” −1,32′′sin 2(93° 23’ 11′′ − 297° 57’ 20”+ 125° 30’ 12.286”) − 0,23′′ sin 2(93° 23’ 11′′ + 125° 30’ 12.286”) +0,21′′ sin 2 125° 30’ 12.286” + 0,15′′ sin 358° 25’ 22.0” − 0,05′′ sin(358° 25’ 22.0” + 2 93° 23’ 11′′ − 2 297° 57’ 20” + 2 125° 30’ 12.286”) + 0,07′′ sin 135° 4’ 35” = −17,21′′ 0,814 - 0,003′′ 0,5807 +1,32′′ 0,3725 − 0,23′′ 0,9773 -0,21′′ 0,9455 - 0,15′′ 0,0275 + 0,05′′ 0,3631 + 0,07′′ 0,7062 = −14,01′′-−0,0017′′+0,4917′′−0,2248′′−0,1986′′−0,0041′′+0,0181′′+0,0494′′=−13,88′′ ∆𝜀= 9,21 ′′ cos 125° 30’ 12.286” + 0,002′′ sin 125° 30’ 12.286” + 0,57′′ cos 2 (93° 23’ 11′′ − 297° 57’ 20” + 125° 30’ 12.286”) + 0,10′′ cos 2(93° 23’ 11′′ + 125° 30’ 12.286”) −0,09′′ cos 2 125° 30’ 12.286” + 0,01′′ cos 358° 25’ 22.0” + 0,02′′ cos(358° 25’ 22.0” + 2 93° 23’ 11′′ − 2 297° 57’ 20” + 2 125° 30’ 12.286”) = = 9,21′′ (-0,5807) + 0,002′′ 0,8141 + 0,57′′ 0,9280 + 0,10′′ 0,2117 + +0,09′′ 0,3254 + 0,01′′ 0,9996 - 0,02′′ 0,9379 = =-5,348′′ +0,0016′′+0,5290′′+0,0211′′+0,0293′′+0,10′′=-4,667′′ 5. Вычисляем координаты вектора пункта i в истинной равноденственной системе координат на момент наблюдения 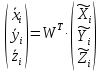 где 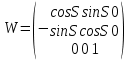 матрица суточного вращения Земли; матрица суточного вращения Земли; 𝑆= 6ℎ 41𝑚 50,54841𝑠 + 8640184,812866𝑠 𝑡+ 0,093104𝑠 𝑡2 − 6,2𝑠 10−6 𝑡3 + +𝑈Т1 + 0,06667∆𝜓cos𝜀 – момент гринвичского звёздного времени; 𝜀= 84381,448′′ − 46,84024′′ 𝑡− 0,00059′′ 𝑡2 + 0,001813′′ 𝑡3 - средний наклон эклиптики к экватору. 𝜀= 84381,448′′ − 46,84024′′ 0,36− 0,00059′′ 43,428 + 0,001813′′ 286,191 = = 84381,448′′ − 308,67718′′− 0,02562′′ + 0,051886′′ = 84072,79709′′ 𝑆= 6ℎ 41𝑚 50,54841𝑠 + 8640184,812866𝑠 0,36+ 0,093104𝑠 43,428 − 6,2𝑠 10−6 286,191 + 19ℎ 012 56,112𝑠 + 0,06667(−13,88′′) 0,9181 = 6ℎ 41𝑚 50,54841𝑠 + 56938817,91579𝑠+ 4,04332𝑠 – 0,00117𝑠 + 19ℎ 012 56,112𝑠 - 0,84959 𝑠 = = 6ℎ 41𝑚 50,54841𝑠 + 56938821,10835𝑠 + 19ℎ 012 56,112𝑠 = = 6ℎ 41𝑚 50,54841𝑠 + 158ℎ 20𝑚 21,10𝑠 + 19ℎ 012 56,112𝑠 = 184ℎ 04𝑚 08,76041𝑠 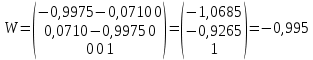  6. Вычисляем истинные топоцентрические координаты вектора спутника в равноденственной системе координат на момент наблюдения 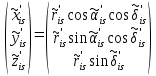 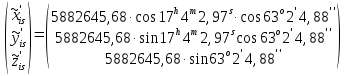 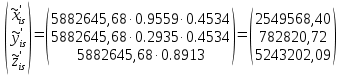 7. Вычисляем истинные геоцентрические координаты вектора спутника s в равноденственной системе координат на момент наблюдения 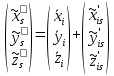 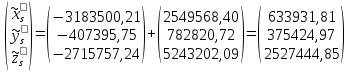 8. Вычисляем прецессионные параметры Ньюкома-Андуайе 𝜁𝐴 =2,5976176′′ + 2306,0809506′′ 𝑡+ 0,3019015′′ 𝑡2 + 0,0179663′′ 𝑡3 −0,0000327′′ 𝑡4−0,0000002′′ 𝑡5; 𝜃𝐴 = 2004,1917476′′𝑡− 0,4269353′′ 𝑡2 − 0,0418251′′ 𝑡3 − 0,0000601′′ 𝑡4 − 0,0000001′′ 𝑡5; 𝑧𝐴 = −2,5976176′′ + 2306,0803226′′ 𝑡+ 1,0947790′′ 𝑡2 + 0,0182273′′ 𝑡3 +0,0000470′′ 𝑡4 − 0,0000003′′ 𝑡5 𝜁𝐴 =2,5976176′′ + 2306,0809506′′ 0,36+ 0,3019015′′ 43,43 + 0,0179663′′ 286,19 −0,0000327′′ 1885,00−0,0000002′′ 12428,74 = 2,5976176′′ + 15197,07346′′+13,11582′′+5,14177′′−0,06164′′−0,00248′′= 15217,86455′′ 𝜃𝐴 = 2004,1917476′′ 0,36− 0,4269353′′ 43,43 − 0,0418251′′ 286,19 − 0,0000601′′ 1885,00− 0,0000001′′ 12428,74 = 13207,62363′′− 18,54157′′ − 11,96846′′ − 0,11310′′− 0,00124′′ = 13176,99926′′ 𝑧𝐴 = −2,5976176′′ + 2306,0803226′′ 0,36+ 1,0947790′′ 43,43 + 0,0182273′′ 286,19 +0,0000470′′ 1885,00 − 0,0000003′′ 12428,74 = −2,5976176′′ + 15197,06931′′+47,54629′′+5,21647′′+0,08859′′−0,00373′′ = 15247,31931′′ 9. Формируем матрицы прецессии и нутации 𝑃= 𝑅3 (−𝑧𝐴)𝑅2 (𝜃𝐴)𝑅3 (−𝜁𝐴) 𝑁= 𝑅1 (−𝜀− Δ𝜀)𝑅3 (−Δ𝜓)𝑅1 (𝜀) , где 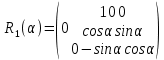 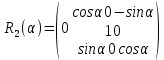 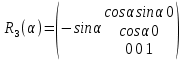 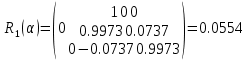  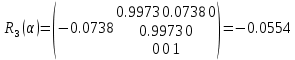 𝑃= -0.0554 (−15247,31931′′)*0.0445 (13176,99926′′)*(-0.0554) (−15217,86455′′) = -12.4946′′ 𝑁= 0.0554 (−84072,79709′′+4,667′′)*(-0.0554) *13,88′′)*0.0554 (−84072,79709′′) = - 41.9930′′ 10. Вычисляем средние геоцентрические координаты вектора спутника s в равноденственной системе координат на стандартную эпоху J2000.0 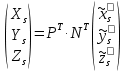 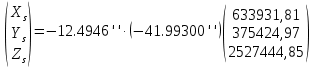 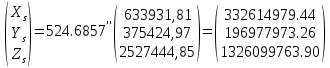 11. Вычисляем полярные средние геоцентрические координаты спутника s в равноденственной системе координат на стандартную эпоху J2000.0 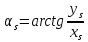 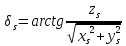 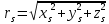  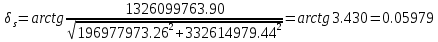  Задание № 2 Вычисление элементов невозмущённой орбиты по наблюдениям спутника с пункта земной поверхности Постановка задачи Пусть с пункта земной поверхности, координаты которого известны, выполнены наблюдения искусственного спутника Земли и определены топоцентрические направления и расстояния до трёх его мгновенных положений. В результате вычислены геоцентрические прямоугольные координаты этих мгновенных положений. Требуется вычислить элементы орбиты спутника. Для решения подобной задачи разработано много методов определения орбит. Наиболее широко используемым является классический метод Гаусса. Здесь приводится алгоритм модифицированного метода Гаусса. Исходные данные
Решение: 1. Вычисляем геоцентрические прямые восхождения, склонения и модули векторов ИСЗ для трёх его положений 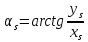 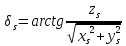 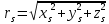 Для точки 0 с: 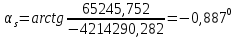 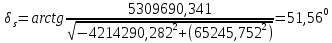 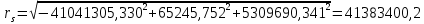 Для точки 120 с: 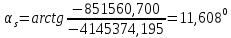  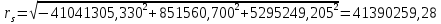 Для точки 240 с: 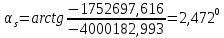 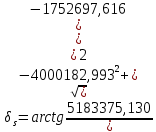 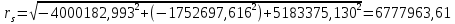 2. Вычисляем угол наклона i плоскости орбиты ИСЗ к плоскости экватора Земли по формуле 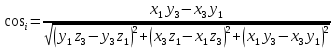 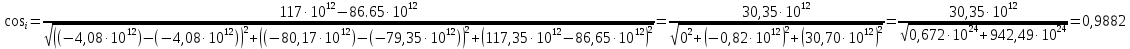 = = Угол i равен 0°59'17".520 3. Вычисляем долготу восходящего узла Ω орбиты ИСЗ, используя формулы  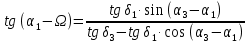 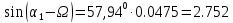 Ω = 0°11'34".800 4. Вычисляем значения аргументов широты для трёх положений ИСЗ  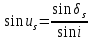 Для точки 0 с  = 0°59'51".720 = 0°59'51".720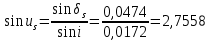 = 2°45'20".880 = 2°45'20".880Для точки 120 с 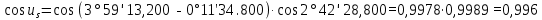 = 0°59'48".120 = 0°59'48".120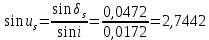 = 2°44'39".120 = 2°44'39".120Для точки 240 с 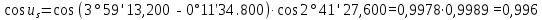 = 0°59'48".120 = 0°59'48".120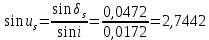 = 2°44'39".120 = 2°44'39".120Вычисляем фокальный параметр 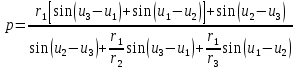 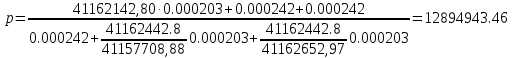 5. Вычисляем истинную аномалию для первого положения ИСЗ, используя формулы 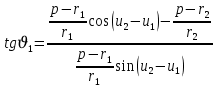 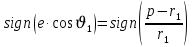 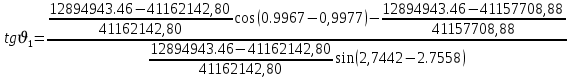 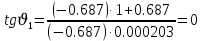 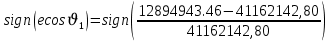 6. Вычисляем эксцентриситет орбиты 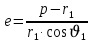 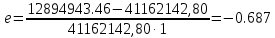 7. Вычисляем аргумент перицентра 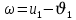 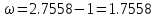 8. Вычисляем большую полуось орбиты  9. Вычисляем среднее движение 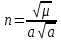 где μ = 3,9860044*1014 м3с-2 - геоцентрическая гравитационная постоянная 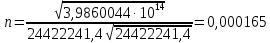 10. Вычисляем эксцентрическую аномалию ИСЗ для его первого положения по формулам 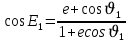 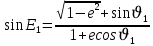  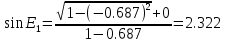 E = 0.0405 или 0°2'26" 11. Вычисляем момент предыдущего прохождения ИСЗ через перицентр   12. Вычисляем значение средней аномалии 𝑀1 на момент времени 𝑡1 𝑀1 = n(𝑡1 – 𝜏) 𝑀1 = 0.000165(0 – 5.75) = 0.000949 | |||||||||||||||||||||
