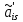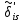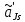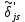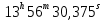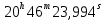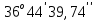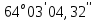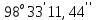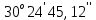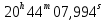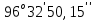Реферат по геодезии. Работа. Постановка задачи и исходные данные
 Скачать 177.21 Kb. Скачать 177.21 Kb.
|
|
Задание № 3 Вычисление невозмущённой эфемериды ИСЗ Постановка задачи и исходные данные В качестве исходных данных студент использует элементы орбиты 𝑎, 𝑒, i, Ω, 𝜔, 𝑀1 в момент времени 𝑡1 , вычисленные в задании № 2. Требуется на заданный момент времени 𝑡= 𝑡1 + 3ℎ вычислить прямоугольные координаты 𝑥, 𝑦, 𝑧 и составляющие скорости 𝑥,̇ 𝑦,̇ 𝑧 искусственного спутника Земли. Решение: 1. Вычисляем среднее движение ИСЗ 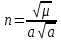 где μ = 3,9860044*1014 м3с-2 - геоцентрическая гравитационная постоянная 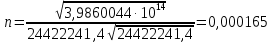 2. Вычисляем среднюю аномалию на заданный момент времени t 𝑀= 𝑀1 + n(𝑡− 𝑡1 ) 𝑀= 0.000949 + 0.000165(240− 120) = 0,0207 3. Задавшись точностью вычислений ε, методом последовательных приближений вычисляем эксцентрическую аномалию 𝐸0 = 𝑀+ 𝑒sin𝑀; 𝐸𝑘 = 𝑀+ 𝑒sin𝐸𝑘−1 , k=1,2…,n. Вычисления прекращаем, когда |𝐸𝑘 − 𝐸𝑘−1 | < 𝜀= 0,0000001𝑜 𝐸0 = 0.0207+ (-0.687)* 0.000364 = 0.02045 при k=1 𝐸𝑘 = 0,0207+ (-0.687)*sin0= 0,0207 при k=2 𝐸𝑘 = 0,0207+ (-0.687)*sin1= 0,009 и т.д. 4. Вычисляем истинную аномалию 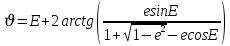 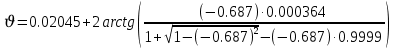 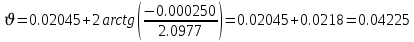 5. Вычисляем аргумент широты 𝑢= 𝜔+ 𝜗 = 1.7558+0.04225 = 1.7980 6. Вычисляем геоцентрическое расстояние до спутника 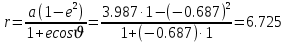 7. Вычисляем прямоугольные координаты спутника 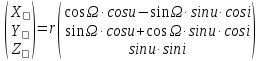 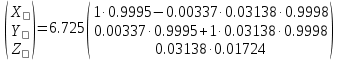 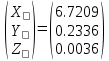 8. Вычисляем составляющие скорости спутника 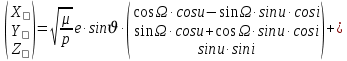 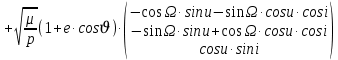 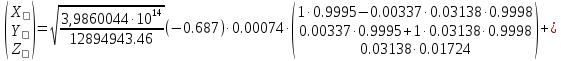 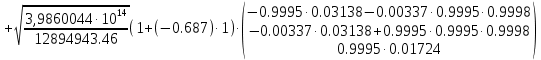  Задание № 4 Вычисление элементов орбиты ИСЗ по координатам и составляющим скорости Постановка задачи и исходные данные На момент времени t заданы координаты x, y, z и составляющие скорости 𝑥,̇ 𝑦,̇ 𝑧̇ искусственного спутника Земли. Требуется вычислить элементы орбиты a, e, i, Ω, ω, M на тот же момент времени. В качестве исходных данных студент использует результаты, полученные в задании № 3. Решение: 1. Вычисляем постоянные площадей 𝑐1 = 𝑦𝑧̇− 𝑦̇𝑧 ; 𝑐2 = 𝑥̇𝑧− 𝑥𝑧̇ ; 𝑐3 = 𝑥𝑦̇− 𝑥̇𝑦; 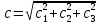 𝑐1 = 0,2336*(-0,05028)− (2,92036*0,0036) = -0,12791 𝑐2 = (-2,72615)*0,0036− 6,7209*(-0,05028)=-0,34774 𝑐3 = 6,7209*(-2,92036)− (-2,72615*0,2336) = -18,99057 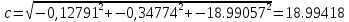 2. Вычисляем фокальный параметр 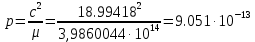 3. Вычисляем угол наклона плоскости орбиты к плоскости экватора 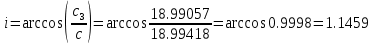 4. С помощью формул 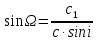 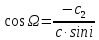 вычисляем долготу восходящего узла Ω 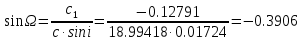 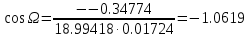 Ω = 0.00681 5. Вычисляем квадрат скорости спутника и геоцентрическое расстояние до спутника 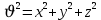 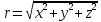 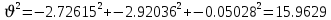 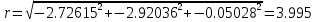 6. Вычисляем постоянную энергии 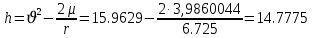 7. Вычисляем большую полуось орбиты спутника 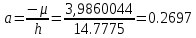 8. Вычисляем составляющие вектора Лапласа f1 =D'x− Dx' f2 =D'y− Dy' f3 =D'z− Dz' 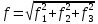 где D = x x'+ y y'+ z z' 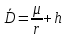 D = 6.7209 (-2.72615)+ 0.2336 (-2.92036)+ 0.0036 (-0.005028) = -19.00441 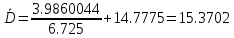 f1 =D'x− Dx'=19.00441*6.7209-15.3702*(-2.72615) = 169.6282 f2 =D'y− Dy' = 15.3702*0.2336-19.00441*(-2.92036) = 59.08929 f3 =D'z− Dz'=19.00441*0.0036-15.3702*(-0.005028)=0.14570 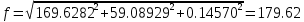 9. Вычисляем эксцентриситет орбиты спутника по формулt^ 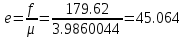 10. На основании формулы вычисляем аргумент перицентра 𝜔 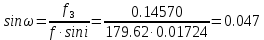 ω = 2.690 11. С помощью формулы вычисляем истинную аномалию 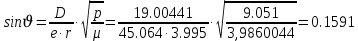 𝜗 = 9.15470 12. С помощью формулы вычисляем эксцентрическую аномалию 𝐸. 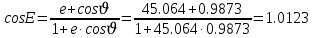 E =11.428 13. Вычисляем среднюю аномалию 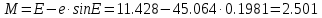 Задание № 5 Вычисление ориентирующих углов земной хорды по наблюдениям спутника с двух пунктов земной поверхности. Постановка задачи. При выполнении уравнительных вычислений по определению компонентов вектора пункт-пункт необходимо располагать их приближёнными значениями. Вычисление этих значений можно осуществить на основе элементарной фигуры. Элементарной фигурой называется построение, состоящее из необходимого числа измерений. При вычислении ориентирующих углов земной хорды по измеренным направлениям пункт-спутник, выполненным с обоих пунктов, элементарной будет фигура, состоящая из двух синхронных треугольников. В этом случае задача по определению ориентирующих углов хорды (единичного вектора пункт-пункт) сводится к троекратному вычислению векторных произведений соответствующих единичных векторов (метод Вяйсяля). Исходные данные
Решение: 1. Вычисляем момент гринвичского звёздного времени для первого наблюдения ИСЗ 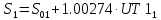 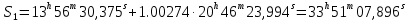 2. Вычисляем направляющие косинусы направлений пункт – спутник с обоих пунктов i и j на первый момент времени наблюдения ИСЗ 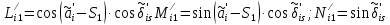 ; ; 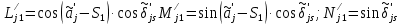 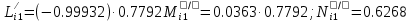 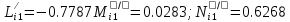 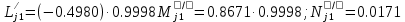 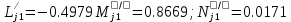 3. Вычисляем момент гринвичского звёздного времени для dnjhjuj наблюдения ИСЗ 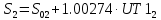 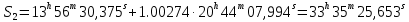 4. Вычисляем направляющие косинусы направлений пункт – спутник с обоих пунктов i и j на второй момент времени наблюдения ИСЗ 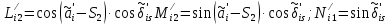 ; ; 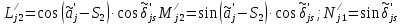 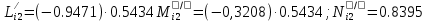 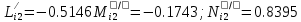 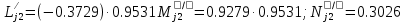 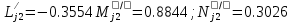 5. Вычисляем направляющие косинусы вектора, перпендикулярного синхронной плоскости, соответствующей первому моменту времени наблюдения ИСЗ 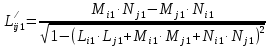 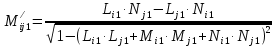 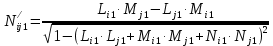 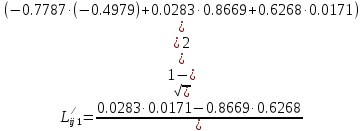 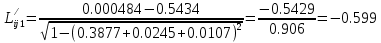 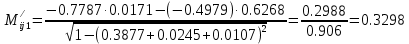 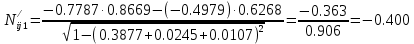 6. Вычисляем направляющие косинусы вектора, перпендикулярного синхронной плоскости, соответствующей второму моменту времени наблюдения ИСЗ 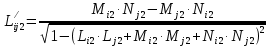 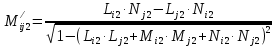 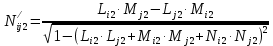 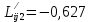 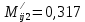 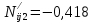 7. Вычисляем направляющие косинусы вектора пункт-пункт (земная хорда)     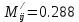 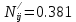 8. Вычисляем ориентирующие углы земной хорды 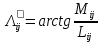 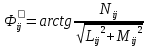 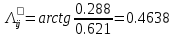 или 24°52'55" или 24°52'55"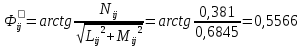 или 29°06'01" или 29°06'01"Задание № 6 Численное интегрирование системы дифференциальных уравнений возмущённого движения ИСЗ. Постановка задачи Задана система дифференциальных уравнений возмущённого движения ИСЗ вида 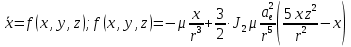 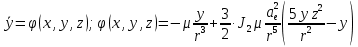 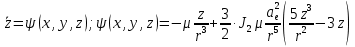 с начальными условиями интегрирования 𝑥0 , 𝑦0 , 𝑧0 , 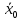 , , 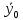 , , 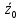 𝑡0 . 𝑡0 .Требуется вычислить координаты и составляющие скорости ИСЗ в конце первого шага H интегрирования. Шаг интегрирования принять равным 60s.
Решение: 1. Вычисляем правые части дифференциальных уравнений 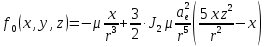 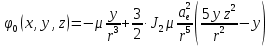 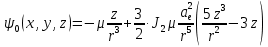 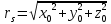 где μ = 3,9860044*1014 м3с-2 J2 = 0,001082636; ае = 6378136 м 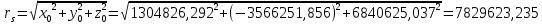 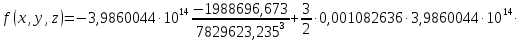 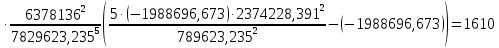 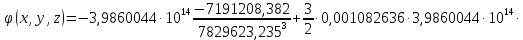 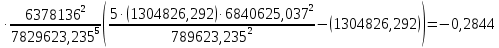 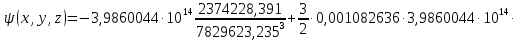 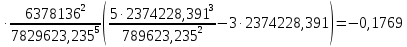 2. Вычисляем в первом приближении координаты ИСЗ в подшагах 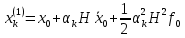 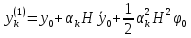 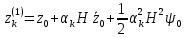 k= 1,2,3 α1 = 0,212340538 α2 = 0,590533136 α3 = 0,911412040 H=60s 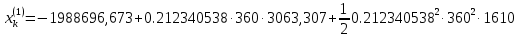 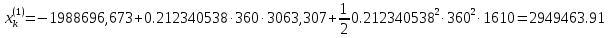 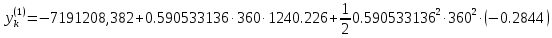 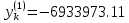 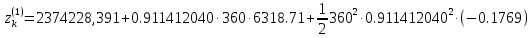 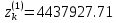 3. Вычисляем в первом приближении значения правых частей в подшагах 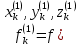 ) ) 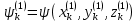 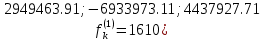 ) )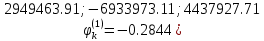 ) )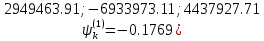 ) )4. Вычисляем в первом приближении p, q, r 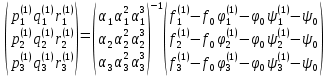 Вычисление в этом и последующем пунктах невозможны в связи с невозможностью вычисления матрицы в п.3 (неизвестны дальнейшие операции с матрицей – сложение, вычитание, умножение (?)). 5. Вычисляем во втором приближении координаты ИСЗ в подшагах 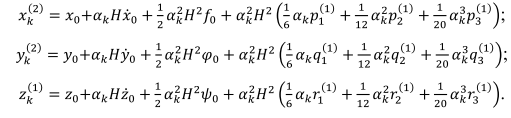 6. Вычисляем во втором приближении значения правых частей в подшагах 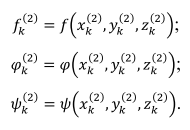 7. Вычисляем во втором приближении p, q, r 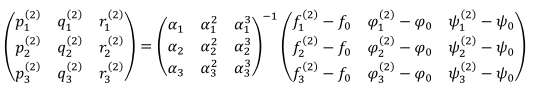 8. Процесс приближений продолжаем до тех пор, пока p, q, r не стабилизируются. После стабилизации p, q, r решение в конце шага будет 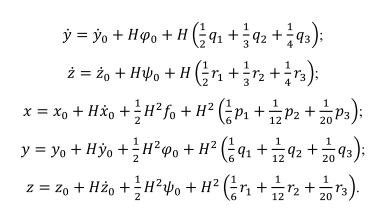 |