Векторы координаты, проекция вектора на ось, направляющие косинусы
 Скачать 128.22 Kb. Скачать 128.22 Kb.
|
|
Векторы: координаты, проекция вектора на ось, направляющие косинусы. Координаты вектора – координаты конечной точки этого вектора, если он расположен так, что его начало находится в начале координат. В противном случае, каждая координата вектора равна разности соответствующих координат его начала и конца Проекция вектора на ось – скалярная величина, равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают. Число, противоположное длине геометрической проекции вектора, если направления противоположные Направляющие косинусы – косинусы углов, которые вектор образует с положительными полуосями координат. Они однозначно задают направление вектора. 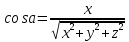 Линейные операции над векторами. Сложение векторов и умножение вектора на число А = (5; 9; 7) В = (3; -1; 6) А + В = (5+7; 9+(-1); 7+6) = (12; 8; 13) Умножение: А = (3;4;6) 2*А = (6;8;12) Скалярное произведение двух векторов и его свойства. Сумма произведений соответствующих координат векторов А = (5; 9; 7) В = (3; -1; 6) А*В = 5*3 + 9*-1 + 6*7 Произведение их длин на косинус угла между ними. Скалярное произведение двух ненулевых векторов равно 0 только тогда, когда вектора перпендикулярны. Скалярное произведение вектора на самого себя равно квадрату его длины. Поскольку косинус острого угла положителен, косинус тупого угла отрицателен, то если скалярное произведение положительно, векторы образуют острый угол, а если отрицателен – тупой угол. Векторное произведение двух векторов, его свойства. Векторным произведением двух векторов в прямоугольной системе координат трехмерного пространства называется третий вектор, такой, что Он является не нулевым, если первые два вектора коллинеарны Он перпендикулярен этим двум векторам Длина векторного произведения равна произведению длин векторов на синус угла между ними Тройка этих векторов ориентирована также как и заданная система координат 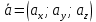 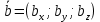 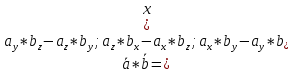 Свойства: Если определитель отрицателен, то и тройка векторов имеет ориентацию, противоположную ориентации системы координат. Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат Если определитель равен 0, то векторы компланарны (линейно зависимы) Векторное произведение в координатах представляется в виде определителя матрицы Дистрибутивность – распределительный закон. Свойство согласованности двух бинарных операций, которые определены на одном и том же свойстве. Смешанное произведение трех векторов и его свойства. Смешанным произведением трех векторов a, b, c, взятых в указанном порядке, называется скалярное произведение вектора a на векторное произведение b на c. То есть число a(b*c) или (b*c)a Различные виды уравнения прямой на плоскости. Уравнение прямой на плоскости в прямоугольной системе координат 0ху есть некоторое уравнение с двумя переменными х и у, которое обращается в тождество при подстановке в него координат любой точки этой прямой. Общий Вид: Ах + Ву + С = 0 Где А и В – некоторые действительные числа, которые одновременно не равны нулю. В противном случае, уравнение называется неполным. Уравнение задает прямую на плоскости. Ах + Ву = 0 – уравнение задает прямую, проходящую через начало координат. Ву + С = 0 – уравнение задает прямую, параллельную оси абсцисс Ох Ах + С = 0 – уравнение задает прямую, параллельную оси ординат Оу Уравнение прямой вида 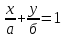 , где а и б – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках. Абсолютные величины а и б равны отрезкам, которые прямая отсекает на координатных осях Ох и Оу. , где а и б – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках. Абсолютные величины а и б равны отрезкам, которые прямая отсекает на координатных осях Ох и Оу. Для построения графика отметьте координаты (а, 0) и (0, б) и соедините их прямой линией. Уравнение вида у = кх+б, где х и у – переменные, а к и б – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом. Угол наклона прямой к положительному направлению оси абсцисс в данной прямоугольной системе координат называют угол а, который отсчитывают от положительного направления оси Ох до данной прямой против хода часовой стрелки. Если прямая параллельна оси абсцисс или совпадает с ней, то угол наклона считают равным 0 Угловой коэффициент есть тангенс угла наклона к этой прямой, то есть к = tga Если прямая параллельна оси ординат, угловой коэффициент обращается в бесконечность. Каноническое уравнение прямой на плоскости имеет вид 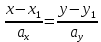 Где x1, y1, ax, и ay – некоторые действительные числа, причем ax, ay – не равны нулю. Прямая линия, определяемая этим уравнением, проходит через точку М1(х1, у1) Числа ах и ау представляют собой координаты направляющего вектора. Уравнение плоскости в пространстве. Ax+By+Cz+D=0 − общее уравнение плоскости P, где N=(A,B,C) − нормальный вектор плоскости P. 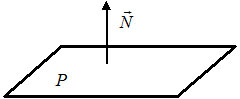 A(x - 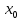 ) + B(y – ) + B(y – 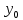 ) + C(z – ) + C(z – 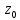 ) = 0 – уравнение плоскости P, которая проходит через точку M( ) = 0 – уравнение плоскости P, которая проходит через точку M(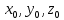 ) перпендикулярно вектору N = (A, B, C). Вектор N называется нормальным вектором плоскости. ) перпендикулярно вектору N = (A, B, C). Вектор N называется нормальным вектором плоскости. 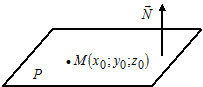 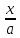 + + 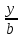 + + 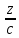 = 1 – уравнение плоскости в отрезках на осях, где a, b и с – величины отрезков, которые плоскость отсекает на осях координат. = 1 – уравнение плоскости в отрезках на осях, где a, b и с – величины отрезков, которые плоскость отсекает на осях координат. 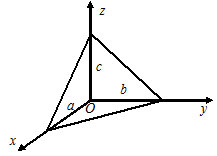 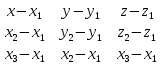 = 0 – уравнение плоскости, которая происходит через три точки A( = 0 – уравнение плоскости, которая происходит через три точки A(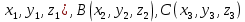 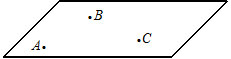 xcosa + ycosb + zcosy – p = 0 – нормальное уравнение плоскости, где cosa, cosb, cosy - направляющие косинусы нормального вектора N, направленного из начала координат в сторону плоскости, a p > 0 – расстояние от начала координат до плоскости. Взаимное расположение плоскостей в пространстве. Две пересекающиеся плоскости: две плоскости называют пересекающимися, если они не совпадают, и у них есть общие точки. В случае, когда две плоскости пересекаются, пересечением этих плоскостей является прямая линия. Две параллельные плоскости: две плоскости называют параллельными, если они не имеют общих точек. Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны. Если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то такие плоскости параллельны. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Эллипс – геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек F1, F2 (фокусы), есть величина постоянная, равная 2а. 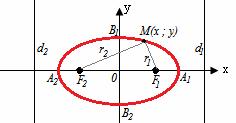 Элементы эллипса: A1A2=2a - большая ось B1B2=2b - меньшая ось A1 ,A2 , B1 ,B2 , - вершины F1(c ; 0), F2(-c ; 0) - фокусы F1F2=2c - фокальное расстояние c2=a2-b2 Эксцентриситет – мера вытянутости эллипса. Чем больше он, тем меньше отношение b к a. Каноническое уравнение: 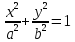 Окружность – частный случай эллипса, когда a, b, c = 0. Каноническое уравнение: x2+y2=R2 Гипербола – геометрическое место точек, для каждой из которых модуль разности расстояний от нее до двух данных точек F1, F2 (фокусы) есть величина постоянная равная 2а. 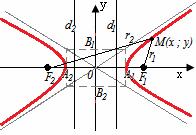 Элементы гиперболы: A1A2=2a - действительная ось B1B2=2b - мнимая ось A1 ,A2 - вершины F1(c ; 0), F2(-c ; 0) - фокусы F1F2=2c - фокальное расстояние (фокусное расстояние) c2=a2+b2 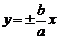 - асимптоты - асимптоты Парабола – геометрическое место точек, каждая из которых равноудалена от данной точки (фокус) и от данной прямой (директриса). 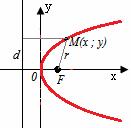 Элементы параболы 0F - фокальная ось 0 - вершина 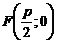 - фокус - фокус ε=1 - эксцентриситет 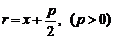 - фокальный радиус - фокальный радиус 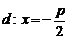 - директриса - директриса p - фокальный параметр Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы): y2=2px При p<0 ветви параболы направлены влево. Если фокальная ось совпадает с осью Oy, то уравнение параболы имеет вид: x2=2py При p>0 ветви параболы направлены вверх, при p<0 -вниз. Общий вид уравнения кривой второго порядка. Общий вид уравнения кривой второго порядка называется уравнение: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 Коэффициенты А, В, С одновременно не равны нулю. Линии, определяемые такими уравнениями, называются кривыми второго порядка. Центром некоторой линии называется точка плоскости, по отношению к которой, точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными. Координаты центра S(x0 ; y0) линии определяются из системы: 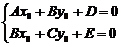 Матрицы, операции над матрицами. Две матрицы называют равными, если они имеют одинаковые размеры и их соответствующие элементы равны. Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число. Суммой матриц А и В одного размера называется матрица С, получаемся из исходных путем сложения соответствующих элементов. Произведением матрицы Am×n на матрицу Bn×kназывается матрица Cm×k такая, что элемент матрицы C, стоящий в i-ой строке и j-ом столбце, т.е. элемент Cij, равен сумме произведений элементов i-ой строки матрицы Aна соответствующие элементы j-ого столбца матрицы B. Транспонирование матрицы – операция, над матрицей, когда ее строки становятся столбцами с теми же номерами. Элементарные преобразования строк матрицы. Элементарные преобразования над строками матрицами называются следующие преобразования строк: умножение строки на ненулевое число; перестановка двух строк; прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число. Если от матрицы А к матрице В перешли с помощью эквивалентных преобразований над строками, то такие матрицы называют эквивалентными. Приведение матрицы к ступенчатому виду и виду Гаусса. 1. В первом столбце выбрать элемент, отличный от нуля (ведущий элемент). Строку с ведущим элементом (ведущая строка), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые. 2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить. 3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа). 4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы. Ранг матрицы. Ранг матрицы – наивысший порядок определителя, отличного от нуля. Ранг – положительное число. Для нулевой матрицы – ранг равен нулю. 15.Определитель квадратной матрицы, его свойства. Методы вычисления определителей. Определителем матрицы первого порядка называется число, равное единственному элементу этой матрицы. Квадратная матрица называется вырожденной, если ее определитель равен нулю. И невырожденной если определитель отличен от нуля. Определитель транспонированной матрицы равен определителю исходной. Умножение всех элементов строки или столбца определителя на некоторое число равносильно умножению определителя на это число Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю. Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали Если все элементы k-ой строки (столбца) определителя представлены в виде сумм ak j + bk j, то определитель можно представить в виде суммы соответствующих определителей Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей Для вычисления определителя второго порядка, нужно из произведения элементов главной диагонали отнять произведение побочной диагонали Правило треугольника (третьего порядка) 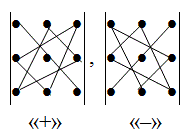 Разложение определителя по строке или столбцу. Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой. С помощью элементарных преобразований над строками или столбцами определитель приводится к ступенчатому виду и тогда его значение, согласно свойствам определителя, равно произведению элементов, стоящих на главной диагонали. Обратная матрица: свойства, способы построения. Матрица называется А1 обратной, если произведение исходной матрицы и А1 равно Е, где Е – единичная матрица n-ого порядка. Обратная матрица может существовать только для квадратных матриц.
(A·B)-1 = A-1·B-1 (A-1)T = (AT)-1
(A-1)-1 = A Если определитель не равен нулю, обратная матрица существует. В противном случае – нет. Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной. При этом, если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной. Матрица А1, элементы которой равны алгебраическим дополнения соответствующих элементов матрицы А называется союзной матрицей. Совместность и определенность системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Критерий совместности системы линейных алгебраических уравнений. Система совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу расширенной матрицы, при этом система имеет единственное решение, если ранг равен числу неизвестных. Бесконечное множество, когда ранг меньше числа неизвестных. Теорема применяется при исследованиях систем алгебраических уравнений без непосредственного решения системы. В результате исследования должна быть записана эквивалентная система уравнений с минимальным числом уравнений. Решение систем линейных алгебраических уравнений с помощью правила Крамера. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается знаком дельта Определители дельта(х1) и дельта(х2) получают путем замены коэффициента при соответствующих неизвестных свободными членами: 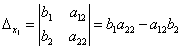 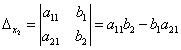 теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка. Формула Крамера для нахождения неизвестных: 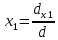 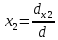 Решение систем линейных алгебраических уравнений методом Гаусса. Линейная зависимость и независимость векторов. Линейная однородная система алгебраических уравнений, ее фундаментальная система решений. Связь решений линейных однородных и неоднородных систем. Решение систем линейных алгебраических уравнений с помощью обратной матрицы. 23.Комплексные числа, алгебраическая форма записи комплексных чисел, основные действия с комплексными числами. 24.Геометрическое представление комплексного числа. Тригонометрическая форма записи комплексного числа. Переход от алгебраической формы записи комплексного числа и обратно. Показательная форма записи комплексного числа. Формула Эйлера. Рассмотрим комплексное число, которое записано в тригонометрической форме: 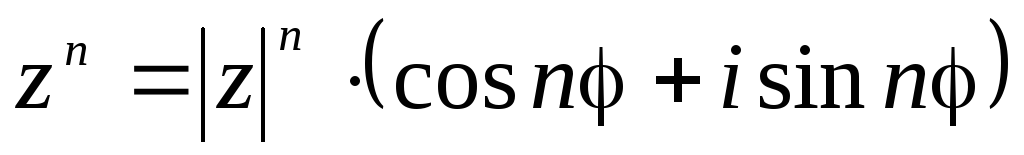 По формуле эйлера: 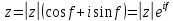 Следовательно, любое комплексное число можно представить в так называемой показательной форме: 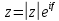 Действия умножения и деления комплексных чисел в тригонометрической и показательной формах записи. Действие извлечение корня для комплексных чисел. Если комплексное число z задано в тригонометрической форме 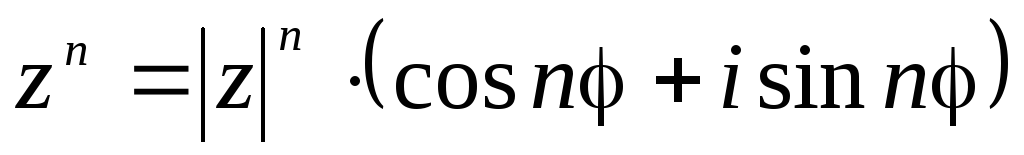 то все значения корня n-ой степени вычисляются по формуле Муавра: Многочлены. Основная теорема алгебры. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный. Если многочлены p(z), q(z), степени которых не превосходят n, имеют равные значения более, чем при n различных значения переменной z, то эти многочлены равны p(z) = q(z). Если комплексное, но не действительное число с – корень многочлена p(c) с действительными коэффициентами, то сопряженное число с1 является его корнем той же кратности. Многочлен нечетной степени с действительными коэффициентами всегда имеет хотя бы один действительный корень. Собственные значения, собственные векторы матрицы. Характеристическое уравнение матрицы. Свойства собственных значений матрицы. |
