МПЗ. Мпз модель представления знаний
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
МПЗ Модель представления знаний – это способ записи знаний, предназначенный для отображения текущего состояния объектов некоторой предметной области и отношений между ними, а также изменение объектов и отношений. Модель представления знаний может быть универсальной, то есть применимой для большинства предметных областей, или специализированной, то есть разработанной для конкретной предметной области. К основным универсальным моделям представления знаний относятся: - логические модели; - сетевые модели; - продукционные модели; - фреймовые модели. Знания хранятся в базе знаний в соответствии с моделью представления знаний. Логические модели В основе логических моделей лежит понятие формальной теории, задаваемой четверкой: S = < T, F, A, R >. Рассмотрим компоненты формальной теории. T – множество символов теории S, называемых термами и образующих алфавит теории. Конечная последовательность символов множества T называется выражением теории S. F – подмножество выражений теории S, называемых формулами теории и построенных по синтаксическим правилам. Примерами правил могут быть праивла записи формул алгебры высказываний. A – множество формул, называемых аксиомами теории S и являющихся априорно истинными формулами. R – конечное множество отношений между формулами, называемые правилами вывода. Правила вывода позволяют получать новые формулы множества F за счет применения этих правил вывода к аксиомам или уже выведенным формулам. Формальная система позволяет выводить новые правильные формулы множества F, применяя к аксиомам множества A и уже полученным формулам правила вывода множества R, то есть выводить из одних истинных высказываний новые истинные высказывания. Таким образом, в рамках формальной системы можно получить бесконечное число формул из небольшого числа исходных аксиом. Вывод новых знаний в рамках логической модели представления знаний заключается в получении некоторого утверждения из имеющихся аксиом и правил вывод. Если в результате вывода утверждение получено, то оно считается истинным и является логическим следствием из аксиом. В этом случае задачей пользователя или программиста является описание предметной области совокупностью утверждений в виде логических формул. Доказательство истинности утверждения осуществляется ЭВМ на основе исходных утверждений. Семантические сети Семантическая сеть – это система знаний, имеющая вид сети, узлы которой соответствуют объектам предметной области и их свойствам, а дуги – отношениям между ними. Семантическая сеть представляет собой ориентированный граф с поименованными дугами и вершинами. Вершинам графа, описывающего семантическую сеть, соответствуют: - события представляют собой действия, происходящие в реальном мире; - объекты представляют объекты реального мира, а также их особенности и характеристики (цвет, размер, качество), а применительно к событиям – продолжительность, время, место. Дуги графа семантической сети отображают многообразие отношений между объектами, которые условно можно разделить на четыре класса: - лингвистические отношения в свою очередь подразделяются на глагольные (время, вид, род, залог, наклонение), атрибутивные (цвет, размер, форма) и падежные; - логические отношения, используемые в алгебре высказываний: дизъюнкция, конъюнкция, отрицание, импликация и др.; - теоретико-множественные: отношение части целого (PART-OF), отношение множества и элемента (IS-A); - квантифицированные отношения общности и существования; они используются для представления таких утверждений как «Любой станок надо ремонтировать», «Существует работник А, обслуживающий склад Б». Выделим основные события в этом предложении, соответствующие действиям: F1 – студент пришел; F2 – пришел, чтобы сдать. Схема семантической сети представлена на рис. 7.2. 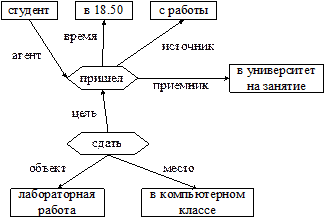 Рис. 7.2. Представление знаний семантической сетью Продукционная модель Эта модель называется продукционной, так как все знания представляются в виде продукций – правил вида ЕСЛИ A, ТО B, 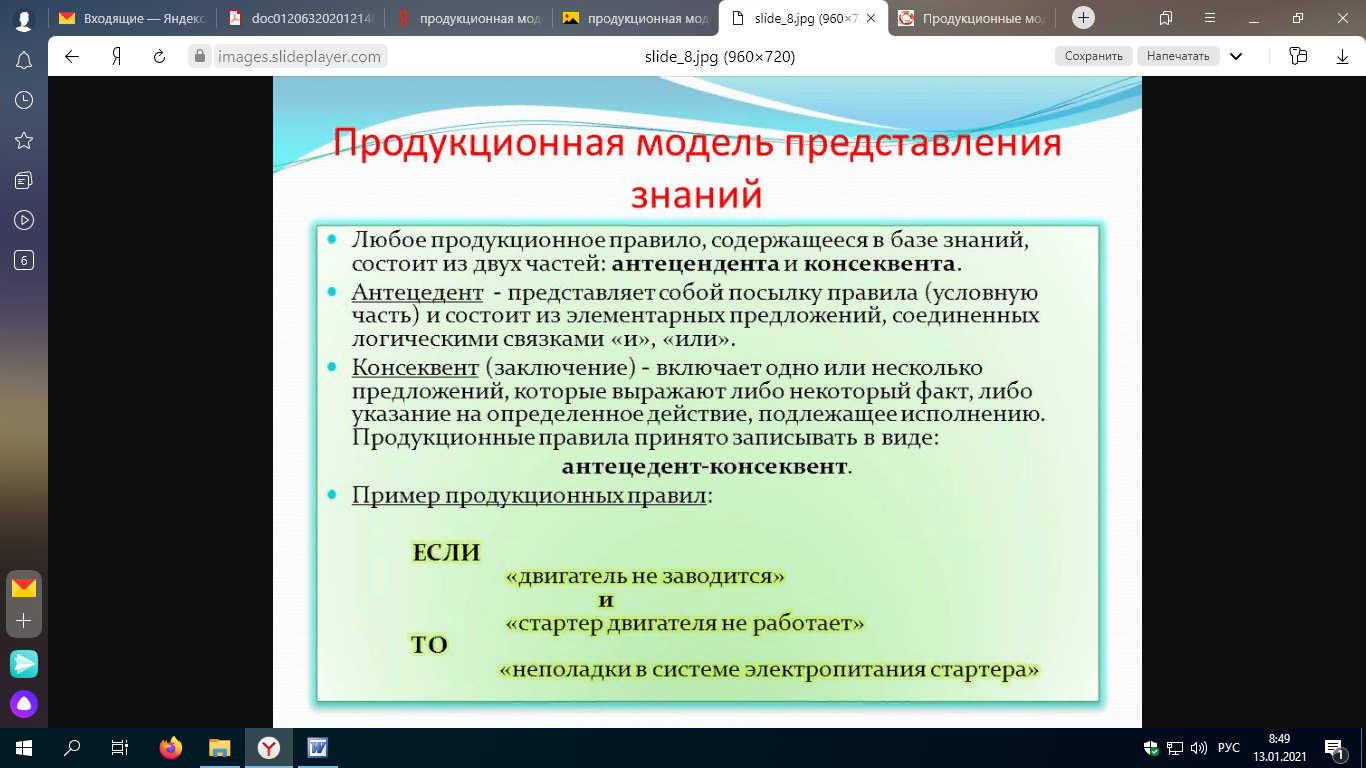 Условная часть состоит из одного или нескольких высказываний, соединенных операциями конъюнкции. Заключение состоит из одного высказывания. Если высказывания условной части истинны, то высказывание заключительной части тоже считается истинным. Правила, условная часть которых истинна на некотором этапе логического вывода, образуют фронт готовых продукций. Математические или программные средства, обрабатывающие знания, представленные правилами, называются продукционными системами или системами продукций. Популярность продукционных моделей определяется следующими факторами: - простой и точный механизм использования знаний: подавляющая часть человеческих знаний может быть записана в виде продукций; - однородность: знания описываются по единому синтаксису; - параллельность: одновременно могут обрабатываться несколько правил. При большом числе продукций (более 1000) продукционная модель имеет, по крайней мере, два недостатка: - усложняется проверка непротиворечивости продукций; - усложняется проверка правильности работы логического вывода. Системы продукций состоят из двух частей: 1) БЗ, состоящая из правил; 2) блок логического вывода новых знаний из правил БЗ. Прямой логический вывод и обратный логический вывод Фрейм – это структура данных, представляющая стереотипную ситуацию, вроде нахождения внутри некоторого рода жилой комнаты, или сбора на вечеринку по поводу дня рождения ребенка. К каждому фрейму присоединяется несколько видов информации. Часть этой информации – о том, как использовать фрейм. Часть о том, чего можно ожидать далее. Часть о том, что следует делать, если эти ожидания не подтвердятся. Фрейм представляет собой множество слотов. Каждый слот представляется определённой структурой данных – атрибутами слота. Структура фрейма приведена на рисунке 1.
Основная идея фреймового подхода заключается в сосредоточении всей информации, относящейся к одному объекту в одной структуре данных, вместо распределения ее по базе знаний. Структура фрейма достаточно проста (рисунок 2): с представляемым понятием связывается список именованных атрибутов, называемых слотами. Каждый слот может иметь значение по умолчанию. 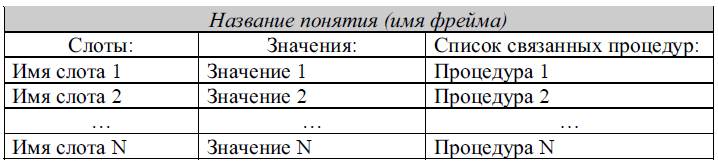 Пример.Фрейм для понятия "Лекция". Ситуация "лекция" может быть определена как "чтение лектором учебного материала слушателям". Фрейм "лекция" может содержать слоты "предмет" (предмет, по которому проводится лекция), "лектор" (ФИО лектора), "аудитория" (место проведения лекции), "слушатели" (количество слушателей).
В данном случае "ЛЕКЦИЯ" - название фрейма; "ПРЕДМЕТ", "ЛЕКТОР", "АУДИТОРИЯ", "СЛУШАТЕЛИ - слоты; " Базы знаний ", "Иванов И.И.", "1-13 к 13 ", " Прикладная-информатика 1курс " - значения слотов. Фрейм-прототип (протофрейм) - это фрейм, содержащий знания о самом понятии. Фрейм-экземпляр (экзофрейм) - это фрейм, содержащий конкретное описание понятия или знания. Исключение из фрейма любого слота делает его принципиально не полным, а иногда вообще бессмысленным. Фрейм является простым, если он не содержит в себе других фреймов. Сложный (составной) фрейм содержит в себе два и более фрейма, и по существу представляет сеть фреймов. Фрейм позволяет отобразить все многообразие знаний о мире через: - фреймы – структуры, использующиеся для обозначения объектов и понятий (заем, залог, вексель); - фреймы – роли (менеджер, кассир, клиент); - фреймы – сценарии (банкротство, собрание акционеров, празднование именин); - фреймы – ситуации (тревога, авария, рабочий режим устройства) и др. | |||||||||||||||||
