гидравлика и аэродинамика (pdf.io). Муромский институт
 Скачать 4.92 Mb.
|
|
3. Вихрь Рассмотрим комплексный потенциал w= Alnz. Пусть А- действительное число z=re , w= +i , = Alnr, = A . Линии тока лучи =const.Изопотенциальные линии - окружности. Найдём расход Q=Imvdz=Im dzdz=Im zdz=Im 2iA)=2A, resf(z)= 2i f(zdz=(a)=lim(z−a)f(z), A= 2 , w= 2 lnz - комплексный потенциал источника или стока мощности Q( рис. 60 ). Пусть А- чисто мнимое равное Вi, где В - действительное. w= Bilnz Источник Вихрь y A=Re y A=Im x x а б Рис. 4 МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 17  = Re Bidz= ReBi2i = −2B, B= − , w(z)= − ilnz= lnz - вихрь. МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 18  4. ВихреисточникРассмотрим случай комплексного коэффициента при логарифме w(z)= (A+Bi)lnz. y x Рис. 5 Такойкомплексныйпотенциал можнорассматриватькак результат наложения двух потоков w(z)= Alnz, w2(z)= Bilnz, w(z)= Q−ilnz - комплексный потенциал вихреисточника( рис. 5 ). МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 19  5. Диполь Рассмотрим комплексный потенциалw= z, 1 x−iyx yx+iyx2 +y2 x2 +y2 x2 +y2 , = x2 +y2 , =− x2 +y2 . Найдём семейство линий тока =const, =c=−x2 +y2 , x2 + y2 = −cy x2 +y−22 = 22. Линии тока - окружности с центрами на оси oy. y x Рис. 6 Изопотенциальные линии - окружности с центрами на оси ox( рис. 62 ).Диполь w= m , где m- момент диполя МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 20 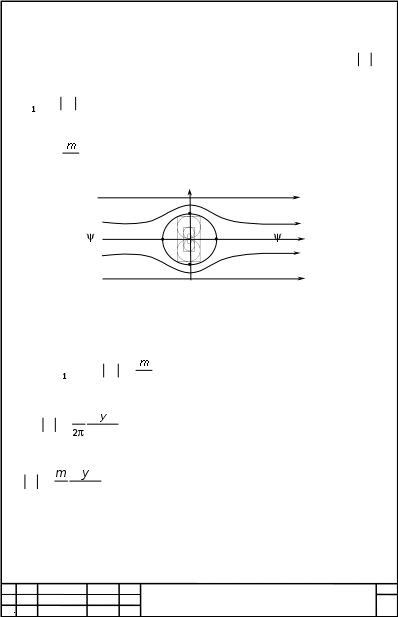 6. Бесциркуляционное обтекание цилиндраНаложим плоский параллельный оси oxоднородный поток со скоростью v и комплексным потенциалом ( рис. 63 ) w(z)= v z на скоростное поле диполя с комплексным потенциалом w2(z)= 2z, yC =0 A B =0 x D Рис. 7 w(z)= w+w2 = v z+ 2z. Для определения функции тока отделим мнимую часть = v y− mx2+y2 =const. Нулевая линия тока v y−2 x2+y2 =0 представляет собой две кривые : 1) окружность МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 21 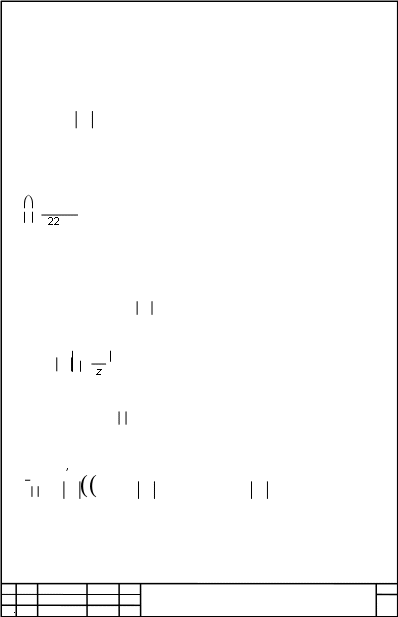 x2 + y2 = m, 2) ось oxy= 0. Выберем произвольную до сих пор величину момента диполя равной m=2a2 v . Получим нулевую линию тока в виде совокупности окружности радиуса а с центром в начале координат и оси ox. Остальные линии тока 1− a2 y=const x+y . Движение происходит в двух областях - вне и внутри круга. Течение вне круга можем рассматривать как обтекание круглого цилиндра, с радиусом основания равным а плоскопараллельным потоком, имеющим на бесконечности скорость v . Такому потоку соответствует комплексный потенциал w(z)= v z+a2 , z a Остановимся подробнее на внешнем течении. Найдём распределение скоростей в области z a. Найдём распределение скоростей на поверхности цилиндра z=aei vz=a= v 1−e−2i )= v e−i ei −e−i )=2iv e−i sin . Определим модуль скорости на контуре круга МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 22 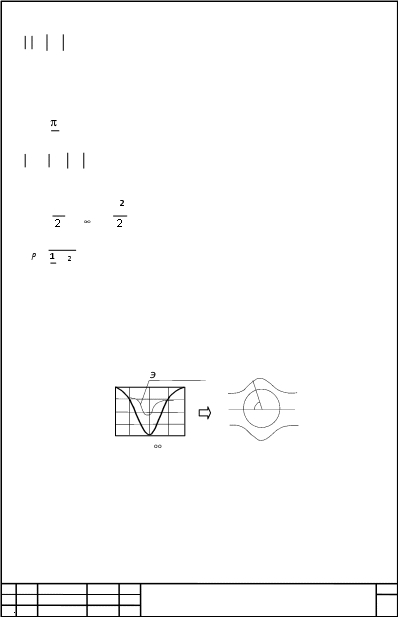 v=2v sin .Отсюда следует, что при плоском безвихревом обтекании кругового цилиндра идеальной жидкостью скорость распределена по закону синуса. Максимальная скорость при = 2 vmax = 2v . Используя уравнение Бернулли, можно найти распределение давления p+ v2 = p+ v , C= p−p =1−4sin2 2v , где Cp- коэффициентдавления. На рис. 64 показано распределение коэффициента давления по поверхности цилиндра. ксперимент 1 0 A B-1 -2 -3 0 90 180 а б Рис. 8 МИВУ.080316.001 КР Изм Лист № докум. Подп. Дата Лист 23  |