Дневник_отчет_Погосян_3. Национальный исследовательский ядерный университет мифи институт финансовых технологий и экономической безопасности кафедра финансовый мониторинг
 Скачать 1 Mb. Скачать 1 Mb.
|
Глава II2.1 Принципы работы с большими даннымиОсновные принципы с большими данными: Горизонтальная масштабируемость. Данные могут быть сколько угодно много. Любая система, которая подразумевает обработку данных, должна быть расширяемой. Отказоустойчивость. Принцип масштабируемости подразумевает, что машин в кластере может быть много. Например, Hadoop кластер Yahoo имеет более 4200 машин. Локальность. В больших распределенных системах данные распределены по большему количеству машин. Если данные находятся на одном сервере, а обкатывается в другом сервере, то расходы могут не окупаться. По этой причине, следует большим данным обрабатывать данных на той машине, на которой хранится. Все средства для больших данные в современном мире, следует этим принципам. Чтобы им следовать-они должны придумывать свойственные методы, способы и парадигмы для разработки данных. Техники и методы анализа, применяемые к большим данным:  Степень использования данных в разных отраслях на примере:
2.2 Построение модели с фиктивными переменнымиО линейных регрессионных моделях с переменной структурой будем говорить в тех случаях, когда на результативную переменную помимо отобранных и измеренных объясняющих признаков оказывают существенное воздействие некоторые меняющиеся (одновременно с предопределёнными переменными во времени и/или в пространстве) качественные факторы, что может вести к скачкообразным изменениям коэффициентов линейной регрессии. Очевидна идея, связанная с 3разбиением исходных статистических данных на качественно-однородные группы и последующей оценкой функции регрессии в каждой из таких групп. Но такой подход либо ведёт к снижению статистической надёжности результатов, либо невозможен ввиду малого объёма выборки хотя бы в одной из регрессионно-однородных подвыборок. Выход заключается во введении фиктивных переменных («манекенов»), однако следует обоснованно подходить к их введению, поскольку каждая новая переменная ведёт к уменьшению степеней свободы и снижению надёжности выводов. Приобретение навыков построения и анализа эконометрических моделей по регрессионно-неоднородным данным является целью предлагаемой работы. По имеющимся данным о рынке жилья в Коврове, продемонстрируем процедуру построения регрессионной модели по неоднородным данным: Y1 –стоимость однокомнатной квартиры (тыс. руб.); Y2 –стоимость двухкомнатной квартиры (тыс. руб.); Х1- дом улучшенной планировки, дом хрущёвка; X2 – расположение квартиры (промежуточный этаж, первый/последний этаж); X3-дом панельный (блочный)/кирпичный; X4-жилая площадь, (кв.м); X5- общая площадь (кв.м); 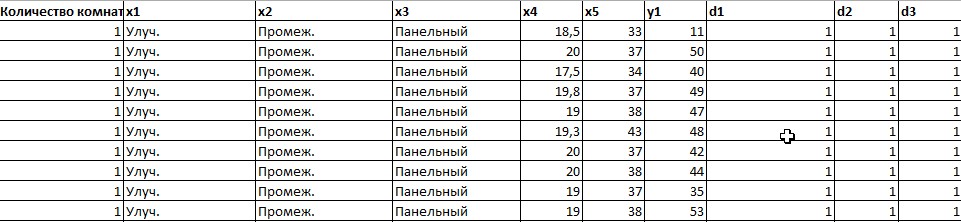 Рисунок 1-исходные данные По имеющимся данным о рынке строящегося жилья в г. Коврове, продемонстрируем процедуру построения регрессионной модели по неоднородным данным. В нашем случае результативные признаки: Y1 - Стоимость однокомнатной квартиры (тыс.руб) Y2 - Стоимость двухкомнатной квартиры (тыс.руб) Объясняющие признаки: 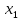 - Дом улучшенной планировки или «хрущевка»; - Дом улучшенной планировки или «хрущевка»;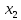 - Квартира, расположенная на одном из промежуточных, первых (последних) этажей; - Квартира, расположенная на одном из промежуточных, первых (последних) этажей;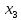 - Дом панельный/кирпичный; - Дом панельный/кирпичный;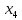 - Жилая площадь, кв.м; - Жилая площадь, кв.м;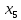 - Общая площадь, кв.м. - Общая площадь, кв.м.Построим модель множественной регрессии для Y1 и Y2 Таблица 1 – Результаты множественной регрессии для Y1
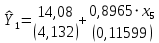 Таблица 2 – Результаты множественной регрессии для Y2
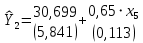 Таблица 3 –Результаты множественной регрессии для объединенной выборки
Далее устраняем мультиколлинерность с помощью метода пошаговой регрессии. 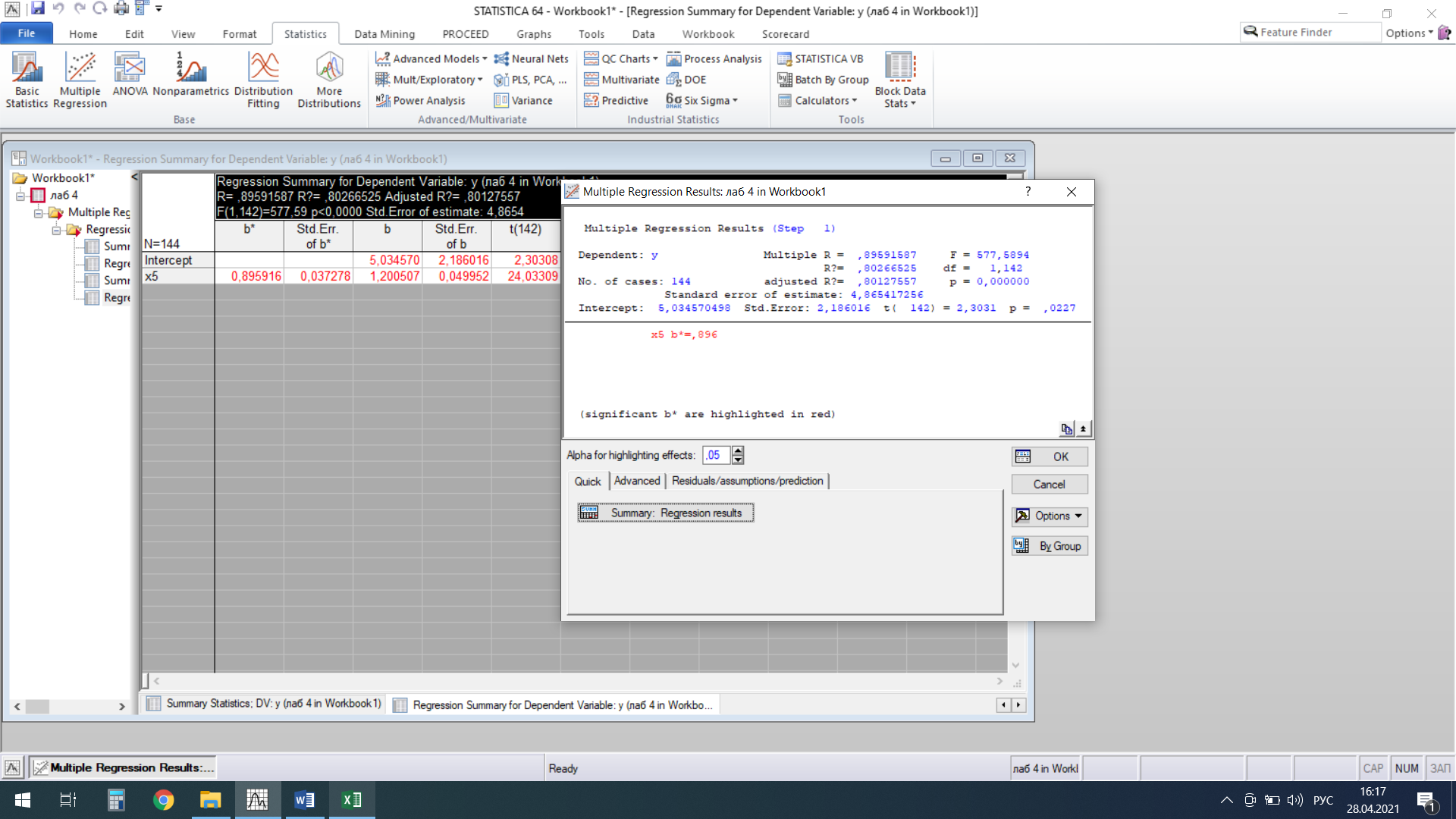 Рисунок 1- Результаты множественной регрессии для объединенной выборки после устранения мультиколлинеарности
Табл. 4 – Результаты множественной регрессии для объединенной выборки после устранения мультиколлинеарности 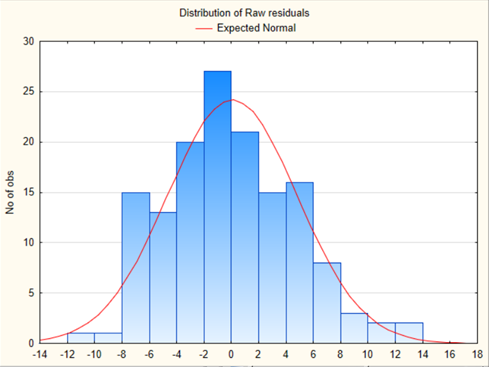 Рис.2 - Гистограмма регрессионных остатков Поскольку можно предположить нормальный характер распределения регрессионных остатков (рис.2) На основании отчета делаем выводы: - модель значима; - значимое влияние на результативные признаки-1 комнатные и 2 комнатные квартиры, оказывает объясняющая переменная – общая площадь квартиры; -Оценка уравнения регрессии: 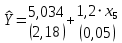 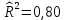 Введем фиктивные перемены На цену квартиры могут влиять качественные переменные х1-дом улучшенной планировки/дом хрущёвка, х2-квартира расположена на одном из промежуточных этажей/квартира расположена на первом (последнем) этаже, х3- дом панельный/дом кирпичный, х6- квартира однакомнатная/двухкомнатная. Проверим эти гипотезы. Так как качественные признаки ( 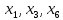 ) имеют две градации, то для них введем фиктивные переменные. Качественный признак ( ) имеют две градации, то для них введем фиктивные переменные. Качественный признак (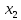 ) имеет три градации, то для него введем следующие фиктивные переменные: ) имеет три градации, то для него введем следующие фиктивные переменные: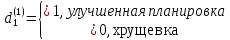 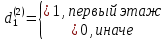 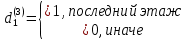 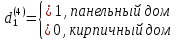 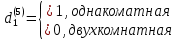 Таким образом, модель регрессии будем искать в виде: 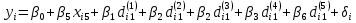 Но прежде, чем вводить фиктивные переменные необходимо проверить выборочную совокупность на регрессионную однородность, применяя критерий Чоу. Разделим всю совокупность на две подвыборки. Так как объем подвыборок достаточно велик, то проверим гипотезы об однородности выборочных совокупностей: 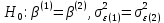 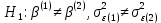 Гипотеза проверяется с помощью этой статистики: 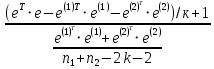 В условиях справедливости H0 эта статистика распределена по закону Фишера – Снедекора с 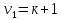 и и 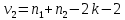 . .Построив уравнение по объединенной выборке, получили следующие результаты: Табл. 5 – Результаты оценивания параметров регрессионной модели
Табл. 6 – Результаты дисперсионного анализа
Находим значение суммы квадратов остатков 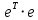 = 3326,92. = 3326,92.Аналогично оцениваем регрессионные остатки для каждой под выборки. Для фиктивной переменной 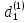 : :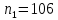 «улучшенная планировка» «улучшенная планировка»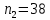 «хрущевка» «хрущевка»Для квартир с улучшенной планировкой (n1=106), получим следующие результаты: Табл. 7 – Результаты дисперсионного анализа для 106 объектов
Для квартир хрущевок (n2=38), получим следующие результаты: Табл. 8 – Результаты дисперсионного анализа для 38 объектов
Таким образом, 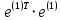 = 1947,75 = 1947,75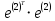 = 720,655 = 720,655Подставим полученные результаты в формулу. 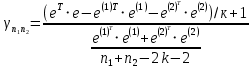 = = 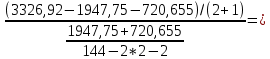 11,35 11,35На уровне значимости 0,05 и числу степеней свободы 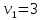 и и 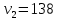 , найдем , найдем 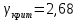 по таблице Фишера-Снедекора. по таблице Фишера-Снедекора. Так как 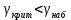 , то гипотеза Н , то гипотеза Н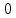 отвергается, следовательно, подвыборки неоднородны. отвергается, следовательно, подвыборки неоднородны. Для фиктивной переменной 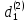 : :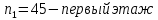 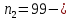 иначе иначеДля квартир, находящихся на первом этаже (n1=45), получим следующие результаты: Табл. 9 – Результаты дисперсионного анализа для 45 объектов
Для квартир, находящихся на остальных этажах (n2=99), получим следующие результаты: Табл. 10 – Результаты дисперсионного анализа для 99 объектов
Таким образом, 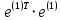 = 836,423 = 836,423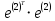 = 1922,14 = 1922,14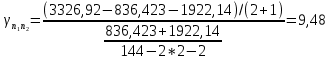 На уровне значимости 0,05 и числу степеней свободы 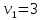 и и 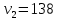 , найдем , найдем 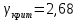 по таблице Фишера-Снедекора. по таблице Фишера-Снедекора.Так как 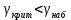 , то гипотеза Н , то гипотеза Н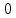 отвергается, следовательно, подвыборки неоднородны. отвергается, следовательно, подвыборки неоднородны.Для фиктивной переменной 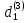 : :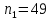 – последний этаж – последний этаж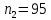 - иначе - иначеДля квартир, находящихся на промежуточном этаже (n1=49), получим следующие результаты: Табл. 11 – Результаты дисперсионного анализа для 49 объектов
Для квартир, находящихся на первом (последнем) этаже (n2=95), получим следующие результаты: Табл. 12 – Результаты дисперсионного анализа для 49 объектов
Таким образом, 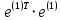 = 1066,423 = 1066,423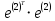 = 1784,89 = 1784,89 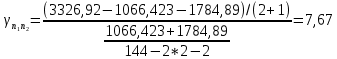 На уровне значимости 0,05 и числу степеней свободы 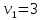 и и 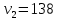 , найдем , найдем 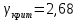 по таблице Фишера-Снедекора. по таблице Фишера-Снедекора.Так как 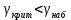 , то гипотеза Н , то гипотеза Н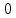 отвергается, следовательно, подвыборки неоднородны. отвергается, следовательно, подвыборки неоднородны. Для фиктивной переменной 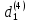 : :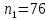 «панельный дом» «панельный дом»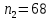 «кирпичный дом» «кирпичный дом»Для квартир в панельном доме (n1=76), получим следующие результаты: Табл. 13 – Результаты дисперсионного анализа для 76 объектов
Для квартир в кирпичном доме (n2=68), получим следующие результаты: Табл. 14 – Результаты дисперсионного анализа для 68 объектов
Таким образом, 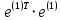 =1037,346 =1037,346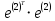 =1578,928 =1578,928 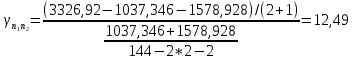 На уровне значимости 0,05 и числу степеней свободы 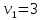 и и 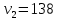 найдем найдем 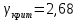 по таблице Фишера-Снедекора. по таблице Фишера-Снедекора.Так как 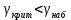 , то гипотеза Н0 отвергается, следовательно, подвыборки неоднородны. , то гипотеза Н0 отвергается, следовательно, подвыборки неоднородны. Для фиктивной переменной 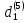 : :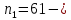 однокомнатная квартира однокомнатная квартира Для квартир в панельном доме (n1=61), получим следующие результаты: Табл. 15 – Результаты дисперсионного анализа для 61 объектов
Для квартир в кирпичном доме (n2=83), получим следующие результаты: Табл. 16 – Результаты дисперсионного анализа для 83 объектов
Таким образом, 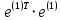 = 936,374 = 936,374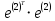 = 1396,095 = 1396,095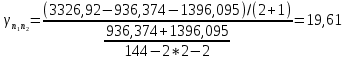 На уровне значимости 0,05 и числу степеней свободы 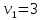 и и 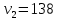 найдем найдем 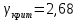 по таблице Фишера-Снедекора. Так как по таблице Фишера-Снедекора. Так как 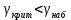 , то гипотеза Н0 отвергается, следовательно, подвыборки неоднородны. , то гипотеза Н0 отвергается, следовательно, подвыборки неоднородны.В системе Statistica для удобной работы с переменными, принимающими текстовые значения, реализован так называемый механизм "двойной записи". Согласно этому, каждому текстовому значению переменной ставится в соответствие некоторое число. Таким образом, устанавливается соответствие вида Число=Текстовое значение. Построим уравнение множественной регрессии результативной переменной Y с использованием количественных переменных 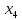 , , 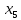 , и качественных переменных , и качественных переменных 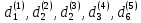 и затем устраним мультиколлинеарность методом пошаговой регрессии. и затем устраним мультиколлинеарность методом пошаговой регрессии.Табл. 17 - Результаты множественной регрессии
Табл. 18 – Результаты множественной регрессии после устранения мультиколлинеарности
На уровне значимости 0,05 можно принять нулевую гипотезу о том, что распределение регрессионных остатков не отличаются от нормального. 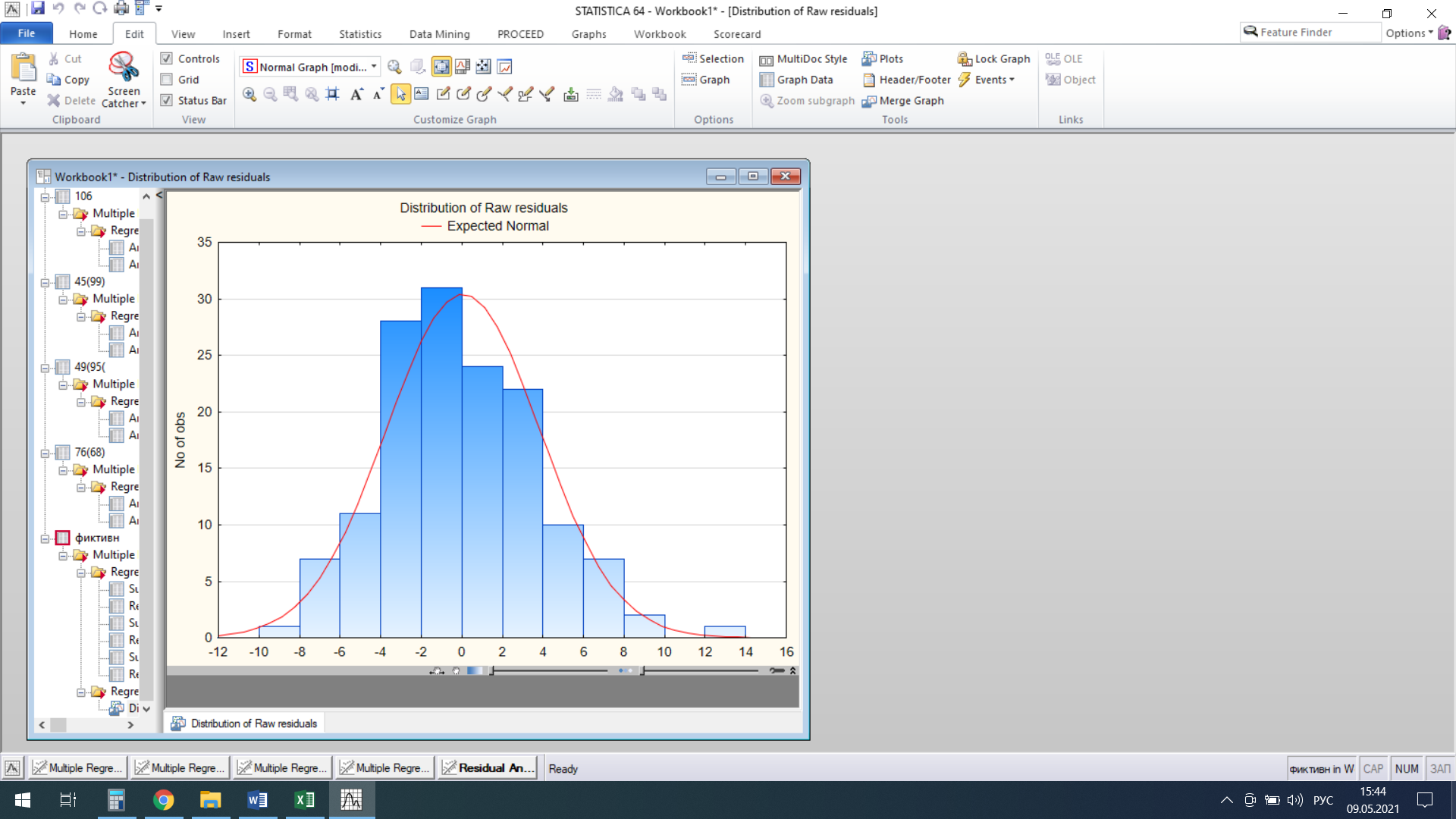 Рис. 4 – Гистограмма регрессионных остатков | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
