ЛР 3 Терехова (1). Национальный Исследовательский Ядерный

• Название: Национальный Исследовательский Ядерный
• Дата: 03.05.2022
• Размер: 67.79 Kb.
• Имя файла: ЛР 3 Терехова (1).docx
• Тип: Отчет; #508952

Национальный Исследовательский Ядерный

Университет МИФИ

Институт атомной энергетики

Институт Интеллектуальных кибернетических систем

Отчёт

по лабораторной работе №3 по Моделированию систем

“ Вычисление интегралов методом Монте-Карло”

Студент: Терехова А. Н.

Группа: ИС-Б19

Проверила: Гулина О. М.


Обнинск. 2022

Постановка задачи:

вычислить приближённо данный интеграл, используя метод Монте-Карло, двумя способами. Сравнить полученные значения интеграла, выборочной дисперсии.
Вариант 4
Вычисление интеграла:



1 метод). Метод Монте-Карло с постоянной плотностью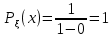


- плотность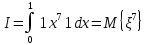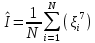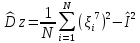











- выборочная дисперсия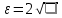


– ошибка
2 метод). Метод Монте-Карло с функцией плотности распределения (метод существенной выборки)

Нужно найти коэффициент k, используя условие нормировки: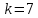






После постановки k в заданную плотность распределения, находим величину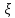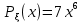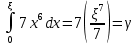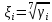

.







Введем эту плотность под наш интеграл и вычислим его с помощью метода Монте-Карло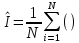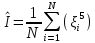








- выборочная дисперсия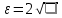


- ошибка

Код и алгоритм программы:
1)Вычисляем интеграл методом Монте-Карло с постоянной плотностью

(1 способ)
void FirstWay()

{

cout<<"ПЕРВЫЙ СПОСОБ"<
for(int j =0;j

Mx1+=pow(mass[j],7)/N;

Dx1+=pow(Mx1,2)/N;

}
Dx1=Mx1-pow(Mx1,2);

Epsilon1=2*sqrt(Dx1/N);

cout<<"Мат. ожидание при "<

cout<<"Дисперсия при "<

cout<<"Ошибка "<

}

2) Вычисляем интеграл методом Монте-Карло с заданной функцией плотности (2 способ)
void SecondWay()

{

cout<<"ВТОРОЙ СПОСОБ"<
for(int s =0;s

NewMass[s]=pow(mass[s],1.0/7);

Mx2+=NewMass[s]/7;

Dx2+=pow(NewMass[s],2);
}

Mx2=Mx2/N;

Dx2=Dx2/(49*N)-pow(Mx2,2);

Epsilon2=2*sqrt(Dx2/N);

cout<<"Мат. ожидание при "<

cout<<"Дисперсия при "<

cout<<"Ошибка "<

}
3)Полученные результаты











Сравнительные таблицы и графики

N	1 способ	2 способ
100	Mx=0.123986 Dx=0.0626438 ε =0.0500575	Mx=0.124528 Dx=0.000198732 ε =0.00281945
500	Mx=0.104667 Dx=0.0473164 ε =0.0194559	Mx=0.123701 Dx=0.000255657 ε = 0.00143013
1000	Mx=0.10824 Dx=0.0965241 ε =0.0196493	Mx=0.124441 Dx=0.000235998 ε =0.000971593
1500	Mx=0.112866 Dx=0.100127 ε =0.0163403	Mx= 0.12421 Dx=0.000260914 ε =0.000834129
2000	Mx=0.116523 Dx= 0.102946 ε =0.0143489	Mx=0.124267 Dx=0.000262706 ε =0.000724853
10000	Mx= 0.124555 Dx= 0.0507928 ε = 0.00450745	Mx= 0.124762 Dx= 0.00025753 ε = 0.000320955

Ваш генератор проверен для 10000?
Графики зависимости значения интеграла от количества случайных величин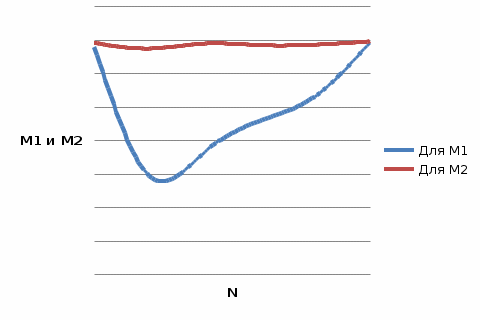


Графики зависимости дисперсии от количества случайных величин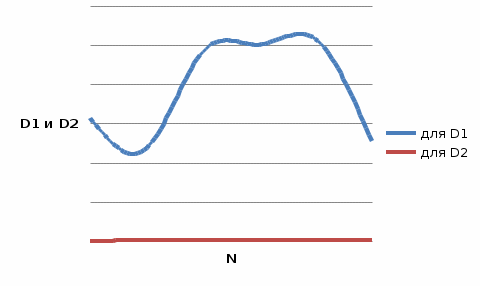

Графики зависимости погрешности эпсилон от количества случайных величин

Вывод:

В ходе выполнения работы были получены значения данного интеграла с помощью метода Монте-Карло, при разных плотностях и количестве случайных величин.

Полученные значение близки к точному значению интеграла:



Это неправда!!!

Замечено, что при увеличении количества используемых случайных величин уменьшается погрешность вычисления интеграла. Также второй метод дает наиболее точное значение интеграла (на 0.1 % точнее, чем первый).
При количестве случайных величин, равном 10000, значение дисперсии меньше в 169 раз, а ошибки меньше в 15 раз.

Таким образом, второй метод позволяет вычислить интеграл точнее.