цифровые измерительные приборы. Национальный технический университет украины киевский политехнический институт кафедра систем автоматизированного проектирования

• Название: Национальный технический университет украины киевский политехнический институт кафедра систем автоматизированного проектирования
• Анкор: цифровые измерительные приборы
• Дата: 04.05.2023
• Размер: 0.83 Mb.
• Имя файла: KursWork_ARC_Filter.doc
• Тип: Курсовая; #1107391
• страница: 2 из 5

Фильтр нижних частот

Вариант	FC,Гц	Аф,дБ	f1,Гц	Вф,дБ	Аппроксимация
1	500	2	800	30	по Баттерворту

3. Нормирование характеристик и электрических величин

Порядок величин, характеризующих параметры элементов электрических цепей, колеблется от 10^-12 Ф (для емкостей) до 10⁶...10⁷ Ом (для сопротивлений). Рабочие частоты колеблются в диапазоне от нескольких до миллионов герц. Таким образом, числовые значения электрических величин могут оказаться неудобными для практического использования. С другой стороны, свойства различных функций к операции синтеза не зависят от абсолютной величины коэффициентов этих функций. Поэтому целесообразно отделить рассмотрение свойств функций и техники синтеза (проектирования) от конкретных значений коэффициентов. Это достигается нормированием величин.

Вычисления можно упростить, если все функции сопротивления разделять на некоторую величину R₀, что эквивалентно изменению параметров пассивных элементов R, L и C следующим образом:

R'_н= , L'_н= , C'_н=CR₀.

Этот процесс называется изменением уровня (нормированием) сопротивлений. При таком преобразовании передаточные функции цепи, представляющие собой отношения напряжений или токов, не изменяются. При проектировании фильтров величину R₀ можно выбирать произвольно (обычно в пределах 1...100 к0м).

Для того чтобы сделать расчеты универсальными и упростить вычисления, используют также и нормирование частоты путем деления текущей частоты f на частоту f₀. В качестве нормирующей частоты f₀ в фильтрах нижних частот выбирают частоту среза f_c. Осуществив нормирование, решают задачу аппроксимации и реализации в нормированной частоте. При таком преобразовании частоты сопротивления R'_н не изменяются, индуктивное сопротивление уменьшается, а емкостное сопротивление увеличивается в ₀ раз (₀=2f₀).

4.Аппроксимация нормированной передаточной функции фильтра нижних частот
В соответствии с заданием на курсовую работу для аппроксимации амплитудно-частотной характеристики проектируемого фильтра нижних частот должна использоваться максимально плоская аппроксимация амплитудно-частотной характеристики (аппроксимация Баттерворта)
В случае ФНЧ нормирующей частотой является частота среза, т.е. f₀=f_c. При аппроксимации нормированной АЧХ по Баттерворту передаточная функция представляется и виде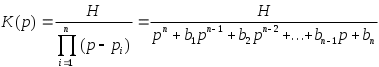

(1)

Здесь P_i - полюсы передаточной функции,



Аппроксимация по Баттерворту дает хорошее приближение АЧХ в точке F=0 (рис.2,а). По мере удаления от нее погрешность аппроксимации возрастает и достигает максимального значения на границе полосы пропускания (F=1). Нормированную частоту F₁, определяющую начало полосы задерживания, находят следующим образом:

F₁=f₁/f_c.

В полосе задерживания модуль передаточной функции фильтра Баттерворта также монотонно уменьшается.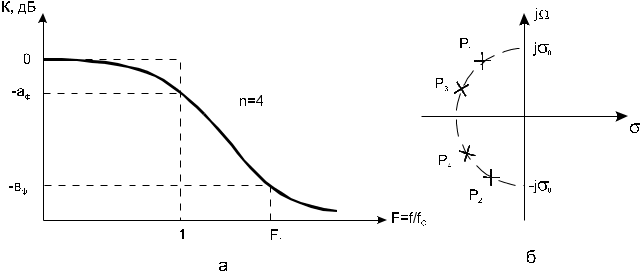


Риc.2. Аппроксимация АЧХ по Баттерворту
Порядок n аппроксимирующей функции (1) определяется по формуле

(2)

Полюсы передаточной функции располагаются и левой комплексной полуплоскости на полуокружности симметрично относительно действительной оси (рис.2,б). Их координаты рассчитываются с помощью выражения

i= , (3)

где _0–радиус полуокружности,

(4)

5. Каскадная реализация фильтра по передаточной функции K(p)
Реализация передаточных функций, обеспечивающих необходимую АЧХ , чаще всего осуществляется по методу каскадно-развязанного включения звеньев 1-го и 2-го порядков. При такой реализации передаточная функция должна быть представлена в виде произведения сомножителей 1-го и 2-го порядка K_i(p):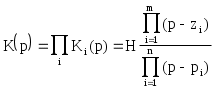

(5)


Рис.3. Каскадное соединение звеньев
Каждый из сомножителей K_i в выражении (5) реализуется соответствующим звеном. Если звенья не влияют друг на друга. то схема обладает требуемой передаточной функцией n-го порядка.

Передаточную функцию K(p) можно разложить на сомножители, используя различные комбинации постоянных множителей H_i, нулей и полюсов. Вещественные полюса образуют звенья 1-го порядка с передаточной функцией

, (6)

где B(p)–полином первой степени или единица;–постоянное число.

Комплексно-сопряженные полюсы образуют звенья 2-го порядка с передаточной функцией

, (7)

где В(р)–полином второй или меньшей степени;

и - постоянные коэффициенты.
Для фильтра нижних частот полином В(р) представляет собой единицу.

Для четного порядка n>2 каскадная схема содержит n/2 звеньев второго порядка, каждое с передаточной функцией типа (7). Если по­рядок n>2 является нечетным, то схема содержит (n-1)/2 звеньев второго порядка с передаточными функциями типа (7) и одно звено пер­вого, порядка с передаточной функцией типа (6).

Для звеньев второго порядка, описываемых функцией (7), опре­делим:

собственную частоту

(8)

и добротность

(9)

Для обеспечения коэффициента передачи фильтра в полосе пропускания равного единице (0 дБ) необходимо соблюдать условие

(10)

Так как операционные усилители обладают большим входным и малым выходным сопротивлениями, то звенья, построенные с их применением, практически не влияют друг на друга.

Реализация передаточных функций первого порядка

для фильтров нижних частот

Для фильтров нижних частот нечетного порядка одно звено должно обладать передаточной функцией первого порядка.

Звено ФНЧ первого порядка должно реализовывать передаточную функцию вида:

(11)

Для реализации звена первого порядка можно использовать инвертирующий усилитель. На рис.4 изображена схема звена ФНЧ первого порядка с инвертирующим операционным усилителем. Передаточная функция такого звена имеет вид

(12)

Сопоставляя формулы (11) и (12), получаем расчетные соотношения (при выбранном нормированном значении емкости С)





Рис.4. Звено ФНЧ первого порядка с инвертирующим ОУ

Реализация передаточных функций второго порядка

для фильтров нижних частот

Для звена фильтра нижних частот второго порядка типовая передаточная функция имеет вид

(13)

На рис.5 изображено звено второго порядка, собранное по схеме с многопетлевой обратной связью (МОС). Эта схема реализует передаточную функцию с инвертирующим коэффициентом усиления (К<0) и параметрами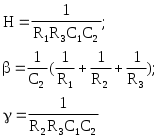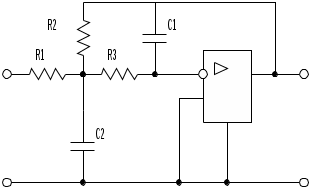





Рис.5. Звено ФНЧ второго порядка с МОС
Выбрав значения С₁ и С₂ можно рассчитать сопротивления: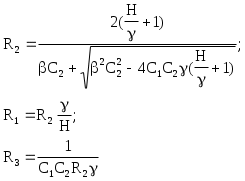


Значения емкостей С₁ и С₂ должны быть нормированными и в результате расчета давать положительное значение сопротивления R₂. Это условие выполняется, если



Схему с МОС целесообразно применять при добротностях, не превышающих 10.

При реализации звеньев второго порядка с добротностями выше 10 нужно применять более сложные схемы, например, так называемую биквадратную схему (рис.6). Такая схема реализует значения добротности вплоть до 100. Биквадратное звено ФНЧ реализует передаточную функцию (13) при неинвертирующем коэффициенте усиления и параметрах

H=1/R₁R₄C₁²; =1/R₂C₁; =1/R₃R₄C₁².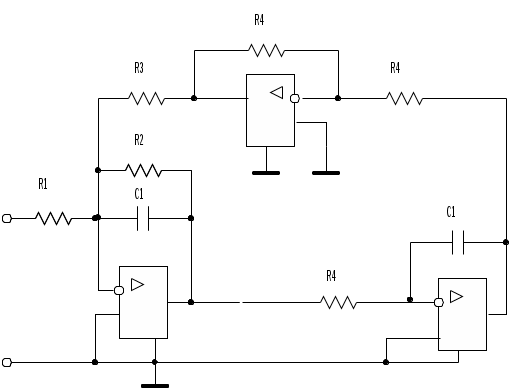



Рис.6. Биквадратное звено ФНЧ второго порядка
Значения сопротивлений определяются из следующих соотношений:

R₁=1/HC₁²R₄; R₂=1/C₁; R₃=1/R₄C₁²,

где С₁ и R₄ выбираются. Если значение С₁ выбрано близким к 10, то приемлемое значение R₄=1/C₁.

Тогда получаем: R₁=R₄/H; R₂=R₄/; R₃=R₄/.

6. Денормирование электрических величин
После реализации передаточной функции с помощью звеньев первого и второго порядка для получения реальных значений сопротивлений входящих в эти звенья компонентов необходимо параметры R и L умножить, а С - разделить на R₀.

Для перехода от нормированной циклической частоты к требуемому частотному диапазону, необходимо нормированные величины L_н и C_н разделить на ₀, т.е.

L’_H = L_H /₀

C’_H = C_H /₀ ( 14 )

R’_н = R_н.

Теперь нужно денормировать значения сопротивлений

L = L’_H R₀

C= C’_H / R₀ ( 15 )

R= R’_нR₀.
Таким образом, если нормирующими коэффициентами являются R₀ и f₀, а R_н, L_н и С_н представляют собой нормированные значения параметров пассивных компонентов, полученных в результате синтеза цепи, то их действительные значения после восстановления уровня (денормирования) сопротивлений и частоты на основании выражений (1) и (2) составят:

R=R_HR₀; C=C_H/(R₀ 2f₀ ); L=L_HR₀/(2f₀); ( 16 )
При денормировании значений параметров компонентов величину R₀ следует выбирать таким образом, чтобы значения R, C и L, рассчитанные с помощью формул (3), в рабочей области частот удовлетворяли условиям: R_вх>>R>>R_вых; R_вх>> >>R_вых; R_вх>>L>>R_вых, где R_вх, R_вых - соответственно входные и выходные сопротивления используемых активных усилительных элементов (например, операционных усилителей).

7. Расчет ненормированной АЧХ фильтра
Согласно выражению (5) передаточная функция фильтра есть произведение передаточных функций его звеньев (при условии отсутствия их взаимного влияния друг на друга)



Таким образом, передаточная функция представлена в виде произведения сомножителей 1-го и 2-го порядка K_i(p), каждый из которых реализуется соответствующим звеном.

Звено первого порядка имеет передаточную фунцию вида



Для звена первого порядка, реализованного по схеме с инвертирующим ОУ,

H=1/R₁C;

=1/R₂C;

Звено второго порядка имеет передаточную фунцию вида

,

где параметры H,, определяются исходя из номиналов компонентов, входящих в конкретное звено.

Для звена второго порядка, реализованного по схеме с многопетлевой обратной связью (МОС)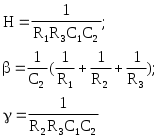



Для звена второго порядка, реализованного по биквадратной схеме:

H=1/R₁R₄C₁²; =1/R₂C₁; =1/R₃R₄C₁².
Таким образом, определив передаточную каждого звена и перемножив эти функции, получим передаточную функцию фильтра.

Осуществив подстановку

p = j 2f

и взяв модуль комплексной передаточной функции K(p), получим ненормированную АЧХ фильтра :