13задания баз уровень решение. Наглядная стереометрия

Название	Наглядная стереометрия
Дата	14.06.2022
Размер	161.69 Kb.
Формат файла
Имя файла	13задания баз уровень решение.docx
Тип	Задача #590890

Задание №13 ЕГЭ по математике базового уровня

Наглядная стереометрия

В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры – например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии – они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.

Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня

Вариант 13МБ1

Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.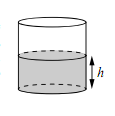

Алгоритм выполнения:

Записать формулу объема цилиндра.
Подставить значения для цилиндра с жидкостью в первом и во втором случае.
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
Полученное уравнение решить относительно второй высоты h₂.
Подставить данные и вычислить искомую величину.

Решение:

Запишем формулу объема цилиндра.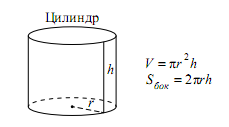

Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r².

Следовательно, объем цилиндра равен π • r² • h

Подставим значения для цилиндра с жидкостью в первом и во втором случае. V₁= π r₁² h₁ V₂= π r₂² h₂ Объем жидкости не изменялся, следовательно, можно приравнять объемы.

V₁= V₂

Левые части равны, значит можно приравнять и правые.

π r₁² h₁= π r₂² h₂

Полученное уравнение решим относительно второй высоты h₂.

h₂ – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

h₂=( π r₁² h₁)/ π r₂²

По условию площадь основания стала в 4 раза больше, то есть r₂ = 4 r₁ . Подставим r₂ = 4 r₁в выражение для h_1. Получим: h₂=( π r₁² h₁)/ π (4 r₁) ² Полученную дробь сократим на π, получим h₂=( r₁² h₁)/ 16 r₁² Полученную дробь сократим на r₁, получим h₂= h₁/ 16. Подставим известные данные: h₂= 80/ 16 = 5 см. Ответ: 5.

Вариант 13МБ2

Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?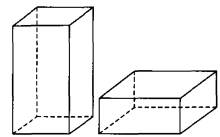

Алгоритм выполнения:

Записать формулу, для вычисления объема правильной четырехугольной призмы.
Записать в общем виде формулу для нахождения объема в первом и втором случае.
Найти отношение объемов.
Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
Сократить получившуюся дробь.

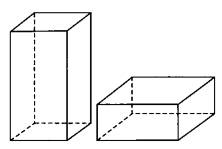Алгоритм выполнения:

Записать формулу, для вычисления объема правильной четырехугольной призмы.
Записать в общем виде формулу для нахождения объема в первом и втором случае.
Найти отношение объемов.
Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
Сократить получившуюся дробь.

Решение:

Запишем формулу, для вычисления объема правильной четырехугольной призмы.

V = a · b · c

Запишем в общем виде формулу для нахождения объема в первом и втором случае.

V₁= a₁ · b₁ · c₁

V₂= a₂ · b₂ · c₂

Найдем отношение объемов.

V₁/ V₂= (a₁ · b₁ · c₁)/ ( a₂ · b₂ · c₂)

Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.

По условию c₁ = 1,5 c₂(первая коробка в полтора раза выше второй), b₂ = 3 b₁ (вторая коробка втрое шире первой).

Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a₂ = 3 a₁

Подставим эти выражения в формулу отношения объемов:

V₁/ V₂= (a₁ · b₁ · c₁)/ ( a₂ · b₂ · c₂) = (a₁ · b₁ · 1,5c₂)/ ( 3a₁ · 3b₁ · c₂) = (a₁ · b₁ · 1,5c₂)/ ( 9a₁ · b₁ · c₂)

Сократим получившуюся дробь на a₁ · b₁ · c₂. Получим:

V₁/ V₂= (a₁ · b₁ · 1,5c₂)/ ( 9a₁ · b₁ · c₂) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.

Объем первой коробочки в 6 раза меньше объема второй. Ответ: 6.

Вариант 13МБ4

От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?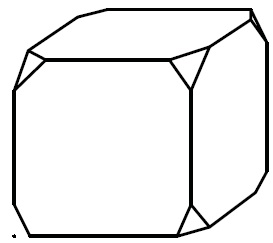

Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.

Ответ: 14.

Если бы нас спросили, а сколько вершин у нового “куба”. Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24

Вариант 13МБ5

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?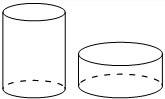

Алгоритм выполнения

Записываем ф-лу для вычисления объема цилиндра.
Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
Формируем формулы для объема 1-го и 2-го цилиндров.
Вычисляем отношение объемов.

Решение:

Объем цилиндра равен: V=πR²H. Обозначим радиус основания 1-го цилиндра через R₁, а его высоту – через Н₁. Соответственно, радиус основания 2-го цилиндра обозначим через R₂, а высоту – через Н₂. Отсюда получим: V₁=πR₁²H₁, V₂=πR₂²H₂. Запишем искомое отношение объемов: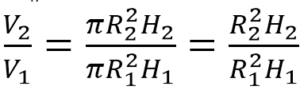

.

Подставляем в полученное отношение числовые данные: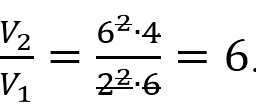

.

Вывод: объем 2-го цилиндра больше объема 1-го в 6 раз.

Вариант 13МБ6

В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

Алгоритм выполнения

Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V₁ и V₂.
Фиксируем значение для V₁. Выражаем V₂ через V₁. Находим значение V₂.
Переводим результат, полученный в литрах, в куб.см.

Решение:

Объем бака до погружения V₁=5 (л). Т.к. после погружения детали объем стал равным V₂. Согласно условию, увеличение составило 1,4 раза, поэтому V₂=1,4V₁. Отсюда получаем: V₂=1,4·5=7 (л). Т.о., разница объемов, которая и составляет объем детали, равна:

V₂–V₁=7–5=2 (л).

2 л=2·1000=2000 (куб.см).

Вариант 13МБ7

Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.

Алгоритм выполнения

Записываем ф-лу для расчета объема цилиндра.
На основании этой формулы записываем 2 уравнения – для вычисления объема воды в 1-м и 2-м сосудах. Для этого используем в формуле соответствующие индексы 1 и 2.
Поскольку воду просто переливают их одного сосуда в другой, то ее объем не изменяется. Поэтому приравниваем полученные уравнения. Из полученного единственного уравнения находим уровень воды во 2-м сосуде, выраженный высотой h₂.

Решение:

Объем цилиндра равен: V=S_оснh=πR²h. Объем воды в 1-м сосуде: V₁=πR₁²h₁. Объем во 2-м сосуде: V₂=πR₂²h₂. Приравниваем V₁ и V₂: πR₁²h₁=πR₂²h₂. Сокращаем на π, выражаем h₂: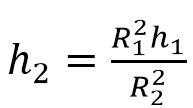

.

По условию R₂=2R₁. Отсюда:

.

Вариант 13МБ8

От деревянной правильной треугольной призмы отпилили все ее вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые ребра на рисунке не изображены)?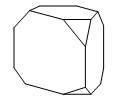

Алгоритм выполнения

Определяем количество вершин у треугольной призмы.
Анализируем изменения, которые произойдут при отпиливании всех вершин. Подсчитываем кол-во вершин у нового многогранника.

Решение:

Вершины призмы формируют вершины оснований (верхнего и нижнего). Поскольку основаниями правильной треугольной призмы являются правильные треугольники, то вершин у такой призмы 3·2=6 штук.

Спилив вершины призмы, получим вместо них небольшие (по сравнению с размерами самой призмы) треугольники. Это отображено и на рисунке. То есть вместо каждой вершины образуется 3 новых. Следовательно, их кол-во станет равным: 6·3=18.

Вариант 13МБ9

Даны две коробки, имеющие форму правильной четырехугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая второе уже первой. Во сколько раз объем первой коробки больше объема второй?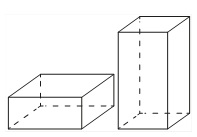

Алгоритм выполнения

Вводим обозначения для линейных параметров коробок и их объемов.
Определяем зависимость линейных параметров согласно условию.
Записываем формулу для вычисления объема призмы.
Адаптируем эту формулу для объемов коробок.
Находим отношение объемов.

Решение:

Т.к. форма коробок – правильная призма, то в их основании лежат квадраты. Поэтому можем обозначить длину и ширину каждой коробки одинаково. Пусть для первой коробки это а₁, а для второй а₂. Высоты коробок обозначим соответственно h₁ и h₂. Объемы – V₁ и V₂.

Согласно условию, h₂=4,5h₁, а₁=3а₂. Объем призмы равен: V=S_оснh. Т.к. в основании коробок лежит квадрат, то S_осн=а². Отсюда: V=a²h. Для 1-й коробки имеем: V₁=a₁²h₁. Для 2-й коробки: V₂=a₂²h₂. Тогда получаем отношение:

Ответ: 2

Вариант 13МБ10

В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.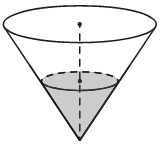

Алгоритм выполнения

Доказываем, что данные в условии конусы подобны.
Определяем коэффициент подобия.
Используя свойство для объемов подобных тел, находим объем жидкости.

Решение:

Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.

По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.

Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V₁, малого – V₂. Получим: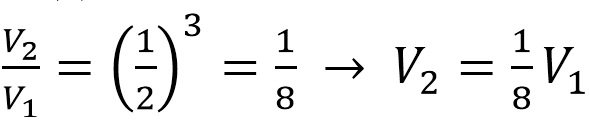

.

Поскольку по условию V₁=1600 мл, то V₂=1600/8=200 мл.

Вариант 13МБ11

Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?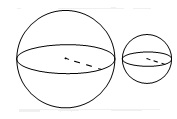

Алгоритм выполнения

Записываем формулу для вычисления объема шара.
Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.

Решение:

Объем шара вычисляется по ф-ле:

. Отсюда объем 1-го (большего) шара равен

, 2-го (меньшего) шара –

. Составим отношение объемов:

Подставляем в полученную формулу числовые данные из условия:

Вывод: объем большего шара в 64 раза больше.

Вариант 13МБ12

Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

Алгоритм выполнения

Записываем формулу для определения площади бок.поверхности цилиндра.
Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.

Решение:

Площадь бок.поверхности цилиндра вычисляется так: S=2πRH. Для 1-го цилиндра имеем: S₁=2πR₁H₁. Для 2-го цилиндра: S₂=2πR₂H₂. Составим отношение этих площадей:

Найдем числовое значение полученного отношения:

Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.

Вариант 13МБ13

Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?

Алгоритм выполнения

Записываем формулу для определения массы большего шаров через плотность и объем.
Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.

Решение:

Масса большего (1-го) шара равна: m₁=ρV₁. Объем этого шара составляет V₁=(4/3)πR₁³. Отсюда получаем: m₁=(4/3)πρR₁³. Из этого уравнения выразим плотность:

. Масса меньшего (2-го) шара равна: m₂=ρV₂. Объем шара: V₂=(4/3)πR₂³. В ур-ние для m₂ подставим выражения для ρ и V₂. Получаем:

Вычисляем m₂: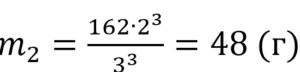

Вариант 13МБ14

В бак, имеющий форму правильной четырехугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.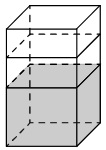

Алгоритм выполнения

Определяем часть призмы, соответствующую объему погруженной детали.
Вычисляем объем детали на основании формулы для определения объема прямой призмы с квадратом в основании.

Решение:

Погруженная в жидкость деталь занимает объем, соответствующий столбу жидкости, высота которого равна 10 см, т.е. разнице, возникшей между начальной высотой жидкости и конечной (после погружения). Это означает, что деталь имеет объем, равный части жидкости, занимающей объем 40х40х10 (см).

Найдем этот объем:

V=40·40·10=16000 (см³).