ҚМЖ. 11 есеп.жарат.Закирова (1). 1. Шарик совершает гармонические колебания с амплитудой 0,1 м. В начальный момент времени он находится в положении равновесия. Определите смещение шарика от положения равновесия в момент вре мени, равный t T12 (периода)
 Скачать 4.83 Mb. Скачать 4.83 Mb.
|
|
Упр 1 1. Шарик совершает гармонические колебания с амплитудой 0,1 м. В начальный момент времени он находится в положении равновесия. Определите смещение шарика от положения равновесия в момент вре- мени, равный t = T/12 (периода).  2. Грузик, прикрепленный к пружине, совершает гармонические колебания с амплитудой 0,1 м и периодом 1,57 с. Определите максимальное уско- рение грузика во время его движения. Ответ: 1,6 м/с² Объяснение: Проанализируем формулу для координаты грузика: Ускорение грузика совпадает со второй производной координаты грузика по времени: Хорошо видно, что амплитуда ускорения грузика: С учетом того, что , имеем: 3. Частота незатухающих колебаний струны составляет 5 Гц. Амплитуда коле- баний некоторой точки на струне 1 мм. Какой путь пройдет эта точка за 5 с? Ответ: 100 мм Объяснение: За одно полное колебание точка пройдем путь, равный учетверенной амплитуде ее колебаний, т.е. равный 4*1=4 мм, в течении 5 с струна совершит: Пройденный точкой путь: 4*. Человек массой 80 кг наступил на плоскую льдину, плавающую в воде, и льдина вместе с человеком начала колебаться с периодом 2 с. Опреде- лите толщину льдины, если площадь ее верхней поверхности равна 1 м 2 , а плотность льда – 900 кг/м 3 . Дано: h = 40 см = 0,40 м m = 80 кг _______________ S - ? Объем льдины:V =S*h 2)Сила Архимеда на льдину:Fa = ρ*g*V (1) 3) Масса льдины:m₁=ρ₁*V 3) Сила тяжести, действующая на льдину вместе с грузом F = m*g + ρ₁*V*g =g*(m+ρ₁*V) (2) Поскольку льдина плавает, то приравниваем (1) и (2) ρ*g*V =g*( m+ρ₁*V) ρ*V = m+ρ₁*V V = m/(ρ-ρ₁) Площадь льдины: S = m / ((ρ-ρ₁)*h) = 80 / ((1000-900)*0,4) = 2 м² (Замечание плотность воды 1000 кг/м³,плотность льда 900 кг/м³) 5. Материальная точка совершает колебания по закону: х = 0,4 cos p (2t + 1/2). Постройте график зависимости координаты точки от времени. Материальная точка совершает колебания по законух = 0,02соs(пt+п/2) м.. Определить: 1) амплитуду колебаний;2) период колебаний; 3) начальную фазу колебаний; 4) Максимальную скорость точки; 5) максимальное ускорение точки; 6) спустя какое время после начала отсчета точка будет проходить через положение равновесия. Решение. х (t) = 0,02*соs(п*t+п/2) м; x0=0,02; (2*pi)/T=pi; T=0,5; u0=pi/2; v(t)=-0,02*pi*sin(pi*t+pi/2); vm=0,02*pi; a(t)=-0,02*(pi^2)*cos(pi*t+pi/2); am=-0,02*(pi^2); x(t)=0; 0,02*соs(п*t+п/2)=0; pi*t+pi/2=pi/2; t=0; В начале колебания. Упр 2 1. При индуктивности колебательного контура 100 мкГн частота свободных электрических колебаний равна 2 МГц. Какой должна быть индуктивность контура при неизменной электроемкости, чтобы частота колебаний в контуре стала равной 4 МГц? T₁ = 2π√ (L₁·C) T₂ = 2π√ (L₂·C) Найдем: T₂ / T₁ = √ (L₂ / L₁) Но υ ₁ = 1 / T₁ υ ₂ = 1 / T ₂ υ₁ / υ₂ = T₂ / T₁ 2 / 4 = √ (L₂ / L₁) (1/2)² = L₂ / L₁ L₂ = L₁· (1/4) = 100 / 4 = 25 мкГн 2. Колебательный контур состоит из катушки индуктивности и двух оди- наковых конденсаторов, включенных параллельно. Во сколько раз уве- личится частота свободных электрических колебаний в контуре, если конденсаторы включить последовательно? T=2*π*√(L*C) Параллельное соединение - емкость 2С Последовательное - емкость С/2 Период уменьшится в 2 раза а частота увеличится в 2 раза 3. Как надо изменить расстояние между пластинами конденсатора в колебательном контуре, чтобы частота колебаний увеличилась в 2 раза? Частота контура обратно пропорциональна корню из величины электроёмкости конденсатора. Чтобы частота контура увеличилась в 2 раза емкость конденсатора нужно уменьшить в 4 раза. Поскольку емкость конденсатора обратно пропорциональна расстоянию между пластинами, и прямо пропорциональна площади пластин, надо либо пластины раздвинуть на расстояние, в 4 раза большее первоначального. Либо сместить пластины друг относительно друга, чтобы площадь перекрытия уменьшилась в 4 раза... 4*. Определите период колебаний в контуре,изображенном на рисунке 19. В контур подключены два идеальных полупроводниковых диода. С = 0,25 мкФ, L 1 = 2,5 мГн,L 2 = 4,9 мГн.  Упр 3 1. Определите потенциальную энергию пружины при смещении груза массой 0,1 кг от положения равновесия на 0,03 м. Циклическая частота гармонических колебаний 20 рад/с. Дано: m=0,1 кг; ω=20 с⁻¹; х=0,03 м;__________ Еп-? Решение: Собственная частота колебаний пружинного маятник: , где k - жесткость пружины, выразим её: Теперь можно найти потенциальную энергию деформированной пружины: 2. Определите полную энергию колебательного контура с конденсатором электроемкостью 10 пФ. Максимальное напряжение на обкладках конден- сатора достигает 100 В. В колебательном контуре при максимальном напряжении на конденсаторе концентрируется максимальная электрическая энергия Eэ=C*Um^2/2 В СИ С=10*10^-12 Ф=10^-11 Ф Emэ=10^-11*100^2/2=5*10^-8 Дж В контуре происходит периодический процесс перехода электрической энергии конденсатора, в энергию магнитного поля катушки. Когда энергия конденсатора равно 0, энергия катушки достигает максимального значения. Поэтому по закону сохранения энергии Emм=Emэ=5*10^-8 Дж 3*. Пружинный маятник с грузом массой 0,81 кг, вывели из состояния равно- весия. Определите жесткость пружины, если через 0,314 с его смещение от положения равновесия впервые стало равным половине амплитуды колебаний.  4*. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5 мА, а амплитуда заряда конденсатора 2,5 нКл. В некоторое время заряд конденсатора стал равным 1,5 нКл. Определите силу тока в катушке в этот момент. В идеальном колебательном контуре в катушке индуктивности амплитуда колебаний силы тока Iм = 5 мА, а амплитуда колебаний заряда конденсатора qм = 2,5 нКл. В момент времени t сила тока в катушке i=3мА. Найдите заряд конденсатора в этот момент. L*Im^2/2=qm^2/2*C LC=qm^2/Im^2=6,25*10^-18/25*10^-6=0,25*10^-18 В момент времени t: qm^2/2*C=q^2/2*C+L*I^2/2 qm^2=q^2+l*C*I^2 q=sqrt(qm^2-L*C*I^2)=(6,25*10^-18-0,25*10^-18*9*10^-6)=2*10^-9 Кл=2 нКл 5. Емкость конденсатора колебательного контура 0,4 мкФ, частота соб- ственных колебаний 50 кГц, амплитуда колебаний заряда 8 мкКл. Запи- шите уравнения q = q(t), u = u(t), i = i(t). Определите амплитуду колебаний напряжения, амплитуду колебаний силы тока и индуктивность катушки. Постройте графики зависимости величин. 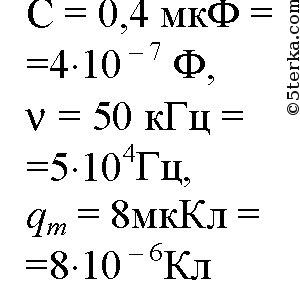 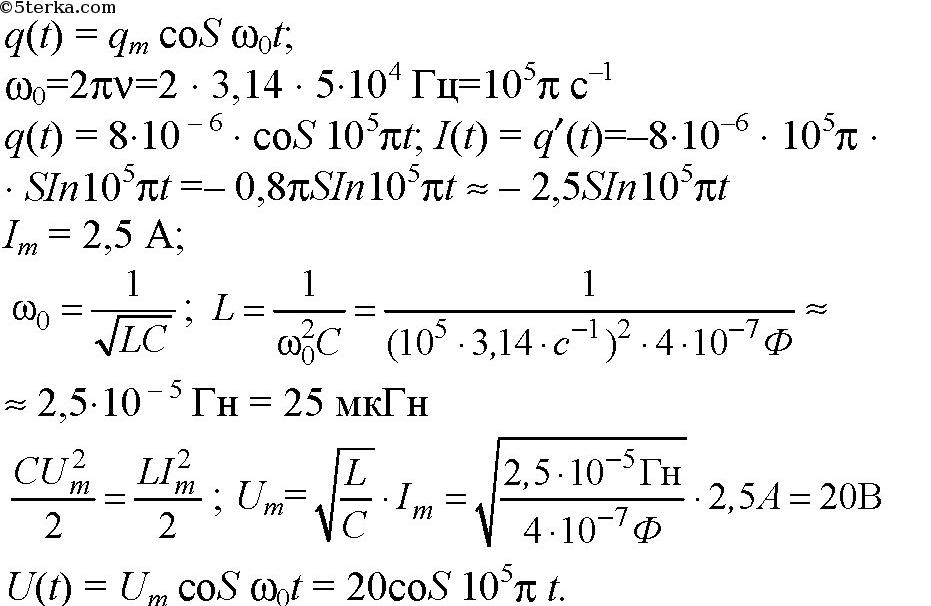 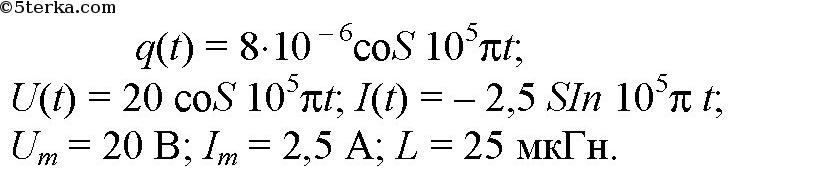 6. Напряжение на обкладках конденсатора емкостью 1 мкФ меняется по закону: u = 100cos500t. Определите: а) максимальное значение напря- жения на конденсаторе; б) период, частоту и циклическую частоту коле- баний в контуре; в) максимальный заряд конденсатора; г) индуктивность контура; д) максимальную силу тока в контуре. Напишите: е) уравнение зависимости заряда конденсатора от времени; ж) уравнение зависимости силы тока от времени. Изобразите графики зависимости u(t), q(t), i(t). C=1 мкФ =1*10^-6 Ф, U =100 cos 500t (В). а) Um=100 В. б) T=2π/ω=6.28/500=0,01256 c. v=1/T=79,6 Гц. ω=500 Гц. в) qm=C*Um = 1*10^-6* 100 = 1*10^-4 Кл. г) ω=1/√(LC), ω^2LC=1, L=1/(Cω^2) = 1/(25*10^4*10^-6) = 4 Гн. д) Im=qm*ω, Im=1*10^-4* 500=0,05 А. е) q=C*U=10^-4*cos500t. ж) i=q'=-500*10^-4*sin500t =0,05 cos(500t+π/2). Упр 4 1. Рамку с площадью S = 200 см 2 вращают с частотой ñ = 8 с –1 в магнитном поле с индукцией В = 0,2 Тл (рис. 30). Напишите: а) закон изменения магнитного потока, пронизывающего рамку; б) закон изменения ЭДС индукции, возникающий в рамке. В начальный момент времени рамка перпендикулярна магнитному полю. Рамка площадью 200 см2 вращается с частотой 8 с-1 в магнитном поле индукцией 0,4 Тл. Написать уравнения Ф = Ф(t) и е = e(t), если при t = 0 нормаль к плоскости рамки перпендикулярна линиям индукции поля. Найти амплитуду ЭДС индукции. 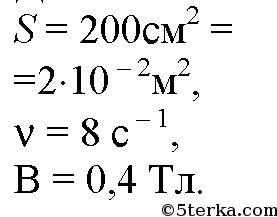 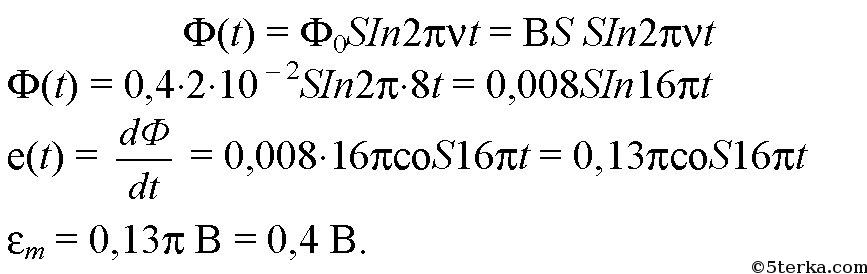 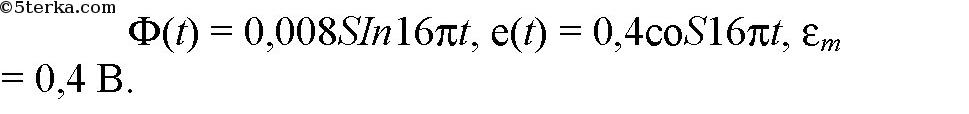 2. По графику определите амплитудное значение переменной ЭДС, ее период и частоту. Запишите закон изменения ЭДС с течением времени. 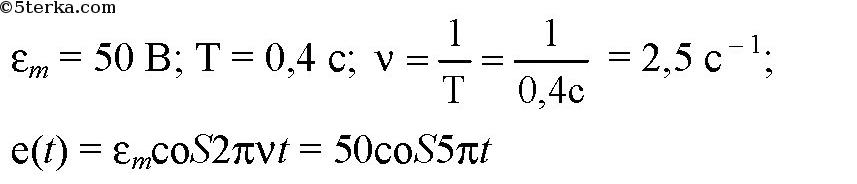 3. Генератор переменного тока имеет на роторе восемь пар полюсов n = 8. Какой должна быть частота вращения ротора, чтобы генератор вырабатывал ток стандартной частоты n = 0 Ãö 50 Гц? Генератор переменного тока имеет на роторе 6 пар полюсов. Какой должна быть частота вращения ротора, чтобы генератор вырабатывал ток стандартной частоты? f=(p*n)/60 где n — число оборотов ротора в минуту, р - количество пар полюсов, f-частота ( у нас 50 герц) n=60f/p=(60*50)/6=3000/6= 500 об/мин Упр 5 1. Сила тока в цепи меняется по закону i t = + 8 5 314 0 661 , sin( , ) . Определите амплитудное значение силы тока, его начальную фазу и частоту.  2. Напряжение на концах участка цепи переменного тока изменяется по синусоидальному закону. Начальная фаза ϕ=π/03 , период колебаний T = 0,02 с. В момент времени t=T/24 напряжение u = 5 В. Определите: амплитуду напряжения, циклическую частоту, частоту тока. Запишите закон изменения напряжения с течением времени. Дано: U=U0sin(ωt+π6), t=T12, U=10 В, U0−? Решение задачи: Циклическая частота колебаний ω связана с периодом колебаний T по следующей формуле: ω=2πT Запишем с учётом этого данное в условии уравнение колебаний напряжения для момента времени t=T12: U=U0sin(2πT⋅T12+π6) U=U0sin(π3) Откуда амплитуда колебаний напряжения U0 равна: U0=Usin(π3) Посчитаем численный ответ задачи: U0=10⋅23–√=11,55В 3*. Сила тока в цепи изменяется со временем по закону i=4 sin (314t+ π/6 Определите: действующее значение силы тока, его начальную фазу и период колебаний тока. Чему будет равна сила тока в моменты времени: t 1 = 0,01 с, t 2 = 0,04 с? Сила тока в цепи изменяется по закону i=0,85sin(314t+0.651).Определить действующее значение силы тока, его начальную фазу и частоту. Чему равна сила тока в цепи в момент времени 0,08с? I (действ)=Imax (амплитудное)/корень из 2 из формулы i=Imsin(омега*t+фи нулевое) I действ = 0.85/корень из 2 = 0,6 A начальная фаза фи0=0.651 частота ню= омега/2*пи=50 Гц i(0,08)=0,37А график - синусоида, координаты можно найти подстановкой t в данное уравнение Упр 6 1. На участке цепи с активным сопротивлением R = 4 Ом сила тока изме- няется по закону i = 6,4sin314t. Определите действующее значение силы тока. Запишите зависимость напряжения от времени.  2. Определите емкость конденсатора, включенного в сеть переменного тока стандартной частоты n ст = 50 Гц с напряжением U = 220 B, если сила тока в цепи I = 2 A. 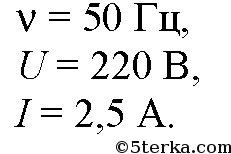 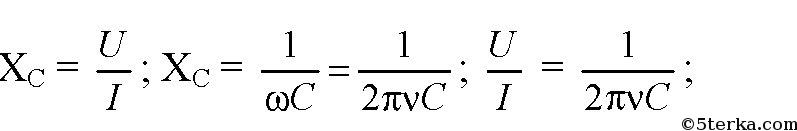 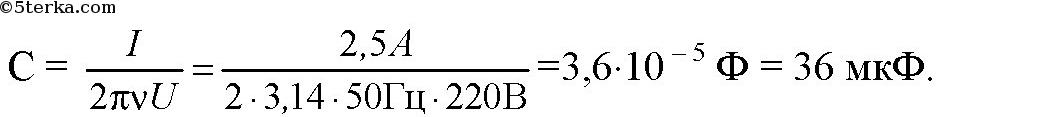 3. Катушка индуктивностью L = 35 мГн включена в сеть переменного тока. Определите ее сопротивление при частоте тока n = 50 Гц. |
