физика. заготовка. Найдем момент инерции системы относительно оси вращения
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
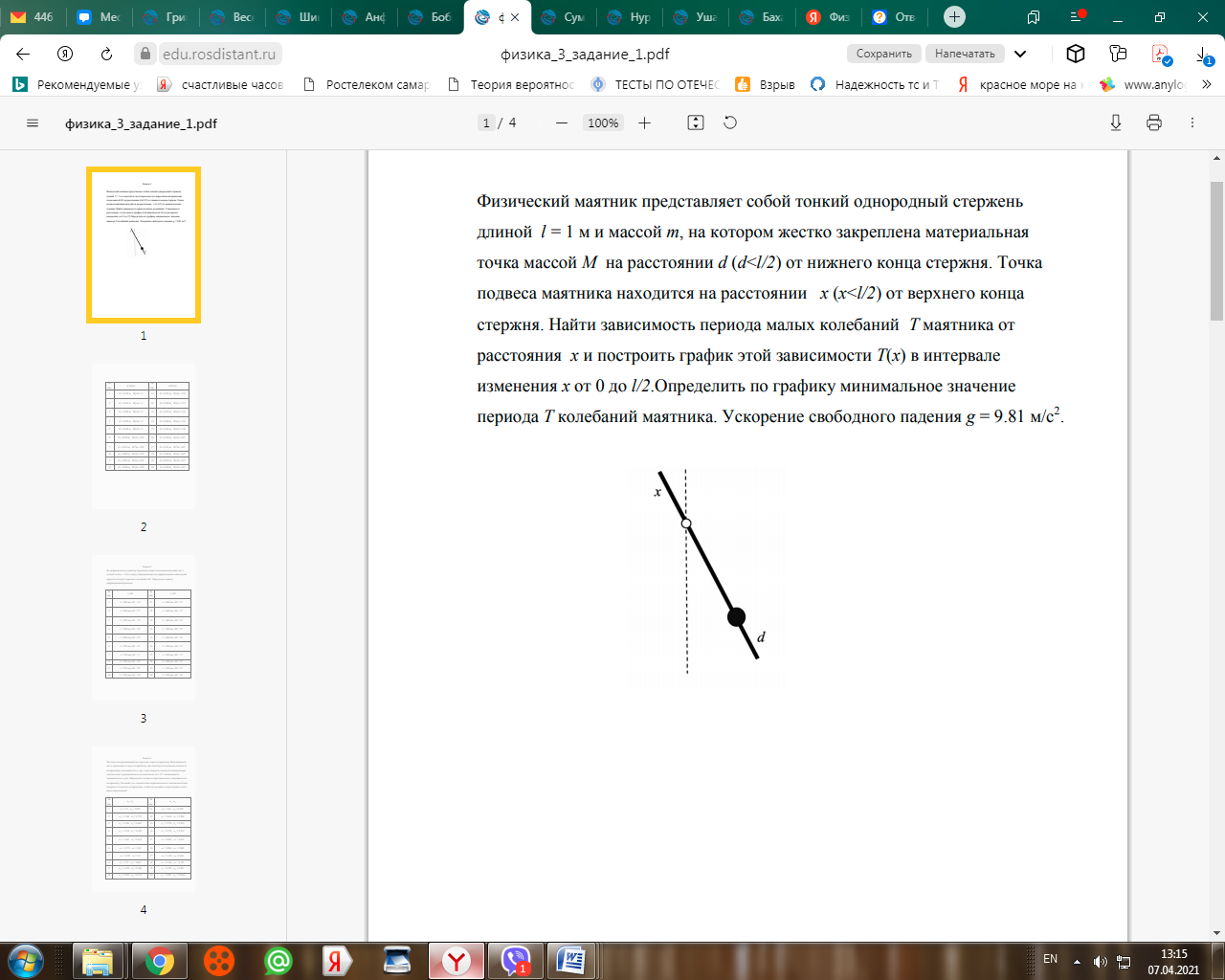 Физический маятник представляет собой тонкий однородный стержень длиной l = 1 м и массой m, на котором жестко закреплена материальная точка массой M на расстоянии d (d < l/2) от нижнего конца стержня. Точка подвеса маятника находится на расстоянии x (x < l/2) от верхнего конца стержня (рис. 1). Найти зависимость периода малых колебаний T маятника от расстояния x и построить график этой зависимости T(x) в интервале изменения x от 0 до l/2. Определить по графику минимальное значение периода T колебаний маятника. Ускорение свободного падения g = 9.81 м/c2. Дано: d=0,10м, M/m=0,7. Найдем момент инерции системы относительно оси вращения. Расстояние от груза до оси вращения: (L-x-d) Значит момент инерции груза относительно оси: M (L-x-d)^2 Момент инерции стержня длинной L массой m относительно центра: (1/12) m L^2 Расстояние между центром стержня и осью вращения: L/2 - x Тогда по теореме Штейнера, момент инерции стержня относительно оси вращения: (1/12) m L^2 + m (L/2 - x)^2 = m ( L^2 / 3 - Lx - x^2) Момент инерции для всей системы: M (L-x-d)^2 + m ( L^2 / 3 - L x - x^2 ) 2) Найдем момент сил относительно оси вращения: Сила, действующая на грузик: M g Плечо этой силы: (L - x - d) sin(ф) Тогда момент силы, действующей на грузик: M g (L - x - d) sin(ф) Стержень разделим на две части. a) Длина части стержня, находящейся под осью вращения: L - x Масса этой части: m (L - x) / L Тогда сила тяжести, действующая на эту часть стержня: m g (L - x) / L Центр масс этой части находится на расстоянии от оси: (L - x) / 2 Плечо силы тяжести: (L - x) sin(ф) / 2 Момент силы тяжести, действующий на часть под осью вращения: m g (L - x)^2 sin(ф) / (2 L) б) Длина части стержня, находящейся над осью вращения: x Масса этой части: m x / L Тогда сила тяжести, действующая на эту часть стержня: m g x / L Центр масс этой части находится на расстоянии от оси: x / 2 Плечо силы тяжести: x sin(ф) / 2 Момент силы тяжести, действующий на часть под осью вращения: m g x^2 sin(ф) / (2 L) (Т. к. эта часть момента сил пытается вращать стержень в другом направлении, ей припишем знак -) Тогда полный момент сил: ( M [L - x - d] + m [(L - x)^2 - x^2] / [2 L]) g sin(ф) = ( M [L - x - d] + m [L/2 - x] ) g sin(ф) 3) Запишем уравнение движения: J ф'' = N (J - момент инерции, N - момент сил) (момент записали со знаком -, т. к. он должен быть отрицательным при положительных ф и наоборот) {M (L-x-d)^2 + m ( L^2 / 3 - L x - x^2 )} ф'' = - ( M [L - x - d] + m [L/2 - x] ) g sin(ф) Для ф получаем уравнение: ф'' + { ( M [L - x - d] + m [L/2 - x] ) / ( M [L - x - d]^2 + m [ L^2 / 3 - L x - x^2 ] ) } g sin(ф) =0 Т. е. уравнение вида: ф'' + w^2 sin(ф) = 0 w^2 = { ( M [L - x - d] + m [L/2 - x] ) / ( M [L - x - d]^2 + m [ L^2 / 3 - L x - x^2 ] ) } g Разделим числитель и знаменатель на m, преобразуем: w^2 = g (A - Bx) / (C - Dx - Ex^2) A = (M/m)(L-d) + L/2 = 1.13 (м) B = 1 + M/m = 1.7 C = (M/m) (L-d)^2 + L^2 / 2 = 1.067 (м^2) D = 2(M/m) (L-d)+L = 2.26(м) E = 1 w^2 = 9.81 (1.13 - 1.7 x) / (1.067 - 2.26 x - x^2) Дальше T = 2 п / w Дано: d=0,15м, M/m=1. 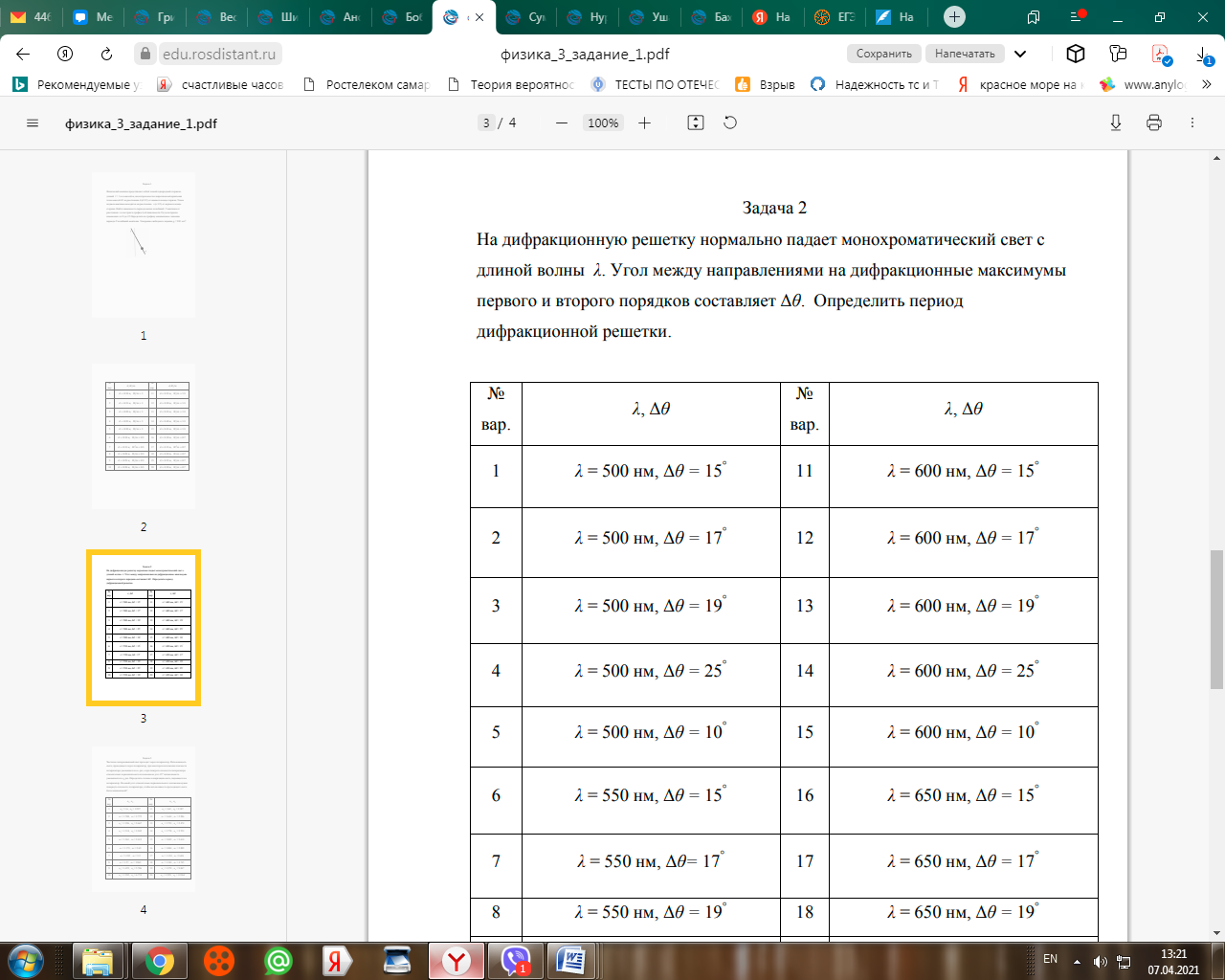 Условие интерференционных максимумов дифракционной решётки имеет вид где — порядок дифракции. Выразим период дифракционной решётки из этой формулы и, используя любые два соответственных значения и из таблицы, найдём его: Задача 3 Частично поляризованный свет проходит через поляризатор. Интенсивность света, проходящего через поляризатор, при некотором положении плоскости поляризатора уменьшается в n1 раз, а при повороте плоскости поляризатора относительно первоначального положения на угол 45° интенсивность уменьшается в n2 раз. Определить степень поляризации света, падающего на поляризатор. На какой угол относительно первоначального положения нужно повернуть плоскость поляризатора, чтобы интенсивность проходящего света была минимальной? 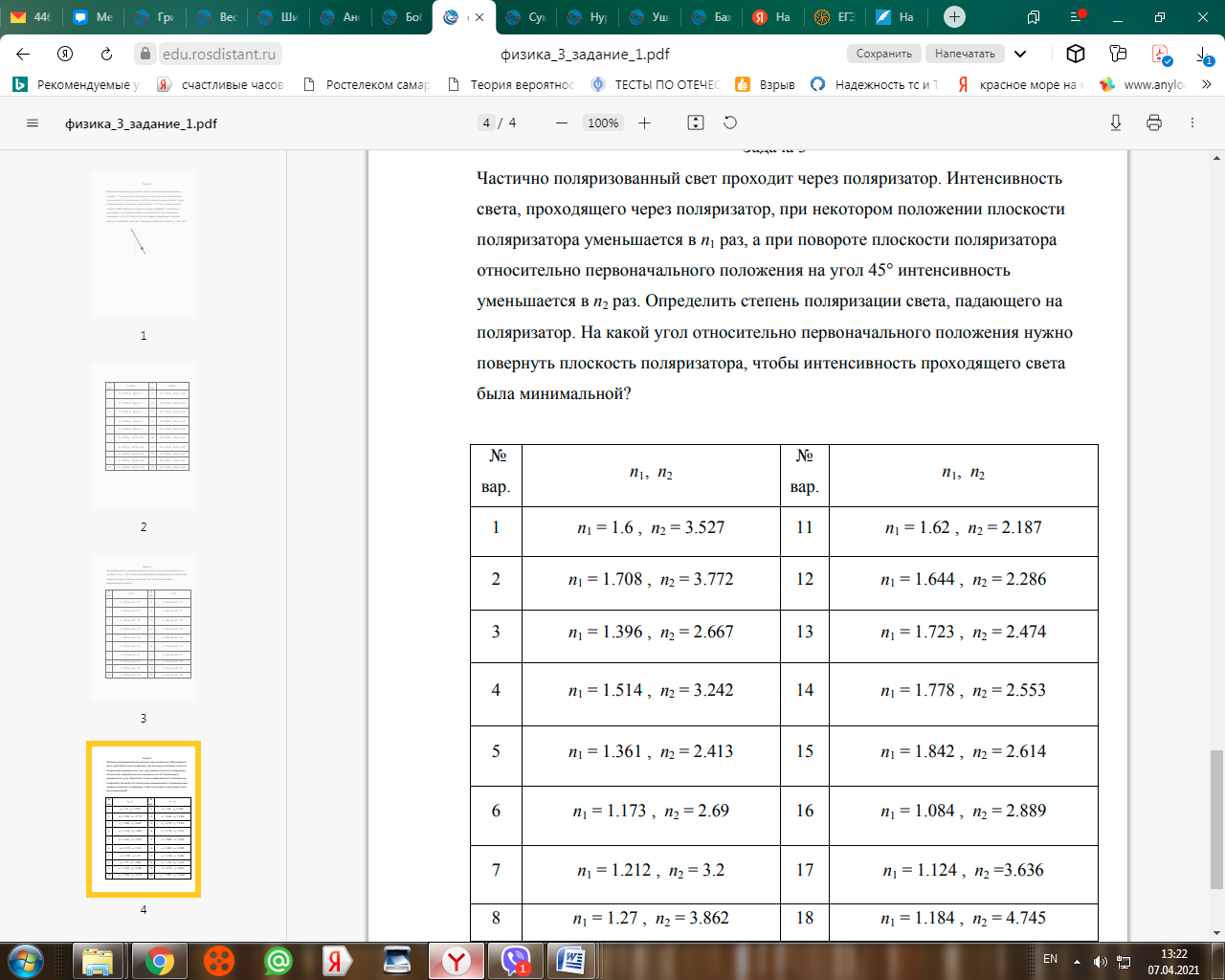 |
