Вариант 1
|
1
|
Для ремонта квартиры требуется 37 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?
|
2
3
|
Найдите значение выражения 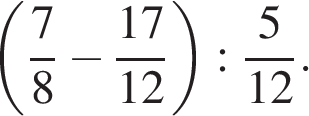
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
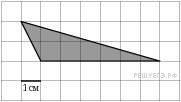
|
4
|
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
|
5
|
Решите уравнение: 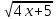 = 5 = 5
|
6
7
8
9
|
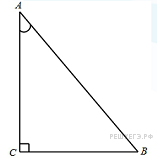
В треугольнике АВС угол С равен 90°, АС=9,sinА= 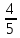 . Найдите АВ. . Найдите АВ.
Найдите значение выражения 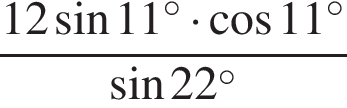
Площадь поверхности куба равна 18.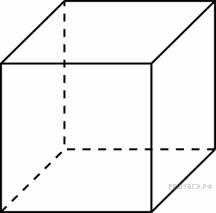
Найдите его диагональ.
Из пункта A в пункт B одновременно выехали два
автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со
скоростью, на 16 км/ч большей скорости первого, в
результате чего прибыл в пункт B одновременно с
первым автомобилем. Найдите скорость первого
автомобиля. Ответ дайте в км/ч.
|
Часть 2
11 а) Решите уравнение 
б) Найдите все корни уравнения, принадлежащие отрезку 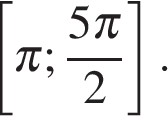
12 В правильной шестиугольной пирамиде SABCDEF
стороны основания которой равны 1, а боковые ребра
равны 2, найдите косинус угла между прямыми SB
и AD.
|
13
|
Решите неравенство: 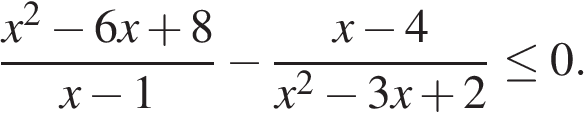
|
|
|
|
|
|
Вариант 2
|
1
|
Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?
|
2
3
|
Найдите значение выражения 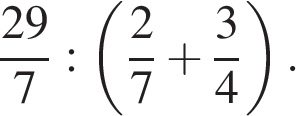
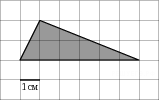
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
|
4
|
В фирме такси в данный момент свободно 16 машин: 4 черных, 3 синих и 9 белых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет черное такси.
|
5
|
Решите уравнение: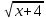 = 7 = 7
|
6
7
8
9
|
В треугольнике АВС угол С равен 90°, АС=4,sinА= 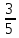 . Найдите АВ. . Найдите АВ.

Найдите значение выражения: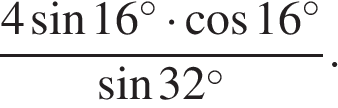

Площадь поверхности куба равна 8.
Найдите его диагональ.
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27 км/ч, а вторую половину пути — со скоростью, на 18 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
|
Часть 2
При выполнении заданий 13 –15 необходимо
записать полное обоснованное решение и ответ.
|
11
|
а) Решите уравнение 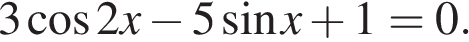
б) Укажите корни этого уравнения, принадлежащее отрезку 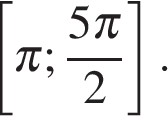
|
12
|
В правильной шестиугольной пирамиде SABCDEF
стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB
и AD.
|
|
13
|
Решите неравенство: 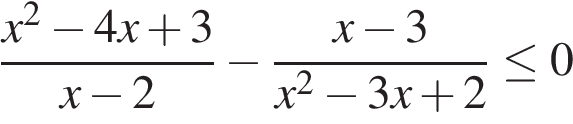
|
Ответы и решения
Вариант 1
Часть 1:
№
п/п
|
Ответ
|
1
|
7
|
2
|
20
|
3
|
-1,3
|
4
|
6
|
5
|
0,4
|
6
|
5
|
7
|
5
|
8
|
15
|
9
|
6
|
10
|
3
|
11
|
32
|
12
|
2,5
|
Вариант 2
Часть 1:
№
п/п
|
Ответ
|
1
|
11
|
2
|
-14
|
3
|
4
|
4
|
6
|
5
|
0,25
|
6
|
45
|
7
|
3
|
8
|
5
|
9
|
2
|
10
|
2
|
11
|
36
|
12
|
2
|
Часть 2:
13. а) Решите уравнение 
б) Найдите все корни уравнения, принадлежащие отрезку 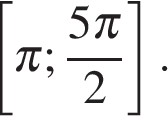
Решение.
а) Преобразуем уравнение:
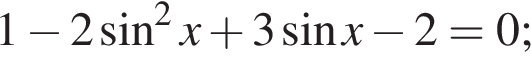
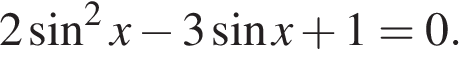
Получаем 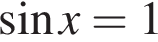 или или 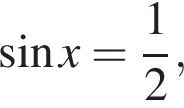 откуда откуда 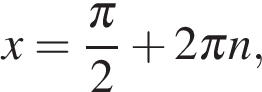 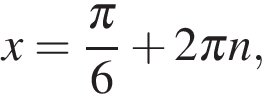 или или 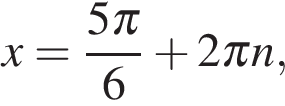 где где 
б) На отрезке 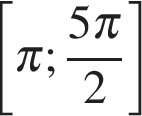 корни отберём с помощью единичной окружности. корни отберём с помощью единичной окружности.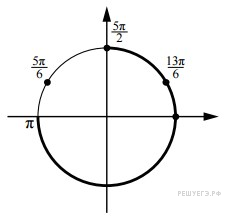
Получаем 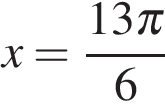 и и 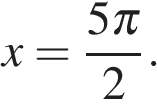
Ответ: а) 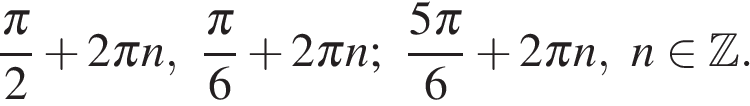
б) 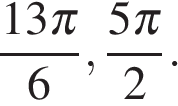
Баллы
|
Критерии оценки выполнения задания
|
3
|
Обоснованно получен правильный ответ
|
2
|
Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку
|
1
|
Тригонометрическое уравнение решено, но допущена вычислительная ошибка
|
0
|
Решение не соответствует ни одному из критериев
|
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая AD параллельна прямой BC. Следовательно, искомый угол — SBC. В равнобедренном треугольнике SBC проведём медиану и высоту SM. Имеем:
Из прямоугольного треугольника SBM
получаем:
Ответ:
15. Решите неравенство: 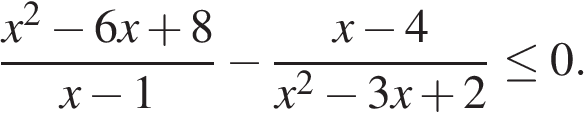
Решение.
Перепишем неравенство в виде:
Множество решений исходного
неравенства:
Ответ:
Баллы
|
Критерии оценки выполнения задания
|
2
|
Обоснованно получен верный ответ
|
1
|
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно
|
0
|
Другие случаи, не соответствующие указанным критериям
|
2
|
Максимальный балл
|
Вариант 2
Часть 1:
№
п/п
|
Ответ
|
1
|
11
|
2
|
-14
|
3
|
4
|
4
|
6
|
5
|
0,25
|
6
|
45
|
7
|
3
|
8
|
5
|
9
|
2
|
10
|
2
|
11
|
36
|
12
|
2
|
Часть 2:
13. а) Решите уравнение 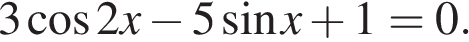
б) Укажите корни этого уравнения, принадлежащее
отрезку 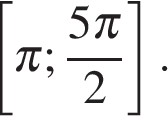
Решение.
Сведём уравнение к квадратному относительно синуса, используя
формулу Имеем:
б) С помощью числовой окружности отберём корни, принадлежащие
отрезку , получим число
Ответ:
а) б)
Баллы
|
Критерии оценки выполнения задания
|
3
|
Обоснованно получен правильный ответ
|
2
|
Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку
|
1
|
Тригонометрическое уравнение решено, но допущена вычислительная ошибка
|
0
|
Решение не соответствует ни одному из критериев
|
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая параллельна прямой Следовательно, искомый угол — В равнобедренном треугольнике проведём
медиану и высоту
Имеем:
Из прямоугольного треугольника
получаем:
Ответ:
Баллы
|
Критерии оценки выполнения задания
|
2
|
Обоснованно получен верный ответ
|
1
|
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно
|
0
|
Другие случаи, не соответствующие указанным критериям
|
2
|
Максимальный балл
|
15. Решите неравенство: 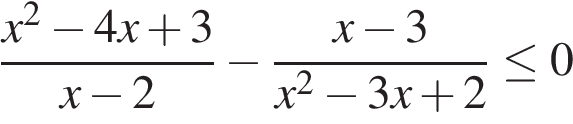
Решение.
Перепишем неравенство в виде:
Таким образом, множество решений исходного неравенства:
Ответ:
Баллы
|
Критерии оценки выполнения задания
|
2
|
Обоснованно получен верный ответ
|
1
|
Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно
|
0
|
Другие случаи, не соответствующие указанным критериям
|
2
|
Максимальный балл
|
Критерии оценки выполнения
Общий балл формируется путем суммирования баллов, полученных учащимися за выполнение заданий. За каждое верно выполненное задание части 1 начисляется 1 балл, за каждое задание части 2 – 2 балла.
Оценка работы:
Балл
|
Отметка
|
14-18
|
5
|
9-13
|
4
|
6-8
|
3
|
0-5
|
2
| |
 Скачать 166.94 Kb.
Скачать 166.94 Kb.




