хз. Найти неопределенные интегралы
 Скачать 46.58 Kb. Скачать 46.58 Kb.
|
ИДЗ 8.2 – Вариант 8Найти неопределенные интегралы.  1.8 1x dx 1.8 1x dxРазобьем интеграл на два интеграла    1x dx 1 dx x dx 1x dx 1 dx x dxПервый интеграл, табличный:  Применима табличная формула интегрирования: dx arcsin x C Применима табличная формула интегрирования: dx arcsin x C a   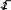 1 dx 1 dx arcsinx C 1 dx 1 dx arcsinx CВторой интеграл: Проведем замену: t = 2 − x2, dt = (2 − x2)′dx = −2xdx, dx dt 2x , тогда x 1 1 1 1 1 dx dt t 2 dt 1 1 t 2 1 C 1 t 2 C C  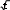 2 2 2 2 2 2 1 1 2 1 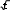 2 2 2 2Учли, в решении интеграла, табличный интеграл x Проведем обратную замену: t = 2 − x2 В итоге решение интеграла примет вид: x1 dx 1 C   x dx C x dx CТогда решение исходного интеграла примет вид:  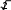  1x dx arcsinx C 1x dx arcsinx C 2.8 sin 2x dx 3sin 2 x 4 В числителе используем формулу двойного угла sin2x = 2sinxcosx, запишем интеграл: sin2x dx 2sinxcosx dx 3sin 2 x 4 3sin 2 x 4 Интегрирование заменой переменной (метод подстановки) f xf xdx t f x dt f xdx tdt Проведем замену: t = sinx, dt = (sinx)′dx = cosxdx, dx dt cos x , тогда sin2x tdt 2 d3t 2 4 1 2 3sin 2 x 4 dx 2 3t 2 4 6 3t 2 4 ln 3t 3 4 C Учли, в решении интеграла, табличный интеграл Проведем обратную замену: t = sinx В итоге решение интеграла примет вид: sin2x dx 1 ln 3sin 2 x 4 C dx lnx С x 3sin 2 x 4 3 x 5 3.8 1 x3 dx 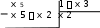 Разделив числитель подынтегральной функции на знаменатель, выделим целую часть неправильной дроби, стоящей под знаком интеграла. Получим интеграл от алгебраической суммы: Разделив числитель подынтегральной функции на знаменатель, выделим целую часть неправильной дроби, стоящей под знаком интеграла. Получим интеграл от алгебраической суммы:x 2 Тогда интеграл запишется в виде x 5 1 x 2 3 dx x x 2 1 x 3 dx x 2dx x 2 1 x 3 dx Первый интеграл, табличный: Применима табличная формула интегрирования: x x1 dx 1 C x 2 x 21 x3 dx C C 2 1 3 Второй интеграл Проведем замену: t = 1 − x3, dt = (1 − x3)′dx = −3x2dx, dx dt 3x 2 , тогда x 2 1 dt 1 1 x3 dx 3 t lnt C 3 Учли, в решении интеграла, табличный интеграл Проведем обратную замену: t = 1 − x3 В итоге решение интеграла примет вид: dx lnx С x x 2 1 3 1 x3 dx 3 ln1 x C Тогда решение исходного интеграла примет вид: x x 5 3 1 x3 dx 3 1 ln1 x3 C 3 4.8 cos x 32 dx Подынтегральную функцию раскроем как квадрат суммы cos x 32 dx cos2 x 6cos x 9dx cos2 xdx 6cos xdx 9dx Используем формулу половинного угла cos 2 x 1 cos 2x 2 Решаем интеграл cos x 32 dx 1cos2x dx 6 cos xdx 9dx 1 dx 1 cos 2xdx 6sin x 9x 2 2 2 1 x 1 1 sin 2x 6sin x 9x C 19 x 1 sin 2x 6sin x C 2 2 2 2 4 Применили в решении табличную формулу интегрирования: cos xdx sin x C 5.8 tg2 x dx 2 Согласно тригонометрическому тождеству tg2 x sin 2 x 2 и sin 2 x 1 cos2 x , преобразуем и решаем интеграл sin 2 x 1 cos 2 x 2 cos 2 x 2 2 2 cos 2 x tg2 xdx 2 dx 2 dx 1 dx 2 dx 1 dx dx 2 cos 2 x 2 cos 2 x 2 cos 2 x 2 cos 2 x 2 cos 2 x 2 21 d x x 2tg x x C 2 x 2 2 cos 2 Применили в решении табличную формулу интегрирования: dx tgx C cos 2 x 6.8 sin x cos 3x dx 2 2 Используя формулу произведения тригонометрических функций sin cos 1 sin sin , 2 преобразуем, затем решим интеграл sin x 3x sin x 3x x 3x 2 2 2 2 1 1 1 sin cos 2 dx dx 2 2 2 sin x sin 2xdx 2 sin xdx 2 sin 2xdx 1 cos x 1 1 sin 2xd 2x 1 cos x 1 cos 2x C 1 cos x 1 cos 2x C 2 2 2 2 4 2 4 Применили в решении табличную формулу интегрирования: sin xdx cos x C 7.8 dx 2x 2 x 2 Вынесем 2 за скобку в знаменателе dx dx 2 2x 2 x 2 x 2x 1 2 Преобразуем интеграл, выделим в знаменателе подынтегральной функции полный квадрат (формула квадрата суммы (a + b)2 = a2 + 2ab + b2) 2 x 2 1 1 2 1 2 2 1 1 1 1 2 15 x 1 x 2 x 1 x 2 x 1 x 2 4 Решаем интеграл 4 4 4 16 16 4 16 x 1 4 dx dx 1 dx 1 dx 1 4 arctg 4 C 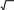 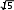 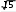 2x 2 x 2 2x 2 x 2 2 x 2 1 2 15 2 1 2 15 2 2 2 x 1 2 x x 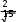 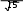 arctg 4x 1 C arctg 4x 1 C 4 16 4 4 Применили в решении табличную формулу интегрирования: dx 1 arctg x C x 2 a 2 a a  8.8 dx 8.8 dx Преобразуем интеграл, выделим в знаменателе подынтегральной функции полный квадрат (формула квадрата разности (a − b)2 = a2 − 2ab + b2) 2 2 1 1 2 1 2 2 1 1 1 5 1 2 1 x x x 2 x 1 x 2 x 1 x 2 2 2 2 4 4 4 2 Применима табличная формула интегрирования Решаем интеграл dx arcsin x C  a a x 1  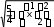  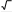 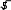 dx dx dx arcsin 2 C arcsin 2x1 C dx dx dx arcsin 2 C arcsin 2x1 C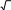 5 52 | |||||||||||
| x 7 4 | 41 |
| 4 | |
| x 7 | 41 |
| 4 4 | |
x
4 16
x
1 ln 2x 2 7x 1 23
1 ln
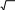
C 1 ln 2x 2 7x 1
4
| 4x 7 | 41 |
| 4x 7 41 | |
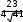 ln
ln 4
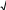
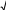 C
C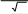
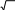 4 8 2 41 4
4 8 2 41 44
Применили в решении табличные формулы интегрирования: dx lnx C ;
x
dx 1 ln xa C
x 2 a 2
2a x a
В итоге решение интеграла имеет вид:
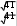 x4 dx 1 ln 2x 2 7x 1 23 ln 4x7 C
x4 dx 1 ln 2x 2 7x 1 23 ln 4x7 C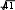 2x 2 7x 1 4 4 4x 7
2x 2 7x 1 4 4 4x 7 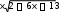 10.8 3x4 dx
10.8 3x4 dxПредставим данный интеграл в виде суммы двух интегралов, предварительно выделив в числителе подынтегральной функции слагаемое, равное производной подкоренного выражения из знаменателя:
2x 4 2 6 6 8 6
3x4 dx 3 3 dx 3 2x6 dx 3 3 dx



 x 2 6x 13 2 x 2 6x 13 2 x 2 6x 13 2 x 2 6x 13
x 2 6x 13 2 x 2 6x 13 2 x 2 6x 13 2 x 2 6x 13 3 2x6 dx 3 10 dx 3 2x6 dx 5 dx
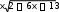
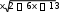
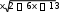
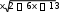 2 2 3 2
2 2 3 2Решение первого интеграла:
3 2x 6
 2 x 2 6x 13
2 x 2 6x 13dx
3 2x 6 x 2
2
1
6x 13 2 dx
3 x 2
2
1
6x 13 2 d x 2
6x 13
3 x 2
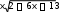 2
2 1 1
6x 13 2
1
С 3
2
x 2
1
6x 13
2
1
С 3 С
1
2 2
Решение второго интеграла
Применима табличная формула интегрирования
dx 1 ln ax C

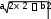 a
a Преобразуем интеграл, выделим в знаменателе подынтегральной функции полный квадрат (формула квадрата суммы (a + b)2 = a2 + 2ab + b2)
x2 6x 13 x2 2 3x 32 32 13 x2 2 3x 9 9 13 x 32 4
Тогда решим интеграл
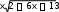

 5dx 5dx 5dx 5ln x 3
5dx 5dx 5dx 5ln x 3  С
С  5ln x 3 С
5ln x 3 СТогда общее решение исходного интеграла:
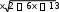
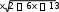
 3x4 dx 3
3x4 dx 3 5ln x 3 C