Справочный материал. 6 класс спрапвочный. Признаки делимости
 Скачать 487.15 Kb.
|
|
Зачёт по математике класс Признаки делимости
Простое число – число, у которого имеются два делителя (единица и оно само) Составное число – число, у которого больше двух делителей. Сократить дробь, значит разделить числитель и знаменатель на одно и тоже число. Чтобы умножить дроби, нужно 1. Посмотреть, можем ли мы что-то сократить, 2. Умножить числитель на числитель, знаменатель на знаменатель. Чтобы найти дробь (часть) от числа, необходимо умножить дробь(часть) на число. Взаимно обратные числа – числа, произведение которых равно единице. Чтобы поделить две дроби, необходимо 1. Нужно первую дробь оставить, 2. Деление заменить умножением, 3. Вторую дробь перевернуть, 4. Посмотреть можем ли мы что-то сократить, 5. Умножить числитель на числитель, знаменатель на знаменатель. Отношение – это частное(деление) двух чисел. Пропорция – это равенство (=) двух отношений. Две переменные прямо пропорциональны – когда при увеличении(уменьшении) одной из них в несколько раз другая увеличивается(уменьшается) во столько же раз. Две переменные обратно пропорциональны – когда при увеличении(уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. Окружность – геометрическая фигура, состоящая из множества точек, находящихся на одинаковом расстоянии от центра. Радиус – отрезок, соединяющий центр окружности с любой точкой на окружности. Диаметр – отрезок, соединяющий две точки на окружности, проходящий через центр. Связь радиуса и диаметра – диаметр равен двум радиусам. Хорда – отрезок, соединяющий две точки на окружности, не проходящий через центр. Длина окружности – 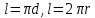 Круг – это плоскость, ограниченная окружностью. Площадь круга –  Целые числа (обозначается буквой Z) – натуральные числа, противоположные им числа и нуль. Натуральные числа (обозначается буквой N) – числа, которые мы используем при счёте. Любое отрицательное число меньше любого положительного числа. Из двух отрицательных чисел меньше то, модуль которого больше. Нуль больше любого отрицательного числа, но меньше любого положительного. Чтобы сложить два отрицательных числа, нужно 1) сложить их модули, 2) поставить перед полученным числом знак «—» Чтобы сложить два числа с разными знаками, нужно 1) из большего модуля слагаемых вычесть меньший, 2) поставить перед полученным числом знак того слагаемого, модуль которого больше. Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + (– b) Например, –18 –14 = –18 + (–14)
Противоположные числа - два числа, отличающиеся друг от друга только знаками. Координатная прямая – прямая с выбранными на ней началом отсчёта, единичным отрезком и направлением. Число, показывающее положение точки на прямой, называют координатой этой точки. Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. Рациональные числа (обозначается буквой Q) – числа, которые можно записать в виде отношения 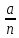 , где a – целое число, а n – натуральное число.Свойства действий с рациональными числами: Переместительный: a + b = b + a Сочетательный: a + (b + c) = (a + b) + c Распределительный: (a + b) · c = a · c + b · c Прибавление нуля: a + 0 = a Умножение на нуль: a · 0 = 0 Умножение на 1: a · 1 = a Модуль числа а – расстояние от начала координат до точки А (а). Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.    Две непересекающиеся прямые на плоскости называют параллельными. Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны. Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой. Система координат на плоскости – это две перпендикулярные координатные прямые x и y, которые пересекаются в начале отсчёта – точке О. Координатная плоскость – плоскость, на которой выбрана система координат. Начало координат – точка О. Прямая х – ось абсцисс. Прямая у – ось ординат.  Пусть М – некоторая точка координатной плоскости. Проведем через неё прямую МА, перпендикулярную координатной прямой х, и прямую МВ, перпендикулярную координатной прямой у. Точка А имеет координату 6, а В – координату -5, тогда точка М определяется парой чисел (6, -5). Эта пара чисел называется координаты точки М.Произведение может быть равно нулю тогда, когда один из множителей равен нуль. a · b = 0, a = 0 или b=0 Чтобы раскрыть скобки, перед которыми стоит знак « ̶ », нужно оставить знак перед скобками, а в скобках заменить знаки на противоположные. Если выражение является произведение числа и одной/несколько букв, то это число называют коэффициентом. Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми. Чтобы сложить подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную часть. Корни уравнения не изменяются, если 1) обе части уравнения умножить или разделить на одно и то же число, не равное нулю, 2) какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. |