Вычисленияе и преобразование. Задания 9 тождественные преобразования выражений числа
 Скачать 92.9 Kb. Скачать 92.9 Kb.
|
|
ЗАДАНИЯ 9: ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ Числа Сложение и вычитание дробей. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть две дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений. Чтобы сложить или вычесть две дроби с разными знаменателями, необходимо сначала привести дроби к общему знаменателю. Умножение дробей. Чтобы умножить две дроби, надо перемножить их числители, перемножить их знаменатели, и разделить первое произведение на второе. Деление дробей. Чтобы разделить дробь на дробь, надо умножить первую дробь на дробь, обратную второй. Возведение дроби в степень. Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель, и разделить степень числителя на степень знаменателя. Формулы сокращенного умножения: 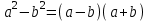 , , 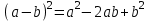 , , 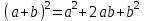 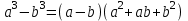 , , 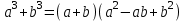 . .Степень. Пусть дано положительное число а и произвольное действительное число n. Число аn называется степенью, число а - основанием степени, число n - показателем степени. Напомним, что по определению полагают: a1 = a, a0 = 1, 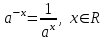 . .Степень с дробным показателем. Если a - положительное число, m - целое число, а n - натуральное число и n ≥ 2, то 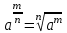 . .В частности, например, 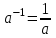 , , 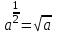 , , 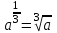 , , 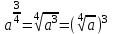 . .Свойства степени. Если a и b - положительные числа, x и y - любые действительные числа, то справедливы следующие свойства: 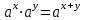 , , 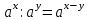 , ,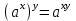 , ,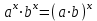 , ,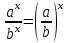 . .Арифметический корень. Пусть n — натуральное число, отличное от единицы, а - неотрицательное число. Арифметическим корнем n-й степени из неотрицательного числа а называется неотрицательное число, n-я степень которого равна а. Для арифметического корня n-й степени из неотрицательного числа а используется обозначение 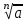 . Если n = 2, пишут . Если n = 2, пишут 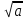 . . По определению 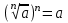 . . Для любых, в том числе отрицательных, значений а справедлива формула 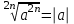 , ,в частности, 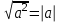 , , 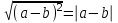 . .Свойства арифметического корня. Если a и b - неотрицательные числа, n и k - натуральные числа, отличные от единицы, m - целое число, то имеют место следующие соотношения: 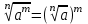 , , 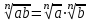 , ,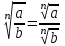 , b ≠ 0, , b ≠ 0,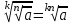 , ,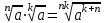 , ,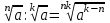 . .Степень с дробным показателем. Если a - положительное число, m - целое число, а n - натуральное число и n ≥ 2, то 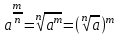 . .Определение логарифма. Логарифмом положительного числа b по основанию а (a > 0, a ≠ 1) называют показатель степени, в которую нужно возвести число а, чтобы получить число b. Для логарифма положительного числа b по основанию а (a > 0, a ≠ 1) используется обозначение logab. По определению 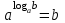 - основное логарифмическое тождество. - основное логарифмическое тождество.Частные случаи: 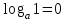 , , 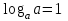 , , 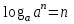 . .Логарифм положительного числа b по основанию 10 называется десятичным логарифмом и обозначается lgb. Логарифм положительного числа b по основанию е называется натуральным логарифмом и обозначается lnb. Свойства логарифмов. Если a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1, x > 0, y > 0, m ≠ 0, n - любое действительное число, то справедливы следующие свойства: 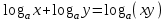 , , 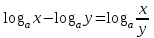 , ,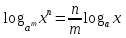 , , 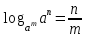 , ,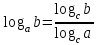 , ,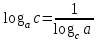 , ,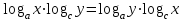 . .Основные тригонометрические формулы 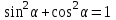 , , 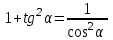 , , 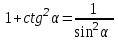 . .Формулы сложения: 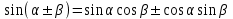 , ,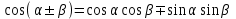 , ,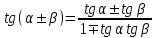 . .Формулы двойного угла: 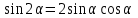 , ,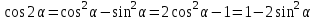 , ,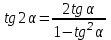 . .Большая часть заданий экзаменационных заданий на преобразования логарифмических выражений представляет собой задачи на вычисление логарифмов; задания на преобразования буквенных логарифмических выражений представлены всего тремя прототипами. При подготовке следует обратить особое внимание на формулу перехода к новому основанию логарифма и следствия из нее: задачи на использование этих формул в школьных учебниках практически не встречаются. Большая часть заданий по тригонометрии представляет собой задачи на вычисление значений числовых тригонометрических выражений с применением формул двойных углов и формул приведения. При этом наиболее часто используются следующие следствия из формул приведения: если α + β = 90°, то , sinα = cosβ, tgα = ctgβ, а если α + β = 180°, то синусы углов α и β равны, а их косинусы, тангенсы и котангенсы противоположны. |
