Главная страница
Навигация по странице:

  • Функция

    		•

    Елизавета№5,6. Накопленная частота, S


    Скачать 69.14 Kb.
    НазваниеНакопленная частота, S
    Дата06.12.2022
    Размер69.14 Kb.
    Формат файлаdocx
    Имя файлаЕлизавета№5,6.docx
    ТипДокументы
    #831859

    №5.

    xi
    Кол-во, ni
    xi·ni
    Накопленная частота, S
    |x-xср|·ni
    (x-xср)2·ni
    Относительная частота, ni/n

    14
    3
    42
    3
    104.428
    3635.051
    0.0173

    17
    14
    238
    17
    445.329
    14165.596
    0.0809

    20
    28
    560
    45
    806.659
    23239.238
    0.162

    22
    32
    704
    77
    857.896
    22999.546
    0.185

    54
    44
    2376
    121
    228.393
    1185.532
    0.254

    87
    52
    4524
    173
    1985.919
    75843.742
    0.301

    Итого
    173
    8444



    4428.624
    141068.705
    1


    Средняя взвешенная (выборочная средняя)


    Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑n/2 = 87. Это значение xi = 54.

    Дисперсия:

    Несмещенная оценка дисперсии:

    Среднее квадратическое отклонение.


    Функция распределения F(X).
    F(x≤14) = 0
    F(14< x ≤17) = 0.0173
    F(17< x ≤20) = 0.0809 + 0.0173 = 0.0982
    F(20< x ≤22) = 0.16 + 0.0982 = 0.258
    F(22< x ≤54) = 0.18 + 0.258 = 0.438
    F(54< x ≤87) = 0.25 + 0.438 = 0.688
    F(x>87) = 1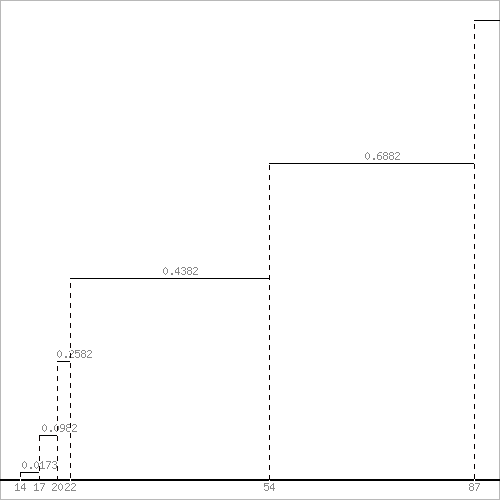


    №6.

    X / Y
    7
    8
    9

    200
    41
    7
    0

    300
    1
    52
    1

    400
    0
    8
    40




    X
    200
    300
    400



    P
    0.32
    0.36
    0.32
    ∑Pi = 1


    Математическое ожидание M[X].
    M[x] = 200*0.32 + 300*0.36 + 400*0.32 = 300
    Дисперсия D[X].
    D[X] = 2002*0.32 + 3002*0.36 + 4002*0.32 - 3002 = 6400
    Среднее квадратическое отклонение σ(x).


    Y
    7
    8
    9



    P
    0.28
    0.4467
    0.2733
    ∑Pi = 1


    Математическое ожидание M[Y].
    M[y] = 7*0.28 + 8*0.45 + 9*0.27 = 7.99
    Дисперсия D[Y].
    D[Y] = 72*0.28 + 82*0.45 + 92*0.27 - 7.992 = 0.55
    Среднее квадратическое отклонение σ(y).


    cov(X,Y) = M[X*Y] - M[X]*M[Y]
    cov(X,Y) = 7*200*0.2733 + 8*200*0.04667 + 7*300*0.00667 + 8*300*0.3467 + 9*300*0.00667 + 8*400*0.05333 + 9*400*0.2667 - 300*7.99 = 54

    Коэффициент корреляции.






    tкрит (n-m-1;α/2) = (148;0.025) = 2.263

    Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

    Запишем уравнения линий регрессии y(x):

    и вычисляя, получаем:
    yx = 97.6 x - 480.13

    написать администратору сайта