КР_МК. Направлении L
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
Проверки местной устойчивостиПроверка местной устойчивости сжатого поясаПо п. 8.5.18 [1] местная устойчивость сжатого пояса обеспечена, если условная гибкость свеса пояса 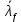 не превышается предельного значения не превышается предельного значения 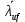 : :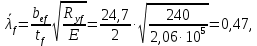 где bef – величина неокаймленного свеса, равная 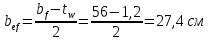 Предельное значение условной гибкости свеса полки двутаврового сечения определяем по формуле 97 [1]: 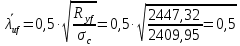 где 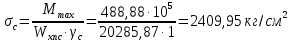 Условие выполнено, следовательно, устойчивость сжатого пояса обеспечена. Проверка местной устойчивости стенкиРасстановка ребер жесткости. Предусматриваем парные поперечные (вертикальные) ребра в местах опирания ба лок настила и на опорах (рис. 9). Согласно п. 8.5.9. [1], при w 4, 44 3, 2 расстояние а между ребрами жесткости не должно превышать 2hef= 310 см > a= 210 см. 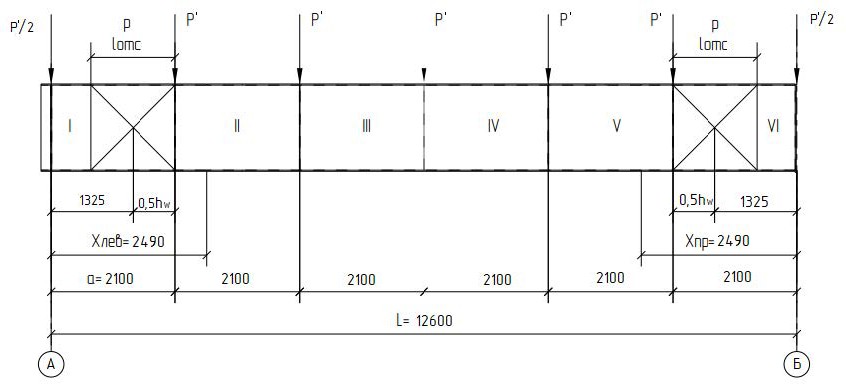 Рис. 9. Схема расстановки ребер жесткости по длине балки Б2 Определение размеров промежуточных ребер Требуемая ширина по п.8.5.9 [1]: 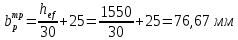 Принимаем bp=80 мм  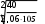 Требуемая толщина ребра: Требуемая толщина ребра:  р р tтр 2b 2 80 5,46 мм Принимаем tр = 6 мм, тогда bр×tр= 80×6 мм. При сопряжении балок в одном уровне из условия размещения болтов минимальные размеры ребра 110×10 мм. Окончательно принимаем bр×tр= 110×10 мм. 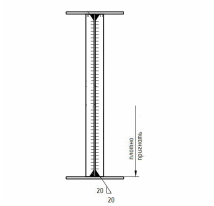 Рис. 10 Промежуточное ребро жесткости: а – при этажном сопряжении балок Б1 и Б2; б – при сопряжении в одном уровне Проверка местной устойчивости стенки При w 4, 44 3, 5 согласно п. 8.5.1. [1], необходимо проводить проверку местной устойчивости стенки. Выполняем проверку местной устойчивости по формуле 80 [1]: 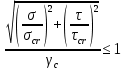 где γc= 1 (табл.1 [1]); напряжение σ и τ следует вычислять по формулам 78 и 79 [1] соответственно: Q twhw   I ' M 0, 5hw x или M 0, 5hw, Ix   l . р отс где Q и М – среднее значение поперечной силы и момента на расчетной длине отсека При a/hef>1 принимаем lотсp=hef=155 cм  σcrвычисляется в соответствии с формулой 81 [1]: cr ccr Ry   2 w 30 2447,32 3724,31 кг/ см2 4,442 где ccr– коэффициент, определяемый в соответствии с п. 8.5.4. по табл.12 [1] и принимаемый с запасом в учебных целях равным 30. τcrвычисляется в соответствии с формулой 83 [1]: 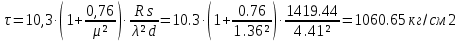 где μ– отношение большей стороны отсека стенки к меньшей: μ=a/hes=210/155=1,36. d– меньшая из сторон отсека по стенке (aили hef), то есть d= hef= 155 см; 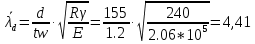 проверка устойчивости в I-ом отсеке Так как в I-ом отсеке сечение балки постоянно и момент инерции равен Ix, то M и Qдолжны быть вычислены на расстоянии 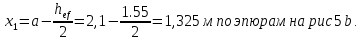 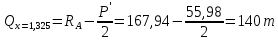 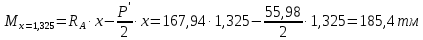 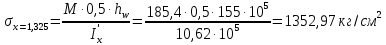 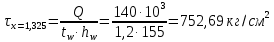 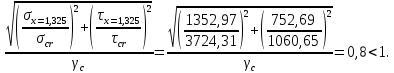 Местная устойчивость стенки в I-ом отсеке обеспечена. В силу симметрии задачи устойчивость в VI отсеке также обеспечена. При несимметричном загружении главной балки устойчивость стенки необходимо проверять и в крайних отсеках справа. проверка устойчивости в II-ом отсеке (см. рис. 11) 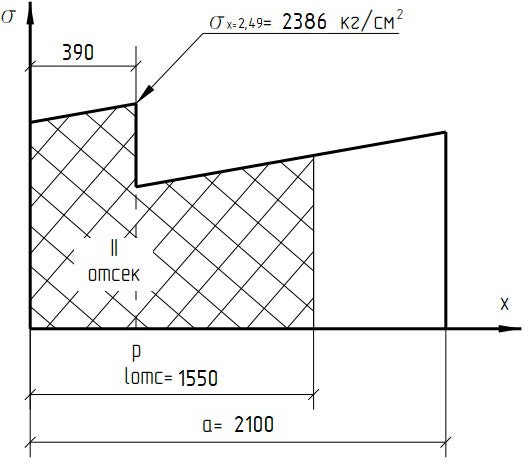 Рис. 11 Схема II-го отсека Так во II отсеке сечение балки меняется и момент инерции равен 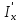 , то x2= 2,49 м. , то x2= 2,49 м. 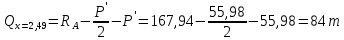 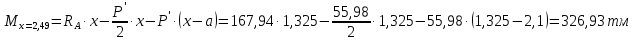 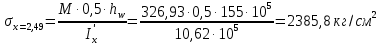 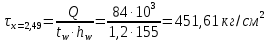 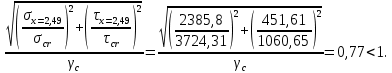 Местная устойчивость стенки в II-ом отсеке обеспечена. В силу симметрии задачи устойчивость в V отсеке также обеспечена. проверка устойчивости в III-ем отсеке Устойчивость в этом отсеке будет обеспечена, т.к. значение σ будет близким к значению σ во II отсеке, а τ будет меньше, при этом в III-ем отсеке будет использован момент инерции основного сечения. В силу симметрии задачи устойчивость в IV отсеке также обеспечена. |
