НАРАЩЕНИЕ И ДИСКОНТИРОВАНИЕ ПО ПРОСТЫМ И СЛОЖНЫМ ПРОЦЕНТАМ. Наращение и дисконтирование по простым и сложным процентам
 Скачать 67.56 Kb. Скачать 67.56 Kb.
|
 НАРАЩЕНИЕ И ДИСКОНТИРОВАНИЕ ПО ПРОСТЫМ И СЛОЖНЫМ ПРОЦЕНТАМ Вариант 5 Задача 1. Определить проценты и сумму накопленного долга, если ссуда равна 700 тыс.руб., срок 3 года, проценты простые по ставке 20% годовых. Размер ссуды, тыс.руб.:600 Срок начисления, год :3 Процентная ставка, % :18 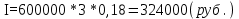 - проценты за 3 года - проценты за 3 года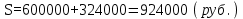 - наращенная сумма. - наращенная сумма.Задача 2 Кредит в размере 3 млн.руб. выдан на 3 года и 160 дней под 16,5% сложных годовых. Найти сумму долга на конец срока общим и смешанным способами. Сравнить полученные результаты. 2 года и 190 дней 18,5% Решение. n = 2+ 190/365 = 2.5205 1. Общий метод 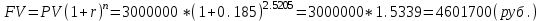 2. Смешанный метод 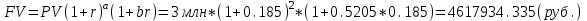 Вывод. Смешанный метод дает больший результат. Задача 3. Ссуда в размере 25 тыс. руб. выдана С 10.01 до 25.12 под 6,5% годовых (простая процентная ставка). Определить размер погашаемой суммы тремя способами: 1) «Точные проценты с точным числом дней ссуды» 2) «Обыкновенные проценты с точным числом дней ссуды» 3) «Обыкновенные проценты с приближенным числом дней ссуды» Возможные варианты расчета наращенной суммы: 1) по точным процентам с точным числом дней ссуды: 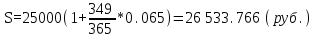 2) по обыкновенным процентам с точным числом дней ссуды: 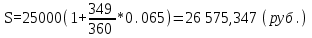 3) по обыкновенным процентам с приближенным числом дней ссуды: 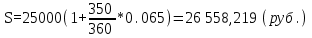 Задача 4. Долговое обязательство на сумму 4 млн. руб., срок которого наступает через 8 лет, продано с дисконтом по сложной учетной ставке 15% годовых. Каков размер полученной за долг суммы и величина дисконта (в тыс. руб.)? Решение. 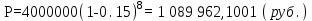 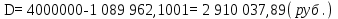 Задача 5. Какой величины достигнет долг, равный 1000 тыс.руб., через 4 лет при сложной процентной ставке 14,5 % годовых, если начисление процентов происходит полугодовое раза в год? Решение. Все расчеты проводим по формуле 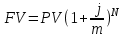 . .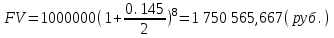 Задача 6. Ссуда в размере 20тыс.руб выдана на 2 года. Проценты начисляются в конце каждого квартала по номинальной ставке сложных процентов, равной 30% годовых.. Определить погашаемую сумму. 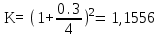 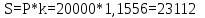 Задача 7. Через 190 дней после подписания договора должник уплатит 700 тыс. руб. Кредит выдан под 18% годовых. Какова первоначальная сумма долга при условии, что временная база равна 360 дням? 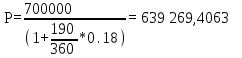 Задача 8. Ссуда в размере 700 тыс. руб. выдана 1 марта до 5 сентября под 18 % годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить метод «Обыкновенные проценты с приближенным числом дней ссуды». 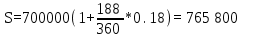 Задача 9. Переводной вексель выдан на сумму 900 тыс.руб. с уплатой 14 декабря. Владелец учел его в банке 1 ноября по учетной ставке 16 % (365/360). Чему равна полученная при учете сумма? Чему равна величина дисконта? 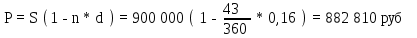 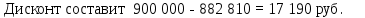 Задача 10. Контракт предусматривает следующий порядок начисления процентов: первый год – 19 %, следующие два полугодия – ставка повышается на 2 %; в каждом последующем квартале – ставка повышается еще на 1 %. Необходимо определить множитель наращения за 3 года. 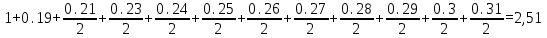 Задача 11. Ссуда равна 800 тыс.руб., срок 4 года, проценты простые по ставке 10 % годовых. Во сколько раз увеличится наращенная сумма, если процентная ставка увеличится в полтора раза? 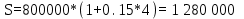 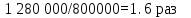 Задача 12. Кредит в размере 700 тыс. руб. выдан на 2 года. Реальная доходность операции должна составлять 10 % годовых по сложной ставке процентов. Ожидаемый уровень инфляции составляет 14 % в год. Определить множитель наращения, учитывающий инфляцию и наращенную сумму. 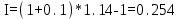 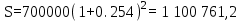 сложная ставка процентов равна 25.4%, множитель наращения – 1,572516 наращенная сумма – 1 100 761,2 тыс. руб Лаба 2 Задача 1. Сравнить на начало осуществления проекта два варианта инвестиций (А и Б), если ставка дисконтирования равна 11 %, используя все три показателя эффективности капитальных вложений (ЧДД, ИР, ДСО).
Решение: Для того, чтобы рассчитать дисконтированный срок окупаемости и чистый дисконтированный доход, обеспечив при этом сопоставимость показателей, приведем к начальному моменту времени (продисконтируем) капитальные затраты и поступления по данному проекту. Приведенная к текущему моменту (дисконтированная) стоимость будущих поступлений рассчитывается по следующей формуле: 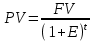 , ,где PV – первоначальная (приведенная) стоимость. FV – будущая стоимость. E – ставка банковского процента. t – количество лет или оборотов капитала. Чистый дисконтированный доход (NPV) – приведенная стоимость будущих прибылей или денежных потоков, дисконтированных с помощью соответствующей процентной ставки за вычетом приведенной стоимости инвестиционных затрат. Чистый дисконтируемый доход (NPV) рассчитывается по следующей формуле: NPV = Сумма дисконтированных доходов – Сумма дисконтированных затрат По исходным данным ставка дисконтирования – 11%. Представим рассчитанные показатели дисконтированных (приведенных к начальному моменту времени) затрат и поступлений по указанным инвестиционным проектам в следующей таблице:
Следовательно, чистый дисконтированный доход (NPV) инвестиционного проекта А составляет 84,36 Чистый дисконтированный доход (NPV) инвестиционного проекта B составляет 87,93 Таким образом, исходя из показателя чистого дисконтированного дохода (NPV), наибольшую экономическую эффективность имеет проект B (87,93 > 84,36.). Дисконтированный срок окупаемости инвестиционного проекта А составит 5 года (т.к. сумма дисконтированных доходов нарастающим итогом превысит величину первоначальных инвестиций только через 5 лет = -189,18 +113,62 + 109,67+ 79,04+71,21= 184,36 > 100). Дисконтированный срок окупаемости инвестиционного проекта B составит 6 лет (т.к. сумма дисконтированных доходов нарастающим итогом превысит величину первоначальных инвестиций только через 6 лет = -45,04+ 73,04+ 102,36+ 52,69+59,34+85,54= 327,93 > 240). Задача 2. Ваше предприятие предполагает построить офис. Примерная смета приведена ниже: 1) 900 000 руб. необходимо оплатить сразу и дополнительно оплатить покупку земли в размере 130 000 руб. 2) 100000 руб. оплатить через год Через два года после строительства офис будет по Вашим оценкам стоить 1 510 000 руб. Целесообразно ли начинать строительство офиса, если банковская процентная ставка по годичным вкладам составляет 11% годовых? Вывод сделать, опираясь на величину чистого дисконтированного дохода.
Решение: Для того, чтобы рассчитать дисконтированный срок окупаемости и чистый дисконтированный доход, обеспечив при этом сопоставимость показателей, приведем к начальному моменту времени 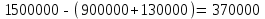 Приведенная к текущему моменту (дисконтированная) стоимость будущих поступлений рассчитывается по следующей формуле: 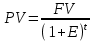 , ,где PV – первоначальная (приведенная) стоимость. FV – будущая стоимость. E – ставка банковского процента. t – количество лет или оборотов капитала. Чистый дисконтированный доход (NPV) – приведенная стоимость будущих прибылей или денежных потоков, дисконтированных с помощью соответствующей процентной ставки за вычетом приведенной стоимости инвестиционных затрат. Чистый дисконтируемый доход (NPV) рассчитывается по следующей формуле: NPV = Сумма дисконтированных доходов – Сумма дисконтированных затрат Предпочтение отдается проектам, у которых NPV > 1. По исходным данным ставка дисконтирования – 11%. Представим рассчитанные показатели дисконтированных (приведенных к начальному моменту времени) затрат и поступлений по указанным инвестиционным проектам в следующей таблице:
Вывод: Следовательно, чистый дисконтированный доход (NPV) составляет 1 009 090,16 руб. Сумма дисконтированных доходов нарастающим итогом превысит величину первоначальных инвестиций через 2 года = 927 927,92 + 81 162,24=1 009 090,16 руб. > 370 000 руб.). Т.е. целесообразно начинать строительство офиса, если банковская процентная ставка по годичным вкладам составляет 11% годовых. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
