огэ задания. ОГЭ задания. Населённые пункты
 Скачать 0.57 Mb.
|
|
Вариант № 1 1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
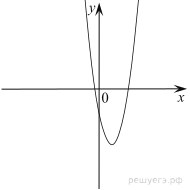
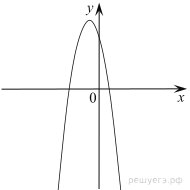
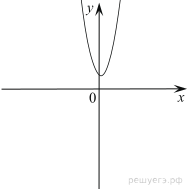
Марина летом отдыхает у дедушки в деревне Ивановки. В пятницу они собираются съездить на машине в село Гавриловка. Из Ивановки в Гавриловку можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Пересыпкино до деревни Ольшанка, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Гавриловку. Есть и третий маршрут: в Пересыпкине можно свернуть на прямую грунтовую дорогу, которая идёт мимо пруда прямо в Гавриловку. П 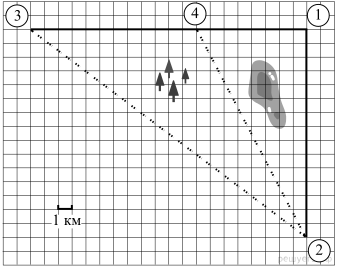 о шоссе Марина с дедушкой едут со скоростью 48 км/ч, а по грунтовой дороге — 25 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 1 км.2. Найдите расстояние от деревни Ивановки до села Гавриловка по прямой. Ответ выразите в километрах. 3. Сколько километров проедут Марина с дедушкой, если они поедут по шоссе через деревню Ольшанку? 4. Сколько времени затратят на дорогу Марина с дедушкой, если они поедут сначала до Пересыпкино, а затем свернут на грунтовую дорогу, идущую мимо пруда? Ответ выразите в минутах. 5. Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Марина с дедушкой, если поедут этим маршрутом. 6. Найдите значение выражения  7. На координатной прямой отмечены числа p, q и r.  Какая из разностей q − p, q − r, r − p отрицательна? В ответе укажите номер правильного варианта. 1) q – p; 2) q – r; 3) r – p; 4) ни одна из них 8. Найдите значение выражения  В ответе укажите номер правильного варианта. 1) 5; 2)  ; 3)  ; 4) 409. Решите уравнение (−5x + 3)(−x + 6) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней. 10. Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием учебного года, из них 8 с машинами и 12 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Вася. Найдите вероятность того, что Васе достанется пазл с машиной. 11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c. КОЭФФИЦИЕНТЫ А)  ; Б)  ; В)  ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер. 12. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6500 + 4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ дайте в рублях. 13. На каком рисунке изображено множество решений неравенства  В ответе укажите номер правильного варианта. 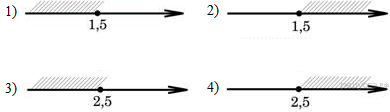 1 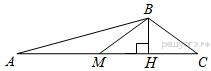 4. Мощности пяти различных электромоторов составляют возрастающую геометрическую прогрессию. Мощность самого слабого электромотора — 5 кВт, а третьего по мощности — 20 кВт. Найдите мощность самого мощного электромотора, ответ дайте в кВт.15. В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах. 16. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 1, AC = 5. 1 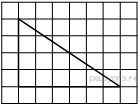 7. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.18. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета. 19. Какие из данных утверждений верны? Запишите их номера. 1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2) Площадь круга меньше квадрата длины его диаметра. 3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб. 20. Решите неравенство  21. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 6 км/ч пешехода за 8 секунд. Найдите длину поезда в метрах. 22. ЗПостройте график функции  Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки. 23. Стороны AC, AB, BC треугольника ABC равны  ,  и 1 соответственно. Точка K расположена вне треугольника ABC , причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90°.24. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник. 25. Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 16. Вариант № 2 1. Игорь страховал свою гражданскую ответственность три года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Игорю на начало четвёртого года страхования? Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.
2. Чему равен КБМ на начало четвёртого года страхования? 3. Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу). К 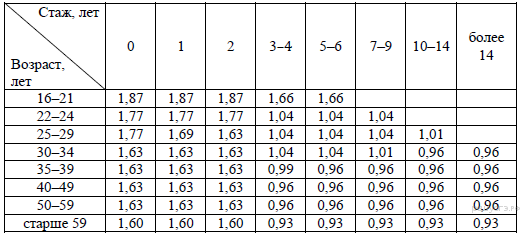 огда Игорь получил водительские права и впервые оформил полис, ему было 22 года. Чему равен КВС на начало 4-го года страхования?4. В начале третьего года страхования Игорь заплатил за полис 18 585 руб. Во сколько рублей обойдётся Игорю полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся? 5. Игорь въехал на участок дороги протяжённостью 2,6 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге — 100 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Игорь въехал на участок в 11:10:33, а покинул его в 11:11:51. Нарушил ли Игорь скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой? 6. Найдите значение выражения  7. На координатной прямой отмечены числа x и y.  Какое из приведенных утверждений для этих чисел неверно?
8. Найдите значение выражения  9. Решите уравнение −2(5 − 3x) = 7x + 3. 10. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков. 11. Установите соответствие между графиками функций и формулами, которые их задают. Графики
Формулы
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: 12. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам. 13. Решение какого из данных неравенств изображено на рисунке? В ответе укажите номер правильного варианта. 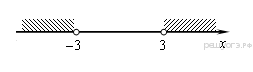 1)  ; 2)  ; 3)  ; 4)  14. Пете надо решить 333 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Петя решил 5 задач. Определите, сколько задач решил Петя в последний день, если со всеми задачами он справился за 9 дней. 1 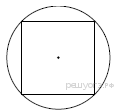 5. О снования равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.16. Радиус окружности, описанной около квадрата, равен  Найдите длину стороны этого квадрата.1  7. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.18. На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь. 19. Какое из следующих утверждений верно? 1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. 2) В любой прямоугольник можно вписать окружность. 3) Каждая из биссектрис равнобедренного треугольника является его медианой. В ответе запишите номер выбранного утверждения. 20. Решите систему уравнений 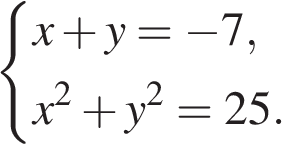 21. Из пунктов А и В, расстояние между которыми 27 км, вышли одновременно навстречу друг другу два туриста и встретились в 12 км от В. Турист, шедший из А, сделал в пути получасовую остановку. Найдите скорость туриста, шедшего из В, если известно, что он шёл со скоростью, на 2 км/ч меньшей, чем первый турист. 22. Постройте график функции  Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек. 2  3. Стороны AC, AB, BC треугольника ABC равны  ,  и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90° .24. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный. 25. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC. Вариант № 3 1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Н 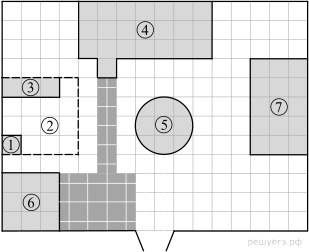 а плане изображено домохозяйство по адресу: с. Корнеево, улица Парковая, д. 3 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.При входе на участок слева от ворот находится веранда, отмеченная на плане цифрой 6. Площадь, занятая верандой, равна 9 кв. м. Жилой дом находится в глубине территории. Помимо веранды и жилого дома, на участке имеются будка, имеющая наименьшую площадь на участке, и теплица, построенные на территории огорода (огород отмечен цифрой 2). Также в центре участка перед домом расположен пруд, а справа от него гараж. Все дорожки внутри участка вымощены тротуарной плиткой размером 0,5 м × 0,5 м. Перед верандой имеется площадка, вымощенная такой же плиткой. На участке планируется провести электричество. 2. Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобится, чтобы выложить все дорожки и площадку перед верандой? 3. Найдите площадь огорода (в м2), не занятую постройками. 4. Найдите расстояние от жилого дома до будки (расстояние между двумя ближайшими точками по прямой) в метрах. 5. Хозяин участка планирует провести на участок электричество. Он рассматривает два варианта: купить генератор или продлить до своего дома линию электропередач. Данные о расходе топлива (электроэнергии) и стоимости ценах указаны в таблице.
Обдумав оба варианта, хозяин решил купить генератор. Через сколько часов непрерывного использования электроэнергии экономия от использования генератора вместо линии электропередач компенсирует разность в стоимости организации электричества на участке? 6. Найдите значение выражения  7. Одно из чисел  отмечено на прямой точкой. Укажите это число. В ответе укажите номер правильного варианта.
8. Найдите значение выражения  9. Найдите корень уравнения  10. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России. 11.На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций. Графики 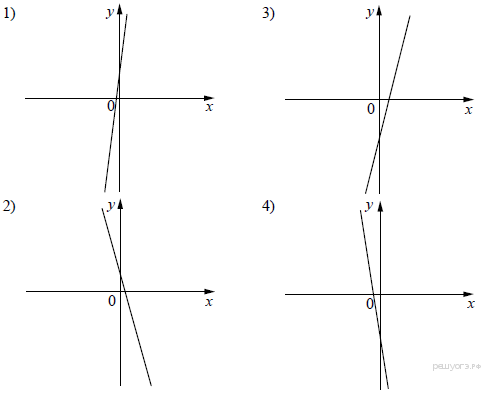 Коэффициенты
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых. 13. Решите неравенство  и определите, на каком рисунке изображено множество его решений.В ответе укажите номер правильного варианта. 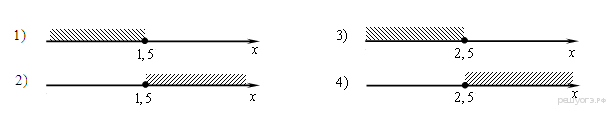 14.Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день? 1  5. Тангенс острого угла прямоугольной трапеции равен  Найдите её большее основание, если меньшее основание равно высоте и равно 7.1  6. Радиус окружности, описанной около квадрата, равен  Найдите длину стороны этого квадрата.17. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π. 18. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета. 19. Какие из следующих утверждений верны? 1) Все диаметры окружности равны между собой. 2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. 3) Любые два равносторонних треугольника подобны. В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов. 20. Решите систему неравенств 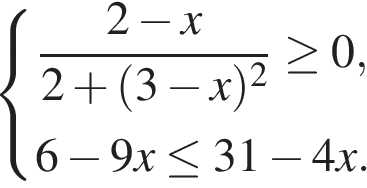 21. При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли, концентрация которого 48%, получился раствор с концентрацией 42%. В каком отношении были взяты первый и второй растворы? 22. Известно, что парабола проходит через точку  и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую  23. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 14, DC = 56, AC = 40 . 24. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников AEB и CED равна половине площади параллелограмма. 25. Окружности радиусов 12 и 20 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD. Вариант № 4 1. Установите соответствие между объёмами помещения и номерами печей, для которых данный объём является наименьшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проёма 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трёх печей.
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6500 руб. 2. Найдите объём парного отделения строящейся бани. Ответ дайте в кубических метрах. 3. Во сколько рублей обойдётся покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей? 4. На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь? 5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи показан на рисунке 2. 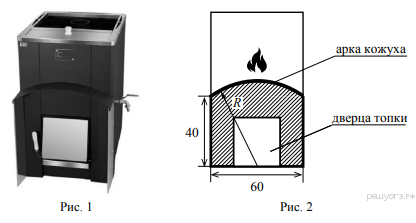 Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах. 6. Запишите в ответе номера тех выражений, значение которых равно −5. Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
7. На координатной прямой отмечено число a.  Найдите наибольшее из чисел a2, a3, a4. В ответе укажите номер правильного варианта. 1) a2 2) a3 3) a4 4) не хватает данных для ответа 8. Найдите значение выражения  9. Решите уравнение  10. Известно, что в некотором регионе вероятность того, что родившийся младенец окажется девочкой, равна 0,488. В 2010 г. в этом регионе на 1000 родившихся младенцев в среднем пришлось 532 мальчика. Насколько частота рождения мальчика в 2010 г. в этом регионе отличается от вероятности этого события? 11. Установите соответствие между функциями и их графиками. ФУНКЦИИ А)  Б)  B)  ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует −1° по шкале Цельсия? 13. Решите неравенство  и определите, на каком рисунке изображено множество его решений.В ответе укажите номер правильного варианта. 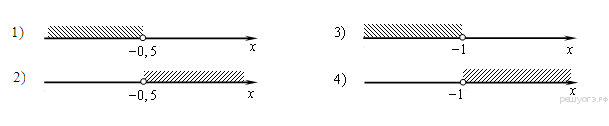 14. Часть программы тренировок Арсения заключается в беге на беговой дорожке. На первой тренировке необходимо бежать 15 минут, на каждой следующей время пробежки увеличивается на 7 минут. За сколько тренировок Арсений проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать программе? (В ответе укажите только число.) 1   5. Точки  и  являются серединами сторон  и  треугольника  , сторона равна 48, сторона равна 57, сторона  равна 72. Найдите  16. Окружность с центром в точке  описана около равнобедренного треугольника , в котором  и  . Найдите угол  . Ответ дайте в градусах.1  7. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 11 и 14. Найдите длину основания BC.1  8. На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.19. Какое из следующих утверждений верно? 1. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. 2. Все углы ромба равны. 3. Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом. В ответ запишите номер выбранного утверждения. 20. Решите неравенство  21. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий? 22. Постройте график функции  Определите, при каких значениях  прямая  имеет с графиком ровно три общие точки.2  3. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 6, а сторона AC в 1,5 раза больше стороны BC.24. В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб. 25. Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
