для хади работа. Научноисследовательская работа по математике Математика в школе. Проценты, дроби, доли в кулинарии. Илиева Х. М. 5 класс
 Скачать 1 Mb.
|
|
ГБОУ «Лицей №1 г.Назрань» Научно-исследовательская работа по математике «Математика в школе. Проценты, дроби, доли в кулинарии». Выполнила: Илиева Х.М. 5 класс Руководитель: Мержоева Л.Я., учитель математики 2023г. Содержание Введение………………………………………………………………….…………….3 Теоритическая часть 1.1 Немного истории…………………………………………………...………………5 1.2 Математика в кулинарии ...………………………………………………………..5 1.3 Профессия кондитера и повара……………………………………………………6 1.4 Проценты , дроби и доли в кулинарии…………………………………….………7 1.5 Измерения в кулинарии ………………………………………………..…………13 Практическая часть 2.1 Практическая работа ……………………………………………………………….14 Заключение…………………………………………………………………...………...16 Список литературы……………………………………………………………………17 Введение С древних времен в своей повседневной жизни человек не мог обойтись без счета. У каждого народа необходимость в простейших арифметических подсчетах возникала задолго до появления первых зачатков письменности, потому что постижение Мира во всем его многообразии постоянно требовало количественной оценки обретенных знаний. Используя опыт ушедших поколений, первые великие мыслители своими открытиями закладывали фундамент древнейшей из наук, имя которой – математика. Неслучайно корень этого слова в переводе с греческого означает «наука». Десятки веков канули в прошлое, но до нас дошло овеянное славой имя древнегреческого ученого Пифагора, жившего в середине тысячелетия до нашей эры. "Все есть число" - считал он, и мир чисел жил для Пифагора и его последователей особой жизнью. В копилке мировых знаний не поблекли сокровища, подаренные человечеству Архимедом, великим древнегреческим математиком и механиком, погибшим при защите Сиракуз от римлян за 200 лет до нашей эры. «Дайте мне точку опоры, и я поверну Землю," - говорил Архимед. Многие известные учёные говорят, что главное в математике — научить человека мыслить, ставя порою перед ним очень сложные задания. «Математика развивает логическое мышление, умение самостоятельно решать проблемы, способность быстро уловить суть и найти к жизненной задаче наиболее подходящий и простой подход» - говорят нам взрослые. Математика тесно связана с нашей повседневной жизнью. Она встречается в нашей жизни практически на каждом шагу и не такая уж она серая и скучная, а разноцветная и веселая... Рассмотрим, как математика применяется в кулинарии. Цель исследования: Узнать об использовании процентов, дробей и долей в кулинарии Задачи исследования: Исследовать литературу о математике и кулинарии. Собрать данные и обработать информацию о применении математических знаний о процентах, дробях и долях в кулинарии. Объект исследования: Проценты, дроби и доли в кулинарии. Актуальность: В школе большое внимание уделяется математике. Мне захотелось узнать, как пригодится математика в таких процессах, как кулинария. Проблема: Какую роль играет математика, а в частности проценты, дроби и доли в кулинарии? Гипотеза: Математические знания выручают в различных жизненных ситуациях, математика применяется в кулинарии. С помощью математических знаний, полученных в школе, мы решаем не только арифметические задачи, но и применяем эти знания в различных жизненных ситуациях. Математика служит во благо человеку. Решать головоломки так же увлекательно, как готовить яблочный пирог. А вкус хорошего вина так же многогранен, как сложная математическая структура. Почему между готовкой и математикой много общего? (Джим Хенли) Методы исследования: Изучение литературы по теме. Беседы со специалистами, с родителями. Наблюдения. Практическая работа. Теоретическая часть Немного истории «CULINARIUS» – в Древнем Риме «искусство приготовления пищи» Кулинария высоко ценилась во все времена, но при этом она всегда подчинялась законам капризной моды точно так же, как искусство изготовления одежды, украшений и предметов интерьера. Судьба нации зависит от способа ее питания. (А.Брилья-Саварен. Физиология вкуса) Эта фраза высокопоставленного французского чиновника-юриста, до самозабвения, увлеченного кулинарным искусством, имеет под собою ряд убедительных исторических примеров. Погрязшая в безграничной роскоши, в том числе и стола, Римская империя пала, а исповедовавшая умеренность в еде и простоту пищи Спарта в течение долгого времени давала миру совершенных по своему физическому и нравственному развитию граждан. Как видим, способ питания нации, народа, выражением которого является поваренное искусство, не такой уж второстепенный вопрос и изучение истории питания не такое уж бесполезное дело. Существует множество рецептов блюд, которые названы по имени знаменитых людей, а также в честь поваров, создавших их. К таким блюдам относятся, например, бешамель, сэндвич, салат «Оливье» или вкусное мясное кушанье бефстроганов. Математика используется не только в науке, но и в кулинарии при приготовлении пищи. На самом деле, все этапы приготовления пищи, в том числе покупка продуктов питания, расходы бюджета требуют некоторые математические знания. 1.2 Математика в кулинарии Математика применяется практически во всех областях человеческой деятельности, в разных профессиях. Мы исследовали, как используются математические знания в кулинарии. Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления. При взвешивании продуктов в кулинарии используются математические величины-масса и объём. Ими тоже необходимо уметь пользоваться. Единицы времени играют далеко не последнюю роль в приготовлении блюд. Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика. Ели вы хотите поддерживать себя в хорошей форме, то вам необходимо следить за поглощаемыми калориями. При подсчете калорийности готовых блюд учитываются её изменения при различных видах кулинарной обработки: варка, жарка, тушение, кипячение и др. Учитывается в обязательном порядке потеря белков, жиров, углеводов, витаминов и минералов при обработке и даже при нарезке продуктов. Учитывается потеря массы готового блюда и использование воды при приготовлении. Истинный повар должен обладать хорошей памятью, уметь быстро считать, и знать основные математические понятия: Проценты, дроби, доли. 1.3 Профессия кондитера и повара Актуальность и востребованность поварского дела доказана тысячелетней историей этого искусства. Первые повара появились, как только человек научился не только добывать пищу, но и готовить её. А это произошло далеко не сразу, так как поначалу единственным источником еды было собирательство и охота. А употребляли древние люди еду в сыром виде. Знатные люди в Древнем Риме и в Древней Греции особенно ценили вкусную пищу. Огромный спрос на разнообразие и обилие разных яств привело к образованию первых кулинарных школ. Ведь квалифицированных поваров просто не хватало. В 19 веке поварские школы стали появляться повсеместно. Европа, Англия и Россия на перебой готовили своих специалистов. В древности еще не существовало такого понятия, как профессия, но кондитерское ремесло возникло довольно давно. Точно конечно нельзя сказать, кто же были первыми кондитерами, возможно индейцы племени майя, которые открыли удивительные свойства шоколада, а может быть жители Древней Индии, сумевшие познать вкус тростникового сахара и готовить из него сладкие палочки. Профессия кондитер самая востребованная, вкусная и творческая профессия. Настоящий кондитер – это профессиональный повар, создающий кондитерские изделия, выпечку и десерты. Профессия кондитер очень актуальна, потому что среди продукции пищевой промышленности кондитерские изделия являются одними из самых популярных и востребованных во всем мире, так как они обладают особыми вкусовыми качествами и высокой энергетической ценностью. В европейских странах производители кондитерских изделий должны обладать не только знаниями в области их приготовления, но и умением считать, делать соотношения, рисовать, чертить, лепить и создавать замысловатые геометрические формы. А для этого просто необходимы математические знания. Технология мучных кондитерских изделий – важная специальная дисциплина. На занятиях по этому предмету вы сталкиваетесь с большим количеством математических расчетов. Поэтому математика тоже является важной основой для получения профессиональных знаний. 1.4 Проценты, дроби, доли в кулинарии Когда мы описываем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе. Чтобы называть сотые доли, придумали процент (1/100): с латинского языка — «за сто». Процент — это одна сотая часть от любого числа. Обозначается вот так: %. 1%=1:100=0,01 Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18. А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например: 0,18 = 0,18 · 100% = 18%. А вот, как перевести проценты в десятичную дробь — обратным действием: 18% : 100% = 0,18. Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение. Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.  Посмотрим на этот рисунок. Представим, что это наша пицца, разделённая на четыре куска – доли. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы. Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия: Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:  А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:  Такие записи называют дробями. Дробь состоит из числителя и знаменателя. Число, которое записывается сверху, называется числителем дроби. Число, которое записывается снизу, называется знаменателем дроби. В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы. Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь? Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):  Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли». Теперь представьте, что пиццу мы разделили не на четыре части, а на три.  Допустим мы съели один кусок этой пиццы. Как записать такую дробь? Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:  Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть». Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:  Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:  Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь? Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:  Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина». Дроби, которые мы сейчас рассмотрели, называют обыкновенными. Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже. Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться. На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4. 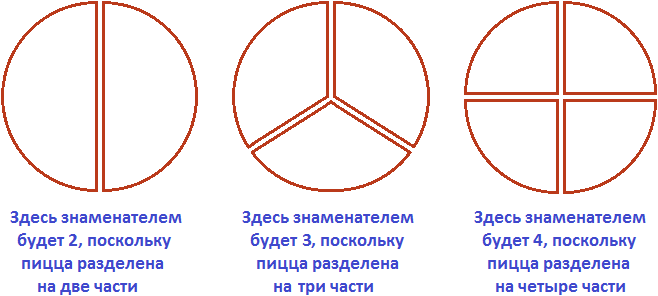 Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли  (одну часть из двух), или как говорят в народе «половину» пиццы.С помощью переменных дробь можно записать так:  где a — это числитель, b — знаменатель.Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными. Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:  Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём  (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными: 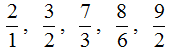 Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.Теперь возьмём к примеру неправильную дробь  и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например: 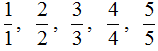 Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь  . Применим её к нашей пицце.Допустим, мы хотим съесть пиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим эту пиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.Дробь означает деление Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель. Например, рассмотрим дробь 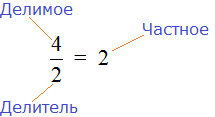 . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ: Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например: 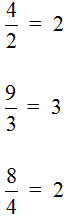 1.5 Измерения в кулинарии Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления. При взвешивании продуктов в кулинарии используются математические величины масса и объём. Ими тоже необходимо уметь пользоваться. Единицы времени играют далеко не последнюю роль в приготовлении блюд. Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика. Вес - можно измерить столовой или чайной ложкой Объём - жидкости можно измерить специальным мерным стаканом Время – все блюда готовятся по времени Температура – каждое блюдо готовится при своей температуре Практическая часть 2.1 Практическая значимость Чтобы ответить на поставленные вопросы, мы поговорили с мамой и выяснили, что для того чтобы пользоваться кулинарными рецептами и производить перерасчёт продуктов по ним, требуется знать, что такое отношение, пропорциональность. В процессе работы мы сталкиваемся с необходимостью определения пропорции неких ингредиентов, которые нам нужны, относительно количества используемой муки. Эта пропорция называется пекарский процент или процент пекаря. Вы наверняка слышали, что выпечка — это точная наука. Чтобы добиться желаемого результата — будь то блины, пышные булочки или торт — вы должны точно отмерять ингредиенты. Один из способов реализовать идеальный рецепт — использовать процентную формулу пекаря- пекарский процент! Что такое пекарский процент?Пекарский процент (также известный как математика пекаря) — это метод определения пропорции ингредиентов при выпечке по отношению к весу муки. Мы можем использовать процент пекаря по многим причинам, в том числе: Для вычисления точных пропорций ингредиентов с одной единицей измерения; Для масштабирование рецептов в большую или меньшую сторону без изменения консистенции теста или кляра; или Для экспериментов с ингредиентами, или для изменений только одного из них, сохраняя процентное содержание других ингредиентов постоянным. Что такое процентная формула пекаря?Теперь вы, вероятно, задаетесь вопросом, как рассчитать формулу пекарского процента. Не волнуйтесь, Формула процента пекаря довольно проста: Процент пекаря = (вес ингредиента / общий вес муки) × 100% Как рассчитать пекарский процент на примере?Чтобы разобрать формулу на примере, т.к. сейчас для всех мусульман наступил священный месяц Рамадан, и все женщины бывают заняты приготовлением блюд на сухур и на ифтар, я тоже никогда не остаюсь в стороне. Т.к. я единственная дочка в семье и у меня еще три брата мне всегда приходится помогать маме по кухне. В каждой семье на сухур готовят курузную лепешку – чурек, т.к. чурек не дает чувствовать голод и легче держать уразу. Для закрепления своей темы эту миссию на сегодня я решила взять на себя. Рецепт чурека: Кукурузная мука 600г., сахар 1ч.л., соль 1 ч.л., сода 1 ч.л., растительное масло 3 ст.л., 2 яйца, кефир 1 л. Важно запомнить, что в пекарских расчетах все считается от муки и мука принимается за 100%. Остальные ингредиенты считаются в процентах от муки. Для приготовления чурека мне нужно: 600г. кукурузной муки = 100% 1л. Кефира примерно 1000г = 166% 1ч.л. соды =10г. = 1.7% 1ч.л. соли=10г = 1.7% 1ч.л. сахара=10г = 1.7% 3 столовые ложки растительного масла=60г =10% 2 яйца=100г=17% Общая масса ингредиентов =1790г.=298.1% Соответственно масса теста равна1790 гр. , а процентное соотношение всех инградиентов равно 298.1%. Как вы видите суммарные доли всех ингредиентов будут больше 100%. В профессиональных рецептах очень часто не указывается состав в граммах, но все инградиенты выражены в процентах и рецептура выглядит так: Кефир = 160% сода = 1.7% соль= 1.7% сахар = 1.7% растительное масло =10% яйца=17% кукурузная мука = 100% Важно запомнить еще один секрет ! – Если разделить вес теста в граммах на суммарный процент инградиентов то вы получите вес муки в граммах. Например в нашем случае вес теста 1790гр. , а суммарный процент инградиентов 298% или 2.98. Делим 1790гр на 2.98 и получаем 600гр муки.   Если наш чурек разделим по диагонали на две равные части, то мы получим две равные доли и тогда каждая доля будет равна ½ или 50%Если же чурек разделить на 4 части, то каждая доля будет равна ¼ чурека или 25% Заключение Изучив тему «Математика в школе. Проценты, дроби, доли в кулинарии», я ответила на вопросы, которые поставила в начале проекта. 1. При приготовлении блюд нужно знать: состав блюда, количество продуктов, их вес, время приготовления, цена продуктов. Всё это связано с математикой. 2. Проценты, дроби и доли в кулинарии нужна для того, чтобы рассчитать количество продуктов и времени для приготовления блюда. А также для расчёта стоимости блюда. Я считаю, что наша работа помогла всем понять, что математика нужна, она может во многом послужить на благо человека. Огромную помощь в этом оказывают учебники по математике, позволяющие взглянуть на предмет с новой, неожиданной точки зрения. Также мы убедились в том, что математические знания процентов, дробей и долей также очень важна в кулинарии, как и в математике. Мои ровесники должны почувствовать это и относиться к математике с большим интересом, увлечением и пониманием необходимости математических знаний, как для будущей их деятельности, так и для жизни человеческого общества. Список литературы 1. Н.М. Мифтахудинова Основы калькуляции и учета на предприятиях общественного питания [Текст] : учеб. / Н. М. Мифтахудинова, Л. М. Богданова . - 2-е изд., перераб. и доп. - М. : Высш. шк., 1989. - 128 с. 2. Сергеев И.Н., Олехник С.Н., Гашков С.В. Примени математику. –М.: Наука. Гл. ред. физ.мат.лит. 1990. – 240с. 3. http://charme.ru – сайт по кулинарии 4.Ткачев М.В. Домашняя математика. М. «Просвещение» .1994. 5. http://www.2000diet.ru/prostie/vipechka/4.php |