оотлт. Научноисследовательская работа по "Математике" учащаяся 8 класса а захарова Е. С
 Скачать 431 Kb. Скачать 431 Kb.
|
|
Муниципальное бюджетное общеобразовательное учреждение «Центр образования № 16» МАТЕМАТИКА В АРХИТЕКТУРЕ Научно-исследовательская работа по "Математике" Выполнил: учащаяся 8 класса А Захарова Е.С. Руководитель: Кузнецова Ольга Алексеевна Тула 2017год Содержание Введение 3 Глава1. Математика в архитектурных чертежах 5 1.1 Как математика помогает добиться прочности сооружений 6 1.2 Геометрические формы в разных архитектурных стилях 9 1.3 Симметрия — царица архитектурного совершенства 10 1.4 Золотое сечение в архитектуре 12 1.5 Число Фидия 17 Глава2. Исследование удобства планировки квартиры 20 2.1 Как же математика может помочь в планировании помещений? 20 2.2 Геометрические формы в различных архитектурных стилях 21 Заключение 26 Список литературы 28 Введение Математика-это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты. Многие математические теории нередко кажутся искусственными, оторванными от реальной жизни, просто непонятными. Если же подойти к этим проблемам с позиции исторического развития, то станет, виден их глубокий жизненный смысл, их необходимость. Поэтому, основополагающий вопрос проекта — «Математика способна решить всё!?» Архитектура — древнейшая сфера человеческой деятельности и ее результат. Главный смысл понятия архитектура состоит в том, что это совокупность зданий и сооружений различного назначения, это пространство, созданное человеком и необходимое для его жизни и деятельности. Тесная связь архитектуры и математики известна давно. Хороший архитектор должен знать аналитическую геометрию и математический анализ, основы высшей алгебры и теории матриц, владеть методами математического моделирования и оптимизации. Порой из-за недостаточного знания математики архитектору приходиться делать немало лишней работы. Проблемный вопрос проекта: можно ли считать математику и архитектуру, существенным и необходимым дополнение одна другой Цель данной работы — проследить влияние математики на архитектуру. Задачи: Найти общие черты математики и архитектуры. Рассмотреть применение математики в архитектурных чертежах, геометрические формы в разных архитектурных стилях. Показать влияние математики на прочность сооружений. Рассмотреть применение принципа симметрии и золотого сечения в архитектуре. 5. Выявить эстетическое влияние математики на архитектуру, рассмотрев зодчество различных эпох, стилей. 6. Рассмотреть архитектуру нашего города. Актуальность Нашего исследования в том, что архитектурные объекты являются неотъемлемой частью нашей жизни. Наше настроение, мироощущение зависят от того, какие здания нас окружают. Назрела необходимость исследования того многообразия объектов, которые появились в нашем городе. Если раньше архитектурные конструкции представляли собой однообразные сооружения, то в настоящее время геометрические формы позволили разнообразить архитектурный облик города. Работа актуальна не только на сегодняшний день. Упорядочению планировки и застройки городов служат регулярная планировка (прямоугольная, радиально-кольцевая, веерная и т.д.), в чём и не обойтись без математики. Математика играет далеко не последнюю роль, а точнее главную. Объектом исследования данной работы является архитектура и математика. Объект Анкетирование, сбор информации, изучение литературы, анализ. Глава1. Математика в архитектурных чертежах. Архитектура – это искусство, это красота. Ведь как сказал Шеллинг «Архитектура – это застывшая музыка в пространстве». Но прежде чем построить такую красоту, мало иметь вдохновение, нужно точно знать где, как и сколько потребуется для строительства пусть даже обычного дома. В своих творениях архитекторы должны совместить функциональность, красоту, гармоничность, комфортность, экономичность и, конечно же, долговечность. В этом им и помогают знания математики. А в чём же всё-таки проявляется эта помощь? Например, для измерения площади земельного участка, архитектору необходимы знания формулы расчета площади и, конечно же, единиц измерения При расчете размеров помещения архитектору необходимо учитывать средний рост человека, приблизительно равный 175 см. Значит, в данном случае он должен знать формулу вычисления среднего арифметического действия. Итак, прежде чем выстроить любое сооружение, нужно предварительно выполнить огромное количество расчетов, измерений. В нашей стране нашло широкое распространение прогрессивный метод строительства по типовым проектам, который наряду с уменьшением объема проектных работ позволяет унифицировать строительные изделия и способствует индустриализации строительства. Примером выполнения и оформления строительных чертежей могут служить чертежи типовых проектов, разрабатываемые ведущими проектными организациями. Объекты, изображаемые на строительных чертежах – всевозможные здания и сооружения, состоят из отдельных частей – конструкций. Примерами конструкций здания могут служить его фундаменты, перекрытия, крыша. При планировке здания руководствуются некоторыми правилами. При перенесении размеров земельного участка и проецировании здания архитектор пользуется признаками подобия фигур, т.е. он не чертит объект в натуральную величину, а пользуется масштабом, стандартное отношение которого 1: 100. Вычерчивание планов начинают с изображения разбивочных или координационных осей, которые определяют расположение стен и колонн в здании. При планировке архитектор пользуется многими теоремами и аксиомами. Например, чтобы отложить несколько последовательно равных отрезков, используется знаменитая теорема Фалеса. Чтобы построить параллельные прямые, архитекторы пользуются рейсшиной. Также построение параллельных прямых выполняют с помощью чертежного угольника и линейки. Этот способ менее востребован, чем предыдущий, но им всё же пользуются, например, при построении малых элементов плана. При проектировании вертикальной планировки используют графоаналитический метод. Графоаналитический метод проектирования вертикальной планировки имеет много разновидностей. Их смысл сводится к тому, что с помощью математики строится аналитическая модель существующего и проектируемого рельефов. Исходным условием является нулевой баланс земляных масс. После того, как все детали, элементы здания поострены, на план наносят все необходимые надписи и размеры. Итак, математические расчеты, измерения, построения – это самые важные и незаменимые методы для архитектора. 1.1 Как математика помогает добиться прочности сооружений. Люди с древних времен, возводя свои жилища, думали, в первую очередь об их прочности. Прочность связана с долговечностью. На возведение зданий люди тратили огромные усилия, а значит были заинтересованы в том, чтобы они простояли как можно дольше. Прочность сооружения обеспечивается не только материалом, из которого оно создано, но и конструкцией, которая используется в качестве основы при его проектировании и строительстве. Прочность сооружения напрямую связана с той геометрической формой, которая является для него базовой. Математик бы сказал, что здесь очень важна геометрическая форма, в которое вписывается сооружение. Самым прочным архитектурным сооружением с давних времен считаются египетские пирамиды. Как известно они имеют форму правильных четырехугольных пирамид. Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет большой площади основания. С другой стороны, форма пирамиды обеспечивает уменьшение массы по мере увеличения высоты над землей. Именно эти два свойства делают пирамиду устойчивой, а значит и прочной в условиях земного тяготения. На смену пирамидам пришла стоечно-балочная система. С точки зрения геометрии она представляет собой многогранник, который получится, если мысленно на два вертикально стоящих прямоугольных параллелепипеда поставить еще один прямоугольный параллелепипед. Это одна из первых конструкций, которая стала использоваться при возведении зданий и представляет собой сооружения, которые состоят из вертикальных стоек и покрывающих их горизонтальных балок. Первым таким сооружением было культовое сооружение — дольмен. Оно состояло из двух вертикально поставленных камней, на которые был поставлен третий вертикальный камень. Нужно заметить, что до сих пор стоечно-балочная конструкция является наиболее распространенной в строительстве. Большинство современных жилых домов в своей основе имеют именно стоечно-балочную конструкцию. Камень плохо работает на изгиб, но хорошо работает на сжатие. Это привело к использованию в архитектуре арок и сводов. Так возникла новая арочно-сводчатая конструкция. С появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей, вошли окружности, круги, сферы и круговые цилиндры. Этот вид конструкции был наиболее популярен в древнеримской архитектуре. Арочно-сводчатая конструкция позволяла древнеримским архитекторам возводить гигантские сооружения из камня. К ним относится знаменитый Колизей или амфитеатр Флавиев. Следующим этапом развития архитектурных конструкций явилась каркасная система. Аркбутаны являлись каркасом, которые окружал сооружение и принимал на себя основные нагрузки. Арочная конструкция послужила прототипом каркасной конструкции, которая сегодня используется в качестве основной при возведении современных сооружений из металла, стекла и бетона. Достаточно вспомнить конструкции известных башен: Эйфелевой башни в Париже и телебашни на Шаболовке. Телебашня на Шаболовке состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов. Причем каждая часть сделана из двух семейств прямолинейных балок. Эта башня построена по проекту замечательного инженера В.Г.Шухова Однополостный гиперболоид — это поверхность, образованная вращением в пространстве гиперболы, расположенной симметрично относительно одной из осей координат в прямоугольной системе координат, вокруг другой оси. Обратите внимание, что любое осевое сечение однополостного гиперболоида будет ограничено двумя гиперболами. Другой интересной для архитекторов геометрической поверхностью оказался гиперболический параболоид. Это поверхность, которая в сечении имеет параболу и гиперболу. Появление новых строительных материалов делает возможным создание тонкого железобетонного каркаса и стен из стекла. Достаточно вспомнить американские небоскребы или, например, здание Кремлевского дворца съездов созданных из стекла и бетона. Именно эти материалы и каркасные конструкции стали преобладающими в архитектурных сооружениях ХХ века. Они обеспечивают зданиям высокую степень прочности. 1.2 Геометрические формы в разных архитектурных стилях. Ни один из видов искусств так тесно не связан с геометрией как архитектура. Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых также строится на базе определенного геометрического тела. Часто геометрические формы являются комбинациями различных геометрических тел Рассмотрим еще один яркий архитектурный стиль — средневековая готика. Готические сооружения были устремлены ввысь, поражали величественностью, главным образом за счет высоты. И в их формах также широко использовались пирамиды и конусы, которые соответствовали общей идее — стремлению вверх. Характерными деталями для готических сооружений являются стрельчатые арки порталов, высокие стрельчатые окна, закрытые цветными витражами. Обратимся к геометрическим формам в современной архитектуре. Во-первых, в архитектурном стиле “Хай Тек”, где вся конструкция открыта для обозрения. Здесь мы можем видеть геометрию линий, которые идуг параллельно или пересекаются, образуя ажурное пространство сооружения. Примером, своеобразной прародительницей этого стиля может служить Эйфелева башня. Во-вторых, современный архитектурный стиль, благодаря возможностям современных материалов, использует причудливые формы, которые воспринимаются нами через их сложные, изогнутые (выпуклые и вогнутые) поверхности. 1.3 Симметрия — царица архитектурного совершенства. Слово симметрия произошло от греч. слова symmetriа — соразмерность. Рассматривая симметрию в архитектуре, нас будет интересовать геометрическая симметрия — симметрия формы как соразмерность частей целого. Замечено, что при выполнении определенных преобразований над геометрическими фигурами, их части, переместившись в новое положение, вновь будут образовывать первоначальную фигуру. При осевой симметрии части, которые, если можно так сказать, взаимно заменяют друг друга, образованы некоторой прямой. Эту прямую принято называть осью симметрии. В пространстве аналогом оси симметрии является плоскость симметрии. Таким образом, в пространстве обычно рассматривается симметрия относительно плоскости симметрии. Этот вид симметрии иногда называют зеркальной. Название это оправдано тем, что обе части фигуры, находящиеся по разные стороны от оси симметрии или плоскости симметрии, похожи на некоторый объект и его отражение в Зеркале Кроме зеркальной симметрии рассматривается центральная или поворотная симметрия. В этом случае переход частей в новое положение и образование исходной фигуры происходит при повороте этой фигуры на определенный угол вокруг точки, которая обычно называется центром поворота. Отсюда и приведенные выше названия указанного вида симметрии. Поворотная симметрия может рассматриваться и в пространстве. Куб при повороте вокруг точки пересечения его диагоналей на угол 90? в плоскости, параллельной любой грани, перейдет в себя. Поэтому можно сказать, что куб является фигурой центрально симметричной или обладающей поворотной симметрией. Еще одним видом симметрии, является переносная симметрия. Этот вид симметрии состоит в том, что части целой формы, организованы таким образом, что каждая следующая повторяет предыдущую и отстоит от нее на определенный интервал в определенном направлении. Этот интервал называют шагом симметрии. Переносная симметрия обычно используется при построении бордюров. В произведениях архитектурного искусства ее можно увидеть в орнаментах или решетках, которые используются для их украшения. Переносная симметрия используется и в интерьерах зданий. Архитектурные сооружения, созданные человеком, в большей своей части симметричны. Они приятны для глаза, их люди считают красивыми. Симметрия воспринимается человеком как проявление закономерности, а значит внутреннего порядка. Внешне этот внутренний порядок воспринимается как красота. Симметричные объекты обладают высокой степенью целесообразности — ведь симметричные предметы обладают большей устойчивостью и равной функциональностью в разных направлениях. Все это привело человека к мысли, что чтобы сооружение было красивым оно должно быть симметричным. Наиболее ярко симметрия проявляется в античных сооружениях Древней Греции, предметах роскоши и орнаментов, украшавших их. С тех пор и до наших дней симметрия в сознании человека стала объективным признаком красоты. Соблюдение симметрии является первым правилом архитектора при проектировании любого сооружения. Если мы мысленно проведем вертикальную линию через шпиль на куполе и вершину фронтона, то увидит, что с двух сторон от нее абсолютно одинаковые части сооружения. Но возможно, что вы не знаете, что в Казанском соборе есть еще одна, если можно так сказать симметрия. Кроме симметрии в архитектуре можно рассматривать антисимметрию и диссимметрию. Антисимметрия это противоположность симметрии, ее отсутствие. Примером антисимметрии в архитектуре является Собор Василия Блаженного в Москве, где симметрия отсутствует полностью в сооружении в целом. Однако, удивительно, что отдельные части этого собора симметричны и это создает его гармонию. Дисимметрия — это частичное отсутствие симметрии, расстройство симметрии, выраженное в наличии одних симметричных свойств и отсутствии других. Примером дисимметрии в архитектурном сооружении может служить Екатерининский дворец в Царском селе под Санкт-Петербургом. Практически в нем полностью выдержаны все свойства симметрии за исключением одной детали. Наличие дворцовой церкви расстраивает симметрию здания в целом. Если же не принимать во внимание эту церковь, то дворец становится симметричным. Завершая, можно констатировать, что красота есть единство симметрии и диссимметрии. 1.4 Золотое сечение в архитектуре. Золотое сечение — гармоническая пропорция, это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему а:Ь=Ь:с или с:Ь=Ь:а. Отрезки золотой пропорции выражаются иррациональной бесконечной дробью 0,618… и 0,382… для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок принять за 100 частей, то большая часть отрезка равна 62, а меньшая —38 частям, В книгах о «ЗОЛОТОМ сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. «Сечение” дает наиболее спокойное соотношение размеров тех или иных длин. Одним из красивейших произведений древнегреческой архитектуры является Парфенон . Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраске, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. другим примером из архитектуры древности является Пантеон. Из многих отношений, которыми издавна пользовался человек при создании гармонических произведений, существует одно, единственное и неповторимое, обладающее уникальными свойствами. Оно отвечает такому делению целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по-разному – «золотой», «божественной». Древнейшие сведения о ней относятся ко времени расцвета античной культуры Приближенно это отношение равно 5/3, точнее 8/5, 13/8 и т. д. Принципы золотого сечения используются в архитектуре и в изобразительных искусствах. Термин «золотое сечение» ввел Леонардо да Винчи. Теперь для полной убедительности и понимания ценности и значения отношения золотого сечения, рассмотрим пропорциональность пирамид Хеопса и Хефрена, где наиболее явно используется этот принцип, т.е. принцип золотого сечения. Нет сомнений в том, что, предпринимая строительство таких гигантов, зодчие очень и очень внимательно рассчитывали все их размеры. Иначе невозможно мыслить организацию этого чрезвычайного по масштабам строительства. Точные соразмерности этих сооружений не вызывают ни малейших сомнений. В книгах о «ЗОЛОТОМ сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. «Сечение” дает наиболее спокойное соотношение размеров тех или иных длин. Одним из красивейших произведений древнегреческой архитектуры является Парфенон . Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным   рис.1 Примеры «золотого сечения» в архитектуре  рис.2 ТРК «Галерея» г.Нальчик  рис.3 Въезд в г. Грозный B настоящее время, в архитектуре, делаются попытки все шире и шире использовать математические методы, но до сих пор, оценка качества произведений искусства, удобными для измерения количественными категориями, оказывается для современной науки непосильной. Золотое сечение – гармоническая пропорция, это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а. Отрезки золотой пропорции выражаются иррациональной бесконечной дробью 0,618… и 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин. Одним из красивейших произведений древнегреческой архитектуры является Парфенон (Vв. До н.э.). Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. Другим примером из архитектуры древности является Пантеон. Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”. Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова. Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания... К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок” 1.5 Число Фидия Не в каждом стиле было описано присутствие геометрических фигур в сооружениях, но тем не менее на нескольких примерах становится совершенно ясно, что без них было бы невозможным что-либо построить. Мы знаем очень много плоских и пространственных фигур, которые иногда называют геометрическими телами. Ни один вообще вид искусств так тесно не связан с математикой, как архитектура. Пятиконечная звезда постоянно привлекала внимание людей своим совершенством. Пифагорейцы – ученики школы Пифагора – выбрали в качестве символа своего союза именно эту звезду. Она же считалась у них амулетом здоровья. И сейчас пятиконечная звезда красуется на флагах и гербах многих стран. В чем же ее привлекательность? Дело в том, что в этой звезде наблюдается удивительное постоянство отношений составляющих ее отрезков. Взгляните на рисунок. Трудно в это поверить, но AD: АС = АС : CD = АВ : ВС = AD :АЕ=АЕ : ЕС. 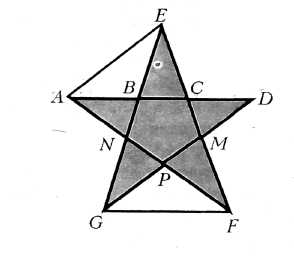 Пользуясь симметрией звезды, этот ряд равенств можно еще очень долго продолжать. А чему же равно это отношение? Чтобы его найти, обозначим AD= а, АС = Ъ и воспользуемся первым равенством. Так как CD= а - b, то из первого равенства отношений следует, что а : b = b: (а - b), или а2 - аb- b2 = 0. Разделив обе части этого уравнения на bи обозначив а/b= Ф, получим уравнение Ф2 - Ф - 1 = 0, откуда Второй корень этого уравнения отрицателен и нас сейчас не интересует. Часто рассматривают не отношение большего отрезка к меньшему, а обратную к нему величину — отношение меньшего отрезка к большему. Число 1/Ф обозначается буквой Ф = 1,618034... и А как разделить отрезок в отношении Ф? Такое построение, производимое циркулем и линейкой, содержится уже в знаменитых «Началах» Евклида, написанных за 300 лет до нашей эры. Процесс построения хорошо виден на рисунке. Сначала к отрезку АВ, который мы хотим разделить в отношении Ф, восставляется перпендикуляр ВС, длина которого равна половине длины отрезка АВ. Затем проводится отрезок АС — гипотенуза треугольника ABC. Далее проводятся две окружности: одна с центром в точке С и радиусом ВС, а вторая с центром в точке А и радиусом AN, где точка N — точка пересечения первой окружности с отрезком АС. Точка М, в которой вторая окружность пересекает отрезок АВ, и будет делить отрезок АВ в отношении Ф, т.е. AM : MB = Ф. 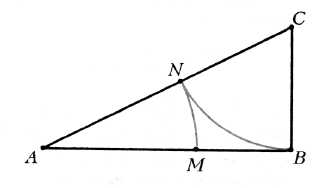 Пропорция, выражаемая числом Ф. по мнению многих исследователей. является наиболее приятной длячеловеческого глаза. Леонардо да Винчи считал, что Идеальные пропорции человеческого тела должны быть связаны с числом Ф. Деление отрезка в отношении Ф он назвал «золотым сечением». В эпоху Возрождения «золотое сечение» было очень популярно среди художников, скульпторов и архитекторов. Размеры картины было принято брать такими, чтобы отношение ширины к высоте равнялось Ф. Этот термин сохранился до наших дней, и само «золотое сечение» по прежнему играет важную роль в искусстве. Им руководствовался, например, великий архитектор Ле Корбюзье. Прямоугольник с таким отношением сторон стали называть «золотым прямоугольником». Форму «золотого сечения» придавали книгам, столам, почтовым открыткам. В дальнейшем книгам и другим бумажным изделиям стали чаще придавать форму прямоугольника с отношением сторон v2. Это связано с тем, что при перегибании такого прямоугольника по средней линии образуются два прямоугольника с тем же соотношением сторон. 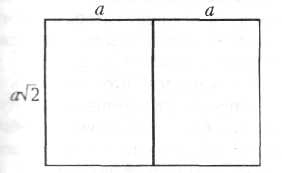 В этом смысле золотой прямоугольник» также обладает интересным свойством: если от него отрезать квадрат, то останется вновь «золотой прямоугольник». Этот процесс можно продолжать до бесконечности . А если провести диагональ первого и второго прямоугольников, то точка О их пересечения принадлежит всем получаемым «золотым прямоугольникам». 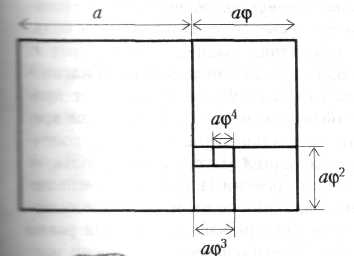 Глава2. Исследование удобства планировки квартиры 2.1 Как же математика может помочь в планировании помещений? Во-первых, при составлении плана чаще всего решается геометрическая задача о разбиении многоугольника на части. Во-вторых, архитектор обязательно пользуется понятием масштаб, т.к. все размеры реальных помещений он уменьшает в какое-либо одинаковое количество раз. Он изображает план с точки зрения математики, представляя его в виде той фигуры, которую можно было бы увидеть, смотря на неё сверху. Далее математика помогает архитектору сделать соответствующие расчёты по известным ему специальным формулам, чтобы решить какой толщины должны быть стены и сколько слоёв звукоизолирующего материала необходимо проложить, чтобы обеспечит жильцам комфортные условия жизни. Удобство для жилых помещений определяется и их планировкой. Понятно, что столовая в доме должна быть недалеко от кухни. Сейчас иногда их объединяют в единое помещение. Туалет и ванная комната должны располагаться рядом, а иногда и просто совмещаться. Наконец, спальня должна находиться рядом с ванной комнатой и туалетом. Детская комната должна быть недалеко от спальни родителей. Вот гостиная, кабинет, библиотека могут располагаться где угодно. Хорошая или плохая звукоизоляция может зависеть от двух основных условий: толщина стен или материал, из которого эти стены сделаны. Сегодня существует много различных звукоизоляционных материалов, которые обеспечивают снижение уровня шума в два и более раз. Математика помогает архитектору сделать соответствующие расчеты по известным ему специальным формулам и ответить на вопрос, какой толщины должны быть стены и сколько слоев звукоизолирующего материала необходимо проложить, чтобы обеспечить жильцам комфортные условия жизни. Толщина стен важна не только для звукоизоляции, она обеспечивает и тепловой режим помещений. Ведь стены защищают людей от неблагоприятного воздействия окружающей среды. И в этом случае для обеспечения хорошей теплоизоляции нужны специальные материалы и расчеты, позволяющие обеспечить защиту от холода и при этом минимизировать затраты на материалы, а значит снизить общую стоимость здания. Теперь же поговорим о планировки жилых зданий, которая является их характеристикой. Рассмотрим это условие на примере той квартиры, где я живу. Теперь поговорим об освещённости. В каждой комнате у нас располагается по одному окну, но достаточно широкому и высокому, что делает помещения светлыми и видимо свободными. Но нельзя ещё забывать архитектору при расположении комнат, что у квартиры есть теневая и солнечная сторона, что тоже немало важно. Толщина стен важна не только для звукоизоляции, она ещё обеспечивает тепловой режим помещений, а это очень важно. Ведь стены защищают людей от неблагоприятного воздействия окружающей среды. Поэтому архитектору в построении чертежа нужно учитывать все, чтобы человеку ничто не доставляло неудобство в планировке его квартиры. 2.2 Геометрические формы в различных архитектурных стилях Давайте проследим, какие стили существовали в различные эпохи и как они менялись. Зодчество. Первым направлением в архитектуре было безусловно, зодчество. Как уже говорилось ранее, все постройки тогда создавались только из дерева, но из-за непрочности этого материала пришлось перейти на более крепкие и более долговечные. Классическая греческая архитектура (около 600-300 до н.э.). В Древней Греции архитектурное решение общественных сооружений было подчинено одной цели – достижению идеальной красоты. Около 600 до н.э. люди начали возводить здания из камня. К 490 до н.э. стали строить из мрамора. Расцвет архитектуры этой эпохи отмечен такими шедеврами, как Парфенон. Храм сооружен из пентелийского белого мрамора, со временем приобретшего теплый желтоватый цвет. Мраморные блоки укладывались насухо и соединялись металлическими вкладышами. Даже кровля покрывалась мраморными пятисантиметровыми плитами - "черепицей". Отличие его заключается в пропорциональном гармоническом строе. Храм по идее прямолинеен, на само же деле в его контурах нет почти ни одной строгой линии. Процесс проектирования, очевидно, заключается в гармонически рассчитанной форме. Древнеримская архитектура (около 200 до н.э. – 400 н.э.). Римские архитекторы заимствовали многие элементы и приёмы у других народов: своды у персов, арки у этрусков, множество архитектурных украшений у греков. Они создавали ряд новых типов архитектурных сооружений – амфитеатры, базилики акведуки; изобрели бетон. Первым отдельно стоящим амфитеатром был Колизей, 70-72 н.э. На примере него можно говорить о применение геометрических форм этого стиля. В основе лежит арочно-сводчатая конструкция, применяются в особенности арки. Также если смотреть чертёж Колизея сверху, то можно увидеть, что его основание построено в форме круга, что ещё раз подтверждает использование в любых архитектурных сооружениях геометрических форм, как сложных, так и простых. Романская архитектура (1000-1100). Этот стиль хронологически следует за византийским (450-600). Для него характерно использование классических элементов, в частности круглых арочных сводов, в зданиях с толстыми стенами. Массивные тяжеловесные стены и колонны служили опорой для кровли, которая первоначально покоилась на цилиндрических, а позднее – на крестовых сводах. Готика (1150-1500). Отличительная черта – стрельчатые арки, позволившие значительно увеличить высоту сводов и окон. Готика распространилась по всей Европе и приобрела типичные узнаваемые черты. Замечательные образцы этого стиля можно видеть в Германии и Великобритании. Вот также несколько примеров этого направления. Смотря на данные иллюстрации можно найти множество геометрических фигур, которые составляют единое целое. Это прежде всего прямоугольники и многоугольники, основа всех сооружений, а если быть точными, то это параллелепипеды и кубы. Далее круги, арки различных видов, конусы и ещё множество фигур, но уже измененных, либо соединенных с другими фигурами. Возрождение (1400-1600). В эпоху Возрождения руины римских сооружений стали источником вдохновения для итальянских архитекторов, создавших художественный стиль, в значительной мере основанный на переосмыслении принципов античности. Снова в центре внимания оказались геометрические пропорции, обилие света и подлинно классически декор. Палладианство (1550-1750). Андреа Палладио несколько упростил стиль Возрождения, сделав акцент на гармоничных пропорциях и симметрии и ограничив количество декоративных элементов. Он первым использовал колоннаду для оформления фасада. Опять же мы видим присутствие геометрических форм, таких как цилиндры, арки, параллелепипеды, просто прямоугольники, треугольники и т.д. Барокко и рококо (1600-1760). Итальянец Бернини создал пышный стиль барокко со сложным оформлением поверхностей и яркими настенными росписями. В XVIII в. Благодаря росту материального благосостояния архитектуры родился более легкомысленный стиль рококо. Причудливые линии и изысканные декоративные формы сочетались с интерьерами, пронизанными воздухом и светом. Неоклассицизм (1750-1850). В пику излишествам и вычурности барокко некоторые европейские архитекторы, например Клод Леду, вновь обратились к античной архитектуре. Новое художественное течение стремилось воссоздать величие классики, используя простую геометрическую планировку и высокие колонны, а также элементы декора, скопированные с греческих и римских образцов. Романтизм/историзм (1800-1900). Интерес к искусству Египта и Азии, к средневековому готическому прошлому породил ряд направлений подражательной архитектуры. Одно из них называется «готическое возрождение», в нём сильны романтические и религиозные мотивы. Характерные особенности – стрельчатые арки, зубчатые стены, сложный декор. Модерн (1890-1914). Стиль модерн охватывает архитектуру, дизайн интерьера, декоративно-прикладное искусство. Его корни следует искать в возрождении интереса к текущим формам кельтского орнамента. Выдающимися образцами модерн стали павильоны станций парижского метрополитена. Ар деко (1918-1940). Для архитектуры этого направления характерны упрощённые конструктивистские формы и повторяющиеся геометрические декоративные элементы. Интернациональный стиль, или функционализм (1920-1975). Функционализм отвергал декоративность и все, кроме функционально необходимого. Сильно его влияние в архитектуре торговых и промышленных зданий. Ле Корбузье сформулировал свои принципы архитектуры: «свободная планировка» интерьера и «свободный фасад» ( расположение окон не зависит от конструкции зданий). Плюрализм (1975). Смешание разнообразных стилей, часто объединённых общим термином «постмодернизм». Школа «хай-тэк» допускает использование старых стилей в новых сочетаниях. Школа «деконструкции» делает акцент на эффекте движения и дезориентации путём зонирования пространства или, наоборот, его расширения с помощью нетрадиционного подхода к таким основным элементам, как пол и стены. Заключение Таким образом, тема проекта актуальна, особенно на нынешнем этапе развития архитектуры. Сложно представить современное градостроительство без математических моделей-прогнозов. Появляются все новые возможности моделирования, основанные на математических расчетах, компьютерные программы, позволяющие архитектору быстрее производить точные измерения, расчеты. Применение ПЭВМ обретало смысл при расчетах каких-либо параметров, создании чертежей, при комбинировании типовых элементов в нормативном проектировании. Возникла возможность создавать модели максимально возможно приближенные к реальности, применяя современные и традиционные разделы математики при увеличении скорости просчета вариантов. Архитектура и математика, являясь соответствующими проявлениями человеческой культуры, на протяжении веков активно влияли друг на друга. Они давали друг другу новые идеи и стимулы, совместно ставили и решали задачи. По сути, каждую из этих дисциплин можно рассматривать существенным и необходимым дополнением другой. Вывод: Математика предлагает архитектору ряд, если так можно назвать, общих правил организации частей в целое, которые помогают: Расположить эти части в пространстве, так, что в них проявлялся порядок; Установить определенное соотношение между размерами частей и задать для изменения размеров (уменьшения или увеличения) определенную единую закономерность, что обеспечивает восприятие целостности и представление о порядке; Выделить определенное место в пространстве, где будет размещаться сооружение, описать его определенной математической формой, которая также позволит выделить его из других сооружений и внести в их состав, создав новую композицию, новый архитектурный ансамбль. Список литературы 1. http://nsportal.ru/ap/library/drugoe/2012/03/29/issledovatelskaya-rabota-matematika-v-arkhitekture 2. Детская энциклопедия. Для среднего и старшего возраста. Д 38 Изд. 2, т. 12. «Искусство». М., «Просвещение», 1968. 3. Савин А., Число Фидия - золотое сечение (Квант N 6,1997), с. 31-32 |
