Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.93 Mb. Скачать 4.93 Mb.
|
|
Усні обчислення Головна мета усного обчислення — засвоєння таблиць арифметичних дій, формування обчислювальних навичок. Вони сприяють також формуванню у дітей вмінь і навичок розв'язувати задачі, розвитку уявлень про математичні поняття, засвоєнню математичної термінології, дають змогу спостерігати деякі математичні закономірності. У ході обчислень пропонують також вправи на розпізнавання геометричних фігур, на порівняння чисел, на знаходження істотної ознаки ряду чисел чи множини фігур та ін. Усні обчислення — специфічна самостійна частина уроку математики (4— 6 хв), але в доборі змісту завдань вона нерідко пов'язується з опитуванням чи підготовкою до сприймання нового матеріалу. Добір завдань для усних обчислень визначається темою уроку, метою закріплення та ліквідації прогалин у знаннях учнів, розвивальною метою навчання математики. Добираючи завдання для усних обчислень, варто використовувати той матеріал підручника, який з тих чи інших причин не застосовувався на попередніх уроках. У разі потреби цей матеріал адаптують до форм проведення усних обчислень. Для усних обчислень можна використати також вправи і задачі, опрацьовані на попередніх уроках: повторно знаходити значення виразів, повторно розв'язувати задачі чи тільки складати плани розв'язування задач; практикувати постановку додаткових запитань до завдань підручника, модифікацію завдань підручника (зміна числових даних, вимоги чи форми проведення). Під час повторного розв'язування задач (2—3 номери, бажано на одному розвороті підручника) учитель відводить час для обдумування (1-2 хв), а потім пропонує повідомити план розв'язування кожної із задач чи саме розв'язання. Як правило, усні обчислення проводяться в швидкому темпі (у цьому допомагають попередні записи та наочність). Проте все це не знімає "навчального моменту" — учитель на якусь мить уповільнює хід роботи, вимагаючи від учнів обгрунтувати відповідь чи пояснити хід розв'язання одного із завдань. Під час усних обчислень застосовуються цікаві форми роботи та елементи змагання. Серед завдань для усних обчислень можна виділити такі: завдання для засвоєння таблиць арифметичних дій; вправи на формування обчислювальних навичок; завдання на засвоєння питань теорії арифметичних дій; задачі; усні вправи з геометрії; завдання з логічним навантаженням. Завдання для засвоєння таблиць арифметичних дій. Після складення кожної таблиці певної арифметичної дії проводиться систематична робота над вивченням її напам'ять. Дітям дають настанову на запам'ятовування. Цей процес відбувається на уроці і вдома. Під час читання таблиць приклади формулюються коротко. Учні опускають слово "дорівнює", для дії додавання вживають сполучник "і", для дії множення — прийменник "на". Наведемо приклади. Розказати таблицю додавання числа 9. (Один і дев'ять — десять; два і дев'ять — одинадцять і т. д.). Розказати таблицю віднімання числа 8. (Дев'ять мінус вісім — один; десять мінус вісім — два і т. д.). Розказати таблицю Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 52 множення числа 5. (П'ять на два — десять; п'ять на три — п'ятнадцять і т. д.). Розказати таблицю ділення на 2. (Чотири поділити на два — два; шість поділити на два — три і т.д.). Такі формулювання легше запам'ятовуються. Для засвоєння і закріплення табличних результатів під час усних обчислень пропонують такі завдання: послідовне (впорядковане) називання всієї таблиці або тільки її результатів; вибіркове називання окремих результатів однієї й тієї самої таблиці чи різних таблиць однієї й тієї самої дії; вибіркове називання результатів таблиць різних дій; обчислення виразів на дві дії на застосування табличних результатів. Вправи на відтворення таблиць подають у більшості з опорою на записи. Це прискорює процес повідомлення. Подамо зразки завдань з опорою на записи. 1. Назвіть таблицю додавання числа 7, користуючись записами: 1 + 7, 2 + 7, 3 + 7, 4 + 7, 5 + 7, 6 + 7, 7 + 7, 8 + 7, 9 + 7. 2. Розкажіть таблицю віднімання числа 8, починаючи з більшого числа.
3. Розкажіть таблицю ділення на 9.
: 9 4. Розкажіть таблиці множення чисел 5 і 6.
5. Назвіть результати зазначених випадків таблиці множення числа 4 і таблиці ділення на 4 (мал. 19). 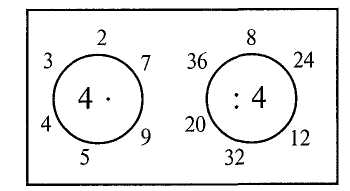 Мал. 19 6. Повідомте результати зазначених дій Методика викладання математики в початкових класах 53  Вправи на формування обчислювальних навичок. У початкових класах формуються навички усних обчислень здебільшого на застосування загальних прийомів. Розрізняють слухову, зорову і зорово-слухову організації усних обчислень. При двох останніх учень, спостерігаючи, в якому порядку і над якими числами треба виконати дії, зосереджує увагу саме на обчисленні та швидкості виконання. Звичайні приклади 1. Назвіть відповіді прикладів у порядку їх запису в рядках. 20-3-6 3-9 + 3 100-3-3 3-8-21 3-2 + 44 3-5-12 38-3-4 38 + 3-7 2. Обчисліть вирази на дві дії і повідомте тільки кінцевий результат. Від числа 50 відняти 15, відняти 7; до числа 17 додати 7, додати 23; 18 плюс 18, мінус 6; 48 мінус 14, плюс 25. Завдання ущільненого характеру До ущільнених (комплексних) завдань належать такі, які забезпечують доволі великий обсяг роботи і дають змогу за допомогою певної наочності чи спеціального добору прикладів швидко організувати навчальну діяльність дітей, лаконічно сформулювати умову; залучити до відповідей багато учнів, підтримувати швидкий темп роботи; сприяти посиленню розумового навантаження школярів. Подамо зразки завдань. 1. Прийом доповнення. Кожне з чисел 5, 8, 20, 23, 37, 40 доповніть до 45. 2. Прийом постановки завдань одного виду: а) кожне з чисел 37, 30, 7, 14, 28, 55 збільшіть на 36; б) до числа 12 додавайте послідовно число 6, поки не отримаєте число 66; в) від числа 90 віднімайте послідовно число 15, поки це буде можливим. 3. Гра "Мовчанка" (мал. 20). 17 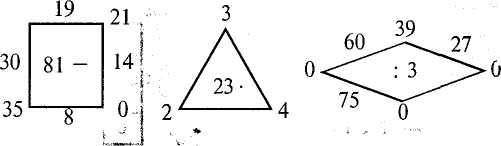 Мал. 20 Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 54 4. Обчислення "ланцюжком". Обчислення "ланцюжком" вчителі проводять в усній формі, називаючи числа і дії. Наприклад: до числа 6 додати 4, відняти 3, відняти 2. Оскільки значна частина дітей класу "губить" числа, то краще застосовувати зорово-слухову форму, спираючись на відповідні записи:
Перший стовпчик читають так: "320 плюс 40, поділити на 4, мінус 20". Ланцюжки можна пропонувати у формі звичайних виразів: (320 + 40): 4 - 20; (300 + 200) • 2 - 400. 5. Обчислювальні таблиці. У таких таблицях римськими цифрами нумерують стовпчики, а великими буквами — рядки. Це дає змогу чітко визначити компоненти дій. Відповіді учні записують або повідомляють усно. Таблиця 9  Зразки завдань (табл. 9): а) додайте числа І і II стовпчиків; б) перемножте числа І і III стовпчиків; в) від чисел IV стовпчика відніміть числа І стовпчика; і: г) числа III стовпчика помножте на 7. Аналогічно виконують завдання з числами, розміщеними в рядках. Якщо дію виконати не можна (на даному етапі навчання), то учні мають про це сказати самі. Наприклад: "Від числа 1 не можна відняти 7, 1 < 7". 6. Структурні записи. За кожним записом скласти й усно розв'язати 12 прикладів на дві дії. 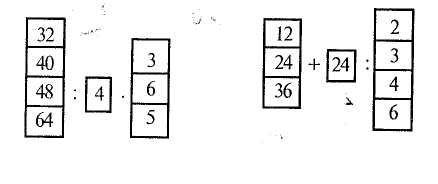 Методика викладання математики в початкових класах 55 7. Постановка комплексних завдань на основі вибірки. Такі завдання часто поєднують усні обчислення з деякими письмовими записами. 1. Знайдіть і запишіть ті приклади, відповіді до яких дорівнюють числам 9,17,20,31. 25-0 81 +9 18-9 40-25 17-9 16 + 4 42 + 6 35-34 29-3 16-8 12 + 5 66 + 6 2. Прочитайте вирази, числове значення яких більше від 25. : 40-13 51-31 25 + 3 44-2 13+13 32-16 43-7 60-3 28-20 16 + 9 14-7 25 + 0 3. Обчисліть значення тих виразів, які є різницями. 3 + 8 (13- 8)+ 4 43-(25+ 4)42: 6 93-6 48 + (16 - 9)(55 + 24) - 83 • 8 4. Усно розв'яжіть рівняння, в яких невідомим є дільник. 34-х = 7 16:х = 8 х-7=17 х:4=16 х-3 = 9 36:х = 4 5. Знайдіть помилки. 65 + ЗО = 68 49 - 7 = 42 70 - 7 = 63 30 + 7 = 100 37 + 3= 40 67-40=27 86 + 3 = 83 24 + 6 = 20 67-20=65 80-4 = 86 88-7 = 81 60-5 = 55 Поясніть, як правильно обчислити вираз 67 — 20. Ігри та ігрові форми завдань До цього виду завдань належать не тільки ігри чи ігрові ситуації, а й завдання з елементами контролю чи змагання. 1. Кругові приклади. їх складають так, щоб перший компонент кожного наступного був результатом попереднього. Результат останнього прикладу дорівнює першому компоненту першого прикладу. Приклади можуть бути як на одну, так і на дві дії. а) 40-13 62-22 13 + 65 90-60 1+61 27-14 78+12 30-29 б) 54 - 54 : 9 72 : 9 • 8 64-2-5 44 + 9-4 80 - 40 : 5 48 - 32 : 8 2. Цікаві квадрати (мал. 21). Заповнення цікавих квадратів не дуже легка справа для усних обчислень, але в шкільній практиці вони використовуються. Тому треба вміти добирати числа, щоб вони утворювали цікавий квадрат. Для цього беруть 9 членів арифметичної прогресії, наприклад, 5, 8, 11, 14, 17, 20, 23, 26, 29. ' 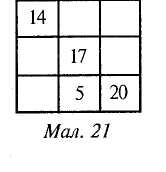 Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 56 Три середніх члени записують по діагоналі квадрата (у нашому прикладі 14, 17, 20), біля найбільшого з них (20) записують найменше число прогресії (5). Це — основа цікавого квадрата. Далі числа квадрата визначають обчисленням: 14 + 17 + 20 = 51 (сума чисел стовпців чи рядків квадрата); 5 + 20 = 25, 51 — 25 = 26. Отже, у нижній порожній клітці треба записати число 26. Наступним обчисленням можна знайти ліве число середнього ряду і т. д. Числа квадрата, що становлять його основу, записує вчитель, а доповнюють учні. Гру краще організувати у вигляді командних завдань між рядами парт. Учителі практикують ігри "Арифметичне лото", "Задумані числа", "Кращий обчислювач", "Естафета", "У кожного своє число". Завдання з термінологічним спрямуванням Молодші школярі засвоюють математичну термінологію шляхом наслідування мови вчителя та в процесі виконання відповідних вправ. Навчальна ефективність таких вправ значно посилюється, якщо їх виконувати з опорою на записи термінів, що вивчаються, на дошці чи на окремих аркушах. Це забезпечує правильне співвіднесення термінів і відповідних математичних понять, дає змогу учням не тільки сприймати терміни на слух, а й самостійно читати їх. Наведемо зразки вправ. 1. Прочитайте завдання і виконайте потрібні обчислення. Відповіді ^повідомляйте усно. Зменшити 32 на 7; 2; 9. Збільшити 8 на 8; 32; 69. На скільки 9 менше від 99; 81; 70? Знайти різницю чисел 85 і 7. Як дізнатися, на скільки одне число менше від іншого? (Навчальний момент). 2. Знайдіть результат дії над кожною парою поданих чисел (табл. 9). 3. Прочитайте приклади по-різному, використовуючи зазначені слова (табл. 10, 11). 4. Обчисліть вирази, в яких від'ємник дорівнює 8. 8+12 63-8 43 + 8 42-(3+ 5) 60 - (8 + 1) 12-8 8-5 50-8 (65 - 8) + 4 60 — (14 — 6) 5. Вправи на закріплення усної і письмової нумерації (в межах 100): Таблиця 9 Таблиця 10
Методика викладання математики в початкових класах 57 Таблиця 11
Назвіть числа, які можна утворити з двох десятків і одноцифрових чисел. Назвіть числа другого десятка, четвертого десятка. Запишіть усі числа сьомого десятка. Назвіть сусідів кожного круглого числа. Для засвоєння таблиць і формування обчислювальних навичок у шкільній практиці застосовуються математичні диктанти. У початкових класах математичні диктанти проводяться на різних етапах уроку. Вони є добрим засобом зворотного зв'язку між учителем і учнями. Виконуючи завдання диктантів, діти стають більш організованими, швидше зосереджуються. Проведення математичних диктантів на етапі усних обчислень сприяє не тільки розвитку навичок обчислення, а й підвищенню їх математичної культури, збагаченню математичної мови. Текст математичних диктантів учитель повинен записати у плані-конспекті уроку. У математичних диктантах учні часто записують не тільки відповіді, а й числові вирази. Проте на етапі усних обчислень вони здебільшого зазначають лише відповіді. Тому результати диктанту слід аналізувати відразу ж після його проведення. На виконання завдань відводиться 1—3 хв. Оскільки арифметичні операції за складністю різні, то диктант треба проаналізувати, щоб паузи були потрібної тривалості. Взагалі бажано визначити провідну тему математичного диктанту (розв'язування задач певного виду; вправ, пов'язаних з математичною термінологією; вправ на застосування певного прийому обчислень та ін.). Подамо зразок математичного диктанту, пов'язаного з математичною термінологією. 1. Знайдіть різницю чисел 92 і 80. 2. Зменшуване 78, від'ємник 70. Знайдіть різницю чисел. 3. Зменшіть число 62 на 11. 4. Від числа 45 відніміть 25. Яке число отримали? 5. Сума двох чисел 84. Другий доданок 41. Знайдіть перший доданок. 6. У змаганнях взяло участь 48 хлопчиків, а дівчаток — на 28 менше. Скільки дівчаток взяло участь у змаганнях? Вправи на засвоєння питань теорії арифметичних дій. Чимало із завдань для усних обчислень можна і треба підпорядковувати засвоєнню властивостей арифметичних дій, зв'язку між результатами і компонентами арифметичних58 Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 58 дій, прийомів послідовного множення і ділення та округлення при додаванні і відніманні. 1. Знайдіть добутки, використовуючи переставляння множників. 25-3-4 7-5-2 2-14-50 2. Знайдіть частки, застосовуючи спосіб послідовного ділення 80:16 256:8 120:15 3. Знайдіть суму, округлюючи один з доданків. 273 + 198 588 + 340 399 + 176 4. Знайдіть різницю, округлюючи зменшуване або від'ємник. 597-140 383-196 647-289 5. Розв'яжіть рівняння на знаходження від'ємника і діленого. х-5 = 25 17-х =8 х + 4=12 44-х =20 х:5=20 20:х=4 х-4=12 42 + х=96 Задачі. У навчанні молодших школярів важливе значення має як письмове, так і усне розв'язування задач. Розв'язуючи задачі письмово, діти краще уявляють план задачі і дії, за допомогою яких вона розв'язується, а тому глибше засвоюють спосіб розв'язування. Проте усно можна більше розв'язати задач. А це важливий фактор у навчанні. Певну роботу над задачами проводять і на етапі усних обчислень. Можна, звичайно, розв'язувати короткі текстові задачі на одну-дві дії, умову яких учні сприймають на слух, але значно краще практикувати такі форми роботи, які спираються на зорові образи. З цією метою використовують таблиці із зображенням предметів (або їх назви) і їх числовими характеристиками (мал. 22). Доцільно розглядати не ізольовані пари предметів, а в сукупності. У цьому разі більш виразна роль запитання для вибору потрібних чисел. 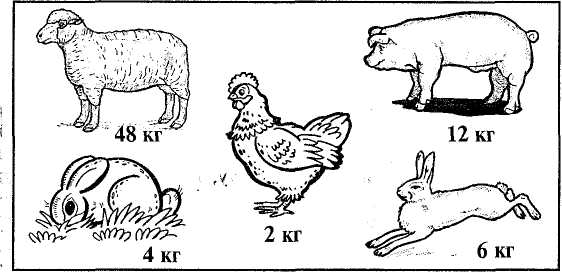 Мал. 22 Запитання: На скільки легша курка від зайця? Курка від вівці? У скільки разів заєць легший від вівці? Кріль від поросяти? На скільки вівця важча від двох зайців? Скільки кілограмів важать вівця і порося разом? Під час усних обчислень широко застосовується усне розв'язування задач з опорою на їх короткий запис. Така опора не потребує багаторазового Методика викладання математики в початкових класах 59 повторення умови, а в деяких випадках учні спроможні сприйняти задачу безпосередньо за малюнком і числовими даними таблиці. Хлопчик наловив окунів і щук. За числовими даними (мал. 23) обчислити, скільки окунів і щук він спіймав разом. 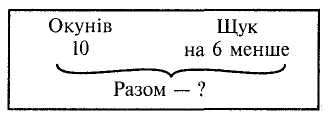 Мал. 23 Усні геометричні вправи. На етапі проведення усних обчислень варто практикувати усні вправи геометричного змісту. Таку роботу бажано проводити хоча б раз на тиждень. Організовують її, як правило, за наперед підготовленими таблицями. Здебільшого геометричні вправи мають комплексний характер. Завдання з логічним навантаженням. Цікаві задачі, завдання підвищеної складності найчастіше практикують на етапі закріплення, але час від часу їх варто використовувати під час усних обчислень. У цьому разі бажано, щоб їх зміст був наближений до теми уроку. Наведемо зразки різновидів задач, які доцільно пропонувати для усних обчислень. Задачі-жарти (Брат з'їв 4 сливи, а сестра — 3. Скільки слив з'їла їхня бабуся?). Задачі, при розв'язуванні яких треба враховувати обставину, не зазначену її тексті ( У сім'ї троє синів. Кожен має сестру. Скільки всього дітей у сім'ї?). Задачі на знаходження всіх можливих відповідей. (1. В ящику було З червоні і 3 зелені палички. Хлопчик узяв 4 палички. Якого кольору вони могли бути? Скільки паличок кожного кольору взяв хлопчик? 2. Назвіть всі двоцифрові числа, які можна утворити за допомогою цифр 2, 5, 9). Знаходження закономірностей або їх "порушників". 1. У кожному рядку знайдіть зайву величину. 23 м 4 см 18 дм 10 кг 5 с 7 год 4 грн. 15 хв 14 т 16 кг 30 км 40 г 2. Яке число в кожному рядку не є результатом таблиць множення? 6 12 18 20 23 30 7 14 21 28 32 37 4 6 8 12 17 24 Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 60 3. У кожному рядку знайдіть зайву фігуру (мал. 24). 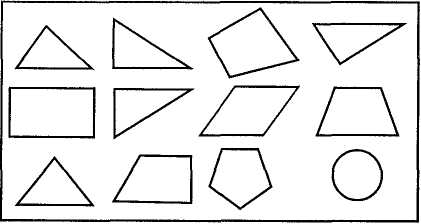 Мал. 24 Головоломки. Застосовуючи знаки дій і дужки, записати числа 2, 3 і 4 трьома трійками. Висловлення. Висловлення або твердження бувають правильними і неправильними. "Усі птахи мають крила" — правильне висловлення, а висловлення "Усі кити вміють літати" — неправильне. Які з поданих тверджень правильні, а які — ні? 1. У кожному прямокутнику протилежні сторони рівні. 2.33 + 57 = 80. 3. 23-8 > 16. 4. Чи завжди правильне твердження, що один з місяців року має 28 днів? |
