№
|
Название
|
Определение
|
Вид
|
Свойства и признаки
|
Особые свойства
|
Формула площади
|
1
|
Параллелограмм
|
четырехугольник, у которого противолежащие стороны попарно параллельны.
|

|
противолежащие стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов, прилежащих к одной стороне, равна 180°;
|
|
S = a*h
|
2
|
Прямоугольник
|
называется параллелограмм, у которого все углы прямые.
|

|
Все свойства параллелограмма (1 - 4)
|
1. диагонали равны
|
S = a*b
|
3
|
Ромб
|
называется параллелограмм, у которого все стороны равны.
|

|
Все свойства параллелограмма (1 - 4)
|
1. диагонали перпендикулярны;
2. диагонали являются биссектрисами его углов.
|
S = a*h
|
4
|
Квадрат
|
называется прямоугольник, у которого все стороны равны.
|

|
Все свойства прямоугольника и ромба
|
|
S = a*a
|
5
|
Трапеция
|
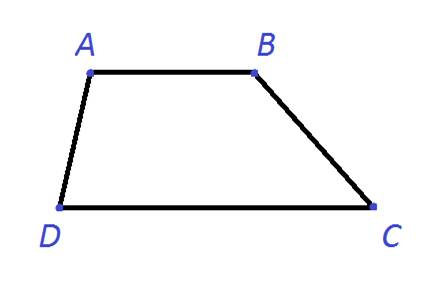
называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называются ее основаниями, а не параллельные стороны — боковыми сторонами.
|
|
Признак: Четырехугольник является трапецией, если его параллельные стороны не равны
|
|
S = 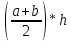
|
5.1
|
Равнобедренная трапеция
|
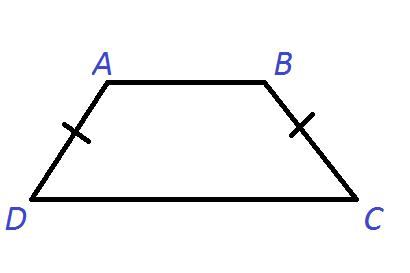
Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.
|
|
1. диагонали равны и углы при основании равны;
|
|
S = 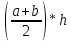
|
5.2
|
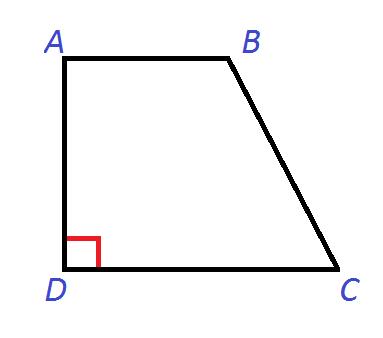
Прямоугольная трапеция
|
Трапеция, один из углов которой прямой.
|
|
|
|
S = 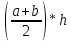
|
 Скачать 12.04 Kb.
Скачать 12.04 Kb.