ллл. Небесное тело. Небесные координаты
 Скачать 138.27 Kb. Скачать 138.27 Kb.
|
|
ГАПОУ Салаватский колледж образования и профессиональных технологий Реферат На тему: Небесное тело. Небесные координаты. Выполнили Студенты 1 И группы Шамова Е.А и Рахматуллина М.Р. г. Салават 2021г. Небесная сфера Небесная сфера — это воображаемая сферическая поверхность произвольного радиуса, в центре которой находится наблюдатель. Небесные тела проектируются на небесную сферу. Из-за малых размеров Земли, в сравнении с расстояниями до звезд, наблюдателей, расположенных в разных местах земной поверхности, можно считать находящимися в центре небесной сферы. В действительности никакой материальной сферы, окружающей Землю, в природе не существует. Небесные тела движутся в беспредельном мировом пространстве на самых различных расстояниях от Земли. Эти расстояния невообразимо велики, наше зрение не в состоянии их оценить, поэтому человеку все небесные тела представляются одинаково удаленными. За год Солнце описывает большой круг на фоне звездного неба. Годичный путь Солнца по небесной сфере называется эклиптикой. Перемещаясь по эклиптике. Солнце в равноденственных точках дважды пересекает небесный экватор. Это бывает 21 марта и 23 сентября. Точка небесной сферы, которая остается неподвижной при суточном движении звезд, условно называется северным полюсом мира. Противоположная точка небесной сферы называется южным полюсом мира. Жители северного полушария его не видят, т. к. он находится под горизонтом. Отвесная линия, проходящая через наблюдателя, пересекает небо над головой в точке зенита и в диаметрально противоположной точке, называемой надиром. Элементы небесной сферы 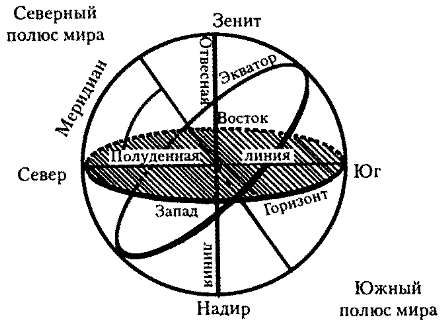 Соотношение между элементами небесной сферы и земного шара 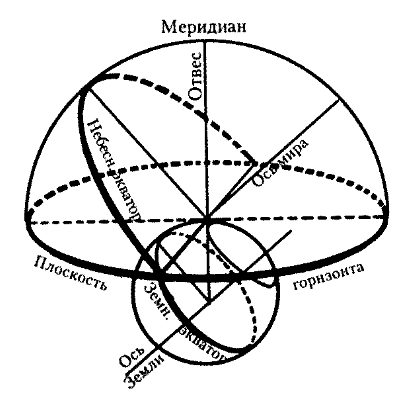 Ось видимого вращения небесной сферы, соединяющую оба полюса мира и проходящую через наблюдателя, называют осью мира. На горизонте под северным полюсом мира лежит точка севера, диаметрально противоположная ей точка — точка юга. Точки востока и запада лежат на линии горизонта и отстоят от точек севера и юга на 90°. Плоскость, проходящая через центр сферы перпендикулярно оси мира, образует плоскость небесного экватора, параллельную плоскости земного экватора. Плоскость небесного меридиана проходит через полюсы мира, точки севера и юга, зенит и надир. История Представление о небесной сфере возникло в глубокой древности; в основу его легло зрительное впечатление о существовании куполообразного небесного свода. Это впечатление связано с тем, что в результате огромной удалённости небесных светил человеческий глаз не в состоянии оценить различия в расстояниях до них, и они представляются одинаково удалёнными. У древних народов это ассоциировалось с наличием реальной сферы, ограничивающей весь мир и несущей на своей поверхности многочисленные звёзды. Таким образом, в их представлении небесная сфера была важнейшим элементом Вселенной. С развитием научных знаний такой взгляд на небесную сферу отпал. Однако заложенная в древности геометрия небесной сферы в результате развития и совершенствования получила современный вид, в котором и используется в астрометрии. Отвесная линия и связанные с ней понятия  Диаграмма, показывающая соотношение зенита, надира и горизонта (в различных определениях). Заметим, что зенит противоположен надиру. Отве́сная ли́ния (или вертика́льная ли́ния) — прямая, проходящая через центр небесной сферы и совпадающая с направлением нити отвеса в месте наблюдения. Отвесная линия пересекается с поверхностью небесной сферы в двух точках — зените над головой наблюдателя и надире под ногами наблюдателя. Истинный (математический, или астрономический) горизонт — большой круг небесной сферы, плоскость которого перпендикулярна к отвесной линии. Истинный горизонт делит поверхность небесной сферы на две полусферы: видимую полусферу с вершиной в зените и невидимую полусферу с вершиной в надире. Истинный горизонт не совпадает с видимым горизонтом вследствие приподнятости точки наблюдения над земной поверхностью, а также по причине искривления лучей света в атмосфере. Круг высоты, или вертикал, светила — большой полукруг небесной сферы, проходящий через светило, зенит и надир. Альмукантара́т (араб. «круг равных высот») — малый круг небесной сферы, плоскость которого параллельна плоскости математического горизонта. Круги высоты и альмукантараты образуют координатную сетку, задающую горизонтальные координаты светила. Суточное вращение небесной сферы и связанные с ним понятия Ось мира — воображаемая линия, проходящая через центр мира, вокруг которой происходит вращение небесной сферы. Ось мира пересекается с поверхностью небесной сферы в двух точках — северном полюсе мира и южном полюсе мира. Вращение небесной сферы происходит против часовой стрелки вокруг северного полюса, если смотреть на небесную сферу изнутри. Небесный экватор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и проходит через центр небесной сферы. Небесный экватор делит небесную сферу на два полушария: северное и южное. Круг склонения светила — большой круг небесной сферы, проходящий через полюсы мира и данное светило. Суточная параллель — малый круг небесной сферы, плоскость которого параллельна плоскости небесного экватора, и следовательно перпендикулярна оси мира. Видимые суточные движения светил совершаются по суточным параллелям. Светила северного небесного полушария движутся вокруг северного полюса мира против часовой стрелки для наблюдателя внутри небесной сферы, а светила южного небесного полушария вокруг южного полюса мира — по часовой стрелке. Круги склонения и суточные параллели образуют на небесной сфере координатную сетку, задающую экваториальные координаты светила. Термины, рождаемые в пересечениях понятий «Отвесная линия» и «Вращение небесной сферы» Небесный экватор пересекается с математическим горизонтом в точке востока и точке запада. Точкой востока называется та, в которой точки вращающейся небесной сферы восходят из-за горизонта. Полукруг высоты, проходящий через точку востока, называется первым вертикалом. Небесный меридиан — большой круг небесной сферы, плоскость которого проходит через отвесную линию и ось мира. Небесный меридиан делит поверхность небесной сферы на два полушария: восточное полушарие и западное полушарие. Полуденная линия — линия пересечения плоскости небесного меридиана и плоскости математического горизонта. Полуденная линия и небесный меридиан пересекают математический горизонт в двух точках: точке севера и точке юга. Точкой севера называется та, которая ближе к северному полюсу мира. Годовое движение Солнца по небесной сфере и связанные с ним понятия 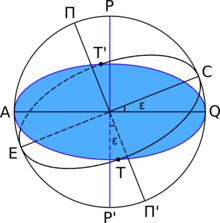 P,P' — полюсы мира, T,T' — точки равноденствия, E,C — точки солнцестояния, П,П' — полюса эклиптики, PP' — ось мира, ПП' — ось эклиптики, ATQT'- небесный экватор, ETCT' — эклиптика Эклиптика — большой круг небесной сферы, по которому происходит видимое годовое движение Солнца. Плоскость эклиптики пересекается с плоскостью небесного экватора под углом ε = 23°26'. Две точки, в которых эклиптика пересекается с небесным экватором, называются точками равноденствия. В точке весеннего равноденствия Солнце в своём годовом движении переходит из южного полушария небесной сферы в северное; в точке осеннего равноденствия — из северного полушария в южное. Прямая, проходящая через эти две точки, называется линией равноденствий[2]. Две точки эклиптики, отстоящие от точек равноденствия на 90° и тем самым максимально удалённые от небесного экватора, называются точками солнцестояния. Точка летнего солнцестояния находится в северном полушарии, точка зимнего солнцестояния — в южном полушарии. Эти четыре точки обозначаются символами зодиака, соответствующими созвездиям, в которых они находились во времена Гиппарха[3] (в результате предварения равноденствий эти точки сместились и ныне находятся в других созвездиях): весеннего равноденствия — знаком Овна (♈), осеннего равноденствия — знаком Весов (♎), зимнего солнцестояния — знаком Козерога (♑), летнего солнцестояния — знаком Рака (♋)[4]. Ось эклиптики — диаметр небесной сферы, перпендикулярный плоскости эклиптики. Ось эклиптики пересекается с поверхностью небесной сферы в двух точках — северном полюсе эклиптики, лежащем в северном полушарии, и южном полюсе эклиптики, лежащем в южном полушарии. Северный полюс эклиптики имеет экваториальные координаты R.A. = 18h00m, Dec = +66°33', и находится в созвездии Дракона, а южный полюс — R.A. = 6h00m, Dec = −66°33' в созвездии Золотой Рыбы. Круг эклиптической широты, или просто круг широты — большой полукруг небесной сферы, проходящий через полюсы эклиптики. Небесные координаты Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли. Системы небесных координат отличаются друг от друга выбором основной плоскости (см. Фундаментальная плоскость) и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальная системы координат. Реже — эклиптическая, галактическая и другие. Система координат, в которой отсчет производится от плоскости экватора, называется экваториальной. Угловое расстояние светила от небесного экватора называется склонением Экваториальные координаты 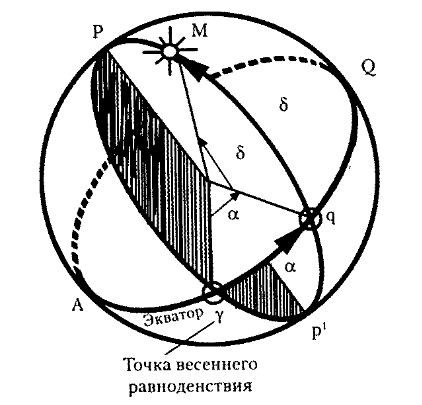 Горизонтальные координаты Угловым расстоянием называется расстояние между объектами на небе, измеряемое углом, который образован лучами, идущими к объекту из точки наблюдения. Угловое расстояние светила от горизонта называют высотой светила над горизонтом. Положение светила относительно сторон горизонта называется азимутом. Отсчет ведется от юга по часовой стрелке. Азимут и высоту светила над горизонтом измеряют теодолитом. В угловых единицах выражают не только расстояния между небесными объектами, но и размеры самих объектов. Угловое расстояние полюса мира от горизонта равно географической широте местности. Высота светил в кульминации Явления Прохождения светил через небесный меридиан называются кульминациями. Нижней кульминацией называется прохождение светил через северную половину небесного меридиана. Явление прохождения светилом южной половины небесного меридиана называется верхней кульминацией. Момент верхней кульминации центра Солнца называется истинным полднем, а момент нижней кульминации — истинной полночью. Промежуток времени между кульминациями — полсуток. У незаходящих светил над горизонтом видны обе кульминации, у восходящих и заходящих нижняя кульминация происходит под горизонтом, ниже точки севера. Каждая звезда кульминирует в данной местности всегда на одной и той же высоте над горизонтом, потому что ее угловое расстояние от полюса мира и от небесного экватора не меняется. Солнце же и Луна меняют высоту, на которой они кульминируют. Первая экваториальная система координат В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t. Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира. Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному. Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с верхней частью небесного меридиана) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу и от 0° до −180° (от 0h до −12h) к востоку. Вторая экваториальная система координат Использование экваториальной системы координат. В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение δ (реже — полярное расстояние p). Другой координатой является прямое восхождение α. Прямым восхождением (RA, α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор, в направлении с юга на север (в весеннее равноденствие). Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу. Объект на небесном экваторе имеет склонение 0° Склонение северного полюса небесной сферы равно +90° Склонение южного −90° У склонения всегда указывается знак, даже если склонение положительно. Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > +90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ < −90° + φ, то объект называется невосходящим, а значит он ненаблюдаем на широте φ.[1] Эклиптическая система координат В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ. Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики. Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть с запада к востоку от точки весеннего равноденствия в пределах от 0° до 360°. Галактическая система координат В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l. Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило. Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу. Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°. Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000). {\displaystyle \delta _{2000}^{C}=-28^{\circ }56',2}История и применение Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат. Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии. Использование различных систем координат[править | править код] Использование горизонтальной топоцентрической системы координат Горизонтальная топоцентрическая система координат используется наблюдателем, находящимся в определённом месте на поверхности земного шара для определения положения какого-либо светила на небе. Координаты небесных светил в данной системе координат могут быть получены с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке. Большинство астрономических компьютерных программ способны выдавать положения светил в данной системе координат. При наблюдениях следует учитывать поправку на рефракцию. Использование первой экваториальной системы координат Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке. Использование второй экваториальной системы координат Вторая экваториальная система координат является общепринятой в астрометрии. В экваториальной гелиобарицентрической системе координат составляются современные звёздные карты и описываются положения светил в каталогах. При этом координаты светил приводятся к определённому положению небесного экватора и точки весеннего равноденствия, то есть к определённой эпохе (в астрономии применяются эпохи B1950 и J2000.0). Экваториальная геоцентрическая система координат отличается от экваториальной гелиобарицентрической системы координат тем, что координаты звёзд скорректированы в ней из-за явления годичного параллакса, а положение небесного экватора и точки весеннего равноденствия приводятся к текущей дате. Использование эклиптической системы координат Эклиптическая геоцентрическая система координат используется в небесной механике для расчёта орбиты Луны, а также является основной или единственной в большинстве школ астрологии. Эклиптическая гелиоцентрическая система координат используется для расчёта орбит планет и других тел Солнечной системы обращающихся вокруг Солнца. Применение различных систем небесных координат На практике, как правило, требуется пользоваться несколькими системами координат. Например для расчёта положения Луны на небе необходимо сначала рассчитать координаты Луны в эклиптической геоцентрической системе координат, пересчитать координаты в экваториальную геоцентрическую систему координат, затем перейти к горизонтальной топоцентрической системе координат. ЗАКЛЮЧЕНИЕ Как правило, мы не задумываемся, откуда взялось деление времени на часы и минуты, и почему самолет, вылетевший из одного аэропорта, спокойно приземляется в другом, а не блуждает беспомощно над землей в поисках места, где можно совершить посадку. Или как корабли находят дорогу в нужный порт, даже когда приходится плыть вдали от суши, и никто не подскажет правильного направления. Оказывается, всему этому мы обязаны астрономии. АСТРОНОМИЯ-это наука о звездах и планетах, о галактике и межпланетном пространстве, о кометах и метеоритах, о космических взрывах и звездных туманностях, в общем, это наука обо всей гигантской Вселенной вокруг нашей планеты и о самой Земле в этой загадочной, непонятной и полной всяких тайн Вселенной. Наша Земля - всего только одно из бесчисленных небесных тел, и даже причина ее возникновения остается предметом особого научного спорта. Жизнь на Земле подчинена тому, что происходит на небе - смене дня и ночи, времен года, полнолуниям и солнечным затмениям. Содержание Небесная сфера Элементы небесной сферы Соотношение между элементами небесной сферы и земного шара История Отвесная линия и связанные с ней понятия Суточное вращение небесной сферы и связанные с ним понятия Термины, рождаемые в пересечениях понятий «Отвесная линия» и «Вращение небесной сферы» Годовое движение Солнца по небесной сфере и связанные с ним понятия Небесные координаты Экваториальные координаты Горизонтальные координаты Высота светил в кульминации Первая экваториальная система координат Вторая экваториальная система координат Эклиптическая система координат Галактическая система координат {\displaystyle \delta _{2000}^{C}=-28^{\circ }56',2}История и применение Использование горизонтальной топоцентрической системы координат Использование первой экваториальной системы координат Использование второй экваториальной системы координат Использование эклиптической системы координат Применение различных систем небесных координат ЗАКЛЮЧЕНИЕ Литература Smart, William Marshall. Text-book on spherical astronomy. — Cambridge University Press, 1949. Lang, Kenneth R. Astrophysical Formulae. — Springer, 1978. — ISBN 3-540-09064-9. Taff, L. G. Computational spherical astronomy. — Wiley, 1980. Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. Fundamental Astronomy. — 2006. — ISBN 978-3-540-34143-7. Roth, G. D. Handbuch für Sternenfreunde. — Springer. — ISBN 3-540-19436-3. Веселовский И. Н. Астрономия орфиков // Вопросы истории естествознания и техники. — М., 1982. — № 2. — С. 120—124. Житомирский С. В. Древность небесных кругов // Земля и Вселенная. — 1998. — № 3. — С. 31—36. Матвиевская Г. П. [www.astro-cabinet.ru/library/Stat/Spherika.htm Сферика и сферическая тригонометрия в древности и на средневековом востоке] // Развитие методов астрономических исследований, Вып. 8. — М.—Л., 1979. Воронцов-Вельяминов Б.А., Е. К. Страут. Астрономия, Базовый уровень, 11 класс. — Дрофа, 2018. — 238 с. . |
