Физика пласта для ЗГД. Нефть стала известна людям более четырёх тысяч лет тому назад

• Название: Нефть стала известна людям более четырёх тысяч лет тому назад
• Анкор: Физика пласта для ЗГД.docx
• Дата: 14.07.2018
• Размер: 459.17 Kb.
• Имя файла: Физика пласта для ЗГД.docx
• Тип: Документы; #21462
• страница: 2 из 8

1 дарси = 1,02×10^-8 см² = 1,02 · 10^-12 м² = 1,02 мкм² ≈ 1 мкм².

 

Проницаемостью в 1 м² называется проницаемость пористой среды при фильтрации через образец площадью 1 м² и длиной 1 м при перепаде давления 1 Па расход жидкости вязкостью 1 Па×с составляет 1 м³/сек.

Пористая среда имеет проницаемость 1 дарси, если при однофазной фильтрации жидкости вязкостью 1 спз (сантипуаз) при ламинарном режиме фильтрации через сечение образца площадью 1 см² и перепаде давления 1 атм., расход жидкости на 1 см длины породы составляет 1 см³/сек.

Физический смысл размерности проницаемости – это величина площади сечения каналов пористой среды, через которые идет фильтрация.

Приведённые выше уравнения (1.5-1.7) справедливы при условии движения несжимаемой жидкости по линейному закону Дарси.

В случае фильтрации газа это условие не выполняется. При перепаде давления объём газа изменяется, и его объем оценивается по закону Бойля-Мариотта:

При Т = const, P·V = const (1.8)

 

Средняя скорость фильтрации газа (V_ср) при линейной фильтрации оценивается:

V_cр· P_ср = V_о ·P_о = V₁· P₁ = V₂ · P₂, (1.9)

 

P_ср = (P₁ + P₂) / 2, (1.10)

 

V_cр = V_о·P_о / P_ср = 2·V_о·P_о / (P₁ + P₂). (1.11)

 

Тогда, средний объёмный расход газа будет равен отношению объема газа (V_ср) за время (t):

. (1.12)

 

Уравнение для оценки коэффициента проницаемости при линейной фильтрации газа запишется с учетом выражений (1.7) и (1.12):

. (1.13)

 

 

1.3.2. РАДИАЛЬНАЯ ФИЛЬТРАЦИЯ НЕФТИ И ГАЗА В ПОРИСТОЙ СРЕДЕ

 

Процесс притока пластовых флюидов из пласта в скважину описывается моделью радиальной фильтрации. В этом случае образец породы представляется в виде цилиндрического кольца с проводящими каналами в осевом направлении (рис. 1.7).

нефтяной пласт

скважина

 

 

 

 

 

Рис. 1.7. Схема радиального притока жидкости в скважину

 

Площадь боковой поверхности цилиндра обозначим через (F) и она оценивается как: F=2prh. Таким образом, уравнение Дарси для радиальной фильтрации нефти (пластовой воды) будет иметь следующий вид:

. (1.14)

 

Отсюда, дебит при радиальной фильтрации жидкости:

. (1.15)

 

 

Таким образом, оценить коэффициент проницаемости при радиальной фильтрации жидкости можно по уравнению (1.16):

. (1.16)

 

 

А для оценки коэффициента проницаемости при радиальной фильтрации газа выражение запишется соответственно с учетом уравнений (1.13) и (1.15).
1.3.3. ОЦЕНКА ПРОНИЦАЕМОСТИ ПЛАСТА, СОСТОЯЩЕГО ИЗ НЕСКОЛЬКИХ ПРОПЛАСТКОВ РАЗЛИЧНОЙ ПРОНИЦАЕМОСТИ

 

Пласт состоит, как правило, из отдельных пропластков, поэтому общая проницаемость пласта (k_пр) оценивается с учетом проницаемости пропластков и направления фильтрации.



 

Рис. 1.8. Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости.

 

При линейной фильтрации жидкости в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости (рис. 1.8), средняя проницаемость пласта рассчитывается следующим образом:

, (1.17)

 

 

где h_i – мощность i-го пропластка; k_i – проницаемость i-го пропластка.

При линейной фильтрации жидкости через пласт, имеющий несколько последовательно расположенных зон различной проницаемости (рис. 1.9),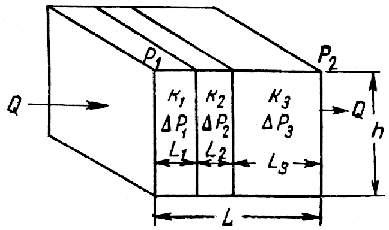

 



 

Рис. 1.9. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости.

 

коэффициент проницаемости пласта рассчитывается следующим образом:

 

, (1.18)

 

 

где L_i – длина i-го пропластка; k_i – проницаемость i-го пропластка.

При радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.10),



Рис. 1.10. Радиальная фильтрация через пласт, имеющий несколько концентрически расположенных зон различной проницаемости.

средняя проницаемость пласта оценивается следующим образом:

(1.19)

 

 

где r_k – радиус контура; r_с – радиус скважины;

r_i – радиус i-го пропластка; k_i – проницаемость i-го пропластка.

 

1.3.4. КЛАССИФИКАЦИЯ ПРОНИЦАЕМЫХ ПОРОД

 

По характеру проницаемости (классификация Теодоровича Г. И.) различают следующие виды коллекторов:

• 
          равномерно проницаемые;
  
• 
          неравномерно проницаемые;
  
• 
          трещиноватые.
  

По величине проницаемости (мкм²) для нефти выделяют 5 классов коллекторов:

1. 
   1.       очень хорошо проницаемые (>1);
   
2. 
   2.       хорошо проницаемые (0,1 – 1);
   
3. 
   3.       средне проницаемые (0,01 – 0,1);
   
4. 
   4.       слабопроницаемые (0,001 – 0,01);
   
5. 
   5.       плохопроницаемые (<0,001).
   

Классификация коллекторов газовых месторождений включает 1–4 классы.

 

1.3.5. ЗАВИСИМОСТЬ ПРОНИЦАЕМОСТИ ОТ ПОРИСТОСТИ

 

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются и более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеальной пористой среды оценивается из соотношений уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:

, (1.20)

 

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давлений.

Коэффициент пористости среды, через которую проходит фильтрация:

. (1.21)

 

Следовательно, уравнение (1.20) можно переписать следующим образом:

 

. (1.22)

 

И сравнить с уравнением Дарси: . (1.23)

 

Приравняв правые части уравнений (1.22) и (1.23) получим выражение для взаимосвязи пористости, проницаемости и радиуса порового канала:

. (1.24)

 

Из чего следует, что размер порового канала можно оценить:

 

. (1.25)

 

Если выразить проницаемость в мкм², то радиус поровых каналов (в мкм) будет рассчитываться:

. (1.26)

 

Уравнения (1.24) – (1.26) характеризуют взаимосвязь между пористостью, проницаемостью и радиусом порового канала. Соотношения (1.24) - (1.26) справедливы только для идеальной пористой среды, например, для кварцевогой песка.

Для реальных коллекторов оценка радиуса порового канала производится с учетом структурных особенностей пород. Обобщенным выражением для этих целей является эмпирическое уравнение Ф.И. Котякова:

, (1.27)

 

где r – радиус пор; j – структурный коэффициент, учитывающий извилистость порового пространства.

Значение j можно оценить путём измерения электрического сопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

. (1.28)

 

Для оценки взаимосвязи коэффициента проницаемости от радиуса порового канала (при фильтрации жидкости только через каналы, капилляры) используются соотношения уравнений Пуазейля и Дарси.

и . (1.29)

 

Причем, пористая среда представляет собой систему трубок. Общая площадь пор через которые происходит фильтрация равна: F = π · r², откуда π = F/ r².

Подставив эту величину в уравнение Пуазейля и сократив одинаковые параметры в выражениях (1.29) получим:

. (1.30)

 

Если r измеряется в [см], а коэффициент проницаемости в [Д] (1Д = 10^-8см). то вводится соответствующий коэффициент пересчета = 9,869·10 ^–9. Тогда, коэффициент проницаемости при фильтрации жидкости через капилляр оценивается эмпирическим выражением:

 

К_пр = r² / (8·9,869·10 ^–9) = 12,5 · 10⁶ r². (1.31)

 

Оценка взаимосвязи коэффициента проницаемости от высоты поровой трещины (для фильтрации жидкости только через трещиноватые поры) оценивается из соотношений уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

, (1.32)

 

где h – высота трещины; v – линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси (1.23) и сократив подобные члены, получим:

. (1.33)

 

С учетом того, что r измеряется в [см], а коэффициент проницаемости в [Д], вводим соответствующий коэффициент пересчета = 9,869·10 ^–9. Тогда, коэффициент проницаемости при фильтрации жидкости через трещину оценивается:

 

К_пр = h² / (12 · 9,869·10 ^–9) = 84,4 · 10⁵ h². (1.34)

 

Уравнения (1.31) и (1.34) используется для теоретической оценки коэффициентов проницаемости для конкретного вида пор. На практике проницаемость породы определяют в лабораторных условиях по керновому материалу (см. раздел лаборат. практикума).

 

1.3.6. ВИДЫ ПРОНИЦАЕМОСТИ

 

Проницаемость абсолютная (физическая) – это проницаемость пористой среды для газа или однородной жидкости при выполнении следующих условиях:

1. 
   1.       Отсутствие физико-химического взаимодействия между пористой средой и этим газом или жидкостью.
   
2. 
   2.       Полное заполнение всех пор среды этим газом или жидкостью.
   

Для продуктивных нефтяных пластов эти условия не выполняются.

Проницаемость фазовая (эффективная) – это проницаемость пористой среды для данного газа или жидкости при одновременном наличии в порах другой фазы (жидкости или газа) или системы (газ-нефть, нефть-вода, вода-газ, газ-нефть-вода).

При фильтрации смесей коэффициент фазовой проницаемости намного меньше абсолютной проницаемости и неодинаков для пласта в целом.

Относительная проницаемость – отношение фазовой проницаемости к абсолютной.

Проницаемость горной породы зависит от степени насыщения породы флюидами, соотношения фаз, физико-химических свойств породы и флюидов.

Фазовая и относительная проницаемости для различных фаз зависят от нефте-, газо- и водонасыщенности порового пространства породы, градиента давления, физико-химических свойств жидкостей и поровых фаз.

Насыщенность – ещё один важный параметр продуктивных пластов, тесно связанный с фазовой проницаемостью: водонасыщенность (S_в), газонасыщенность (S_г), нефтенасыщенность (S_н).

Предполагается, что продуктивные пласты сначала были насыщены водой. Водой были заполнены капилляры, каналы, трещины.

При миграции (аккумуляции) углеводороды, вследствие меньшей плотности, стремятся к верхней части пласта, выдавливая вниз воду. Вода легче всего уходит из трещин и каналов, из капилляров вода плохо уходит в силу капиллярных явлений. Таким образом, в пласте остаётся связанная вода.

Чтобы определить количество углеводородов, содержащихся в продуктивном пласте, необходимо определить насыщенность порового пространства породы водой, нефтью и газом.

Водонасыщенность S_В – отношение объёма открытых пор, заполненных водой к общему объёму пор горной породы. Аналогично определение нефте- и газонасыщенности:

. (1.35)

 

Обычно для нефтяных месторождений остаточная водонасыщенность изменяется в диапазоне: S_В = 6 - 35% (пласт считается созревшим для разработки, если остаточная водонасыщенность в среднем (S_В) < 25%; нефтенасыщенность: S_Н = 65 - 94%, в зависимости от "созревания" пласта.

Для месторождений параметр насыщенности нормирован и равен единице (S_насыщ = 1) или 100%. То есть, для нефтяных месторождений справедливо следующее соотношение:

S_Н + S_В = 1. (1.36)

 

Для газонефтяных месторождений:

 

S_В + S_Н + S_Г = 1, S_г = 1 – (S_B + S_H). (1.37)

 

Остаточная водонасыщенность, обусловленная капиллярными силами, не влияет на основную фильтрацию нефти и газа. На практике насыщенность породы определяют в лабораторных условиях по керновому материалу (см. раздел лаборат. практикума).

Фазовая (эффективная), относительная проницаемости, насыщенность горных пород определяются экспериментально. На рисунке 1.11 представлены результаты экспериментального исследования газо-водо-нефтяного потока при одновременном содержании в пористой среде нефти, воды и газа. Опытами установлено, что в зависимости от объёмного насыщения порового пространства различными компонентами возможно одно-, двух- и трёхфазное движение. Результаты исследования представлены в виде треугольной диаграммы (рис. 1.11).

Вершины треугольника соответствуют стопроцентному насыщению породы одной из фаз; стороны, противолежащие вершинам, – нулевому насыщению породы этой фазой. Кривые, проведённые на диаграмме, ограничивают возможные области одно-, двух-, и трёхфазного потока.

 



Рис. 1.11. Области распространения одно-, двух- и трёхфазного потоков:

1. – 5% воды; 2. – 5% нефти; 3. – 5% газа.

 

При водонасыщенности до 25% нефте- и газонасыщенность пород максимальная: 45-75%, а относительная фазовая проницаемость для воды равна нулю. При увеличении водонасыщенности до 40%, фазовая проницаемость для нефти и газа уменьшается в 2-2,5 раза. При увеличении водонасыщенности до 80% фильтрация газа и нефти в пласте стремится к нулю.

При газонасыщенности меньше 10% и нефтенасыщенности меньше 23% в потоке будет практически одна вода. При газонасыщенности меньше 10% движение газа не будет происходить. При содержании в породе газа свыше 33 –35% фильтроваться будет один газ.

При нефтенасыщенности меньше 23% движение нефти не будет происходить. При содержании воды от 20 до 30% и газа от 10 до 18% фильтроваться может только одна нефть.

Заштрихованные промежуточные области, примыкающие к сторонам треугольника, отвечают двухфазным потокам: газ – вода, газ – нефть, вода – нефть.

Область совместного движения в потоке всех трех фаз выделена двойной штриховкой. Для несцементированных песков она находится в следующих пределах насыщенности: нефтью от 23 до 50%, водой от 33 до 64%, газом от 14 до 30%.