Статистика. 7 проверка стат гипотез. Непараметрические критерии проверки статистических гипотез
 Скачать 30.59 Kb. Скачать 30.59 Kb.
|
Непараметрические критерии проверки статистических гипотез
Так как эти данные выборочные, то для выяснения этого вопроса можно было бы найти средние значения веса и сравнить по критерию Стъюдента. Но, вспомним, что основным условием применения t – критерия является нормальное распределение признака. В нашем случае распределение веса неизвестно и проверить его нельзя из-за ограниченности объема выборки.
Исследуемый признак – возраст - является качественным ординальным, для него нельзя вычислить ни среднее значение, ни дисперсию, нельзя определить распределение. В случае если распределение случайной величины неизвестно, а также если изучаемые признаки являются качественными ординальными, то для проверки гипотезы о принадлежности двух сравниваемых выборок одной генеральной совокупности может применяться и целый ряд непараметрических критериев, среди которых важное место занимают так называемые ранговые критерии. Применение этих критериев основано на ранжировании членов сравниваемых групп. При этом сравниваются не сами члены ранжированного ряда, а их порядковые номера или ранги. Вспомним, что выбор критерия определяется также тем, являются ли сравниваемые выборки зависимыми или независимыми. СЛУЧАЙ 1. Выборки независимы. Весьма распространенным непараметрическим критерием является U-критерий Манна-Уитни. Рассмотрим расчет этого критерия на примере второго проблемного случая. Сформулируем гипотезы: Н(0): Возрастной состав лиц, получающих лечение гемодиализом, не зависит от уровня экономического развития страны Н(1): Возрастной состав лиц, получающих лечение гемодиализом, не одинаков в странах с различным экономическим уровнем (ненаправленная гипотеза) Выберем уровень значимости α=0,01 Вычислим значение U-критерия по следующему алгоритму Объединим все значения обеих выборок в один ранжированный ряд
Каждому элементу этого ряда присвоим ранг, при этом, если несколько элементов ряда совпадают по величине, то каждому присваивается ранг, равный среднему арифметическому их номеров Для каждой выборки находятся суммы рангов R1 = 2,5+5+7+7+10,5+10,5+14=56,5 R2 =2,5+2,5+2,5+7+10,5+10,5+14+14=63,5 Рассчитываются статистики: г 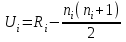 де i=1,2 номера выборок U1 = 56,5 - 7 * 8/2 =28,5 U2= 63,5 -8*9/2 = 27,5 Для проверки правильности расчетов можно использовать следующее соотношение 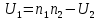 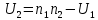 В качестве критерия выбираем наименьшую из двух сумм Uвыч = 27,5 и сравниваем ее с табличным значением для nl =7, n2 = 8 и уровня значимости α=0,01 Uкрит = 6 (Приложение 3, двусторонний тест). Если Uвыч > Uкрит то принимается Н(0) Если Uвыч ≤ Uкрит то принимается Н(1) В нашей задаче вычисленное значение критерия больше табличного, поэтому принимается нулевая гипотеза, и различия в возрастном составе между группами считаются статистически незначимыми (нет аргументов отвергнуть нулевую гипотезу). Но окончательно принять нулевую гипотезу мы пока еще не можем, возможно, мы обнаружим различия, если увеличим объем выборки и применим параметрический критерий. Но этот вопрос относится уже к проблемам планирования эксперимента. СЛУЧАЙ 2. Выборки зависимы.
Исследуемый признак количественный, закон распределения для которого неизвестен и его нельзя оценить вследствие малой выборки, а выборки являются зависимыми (попарно связанными). В таком случае можно использовать непараметрический Т-критерий Уилкоксона. Выдвигаем гипотезы: Н(0): В генеральной совокупности содержание холестерина в плазме крови после приема препарата не изменяется, или «препарат не влияет на содержание холестерина в плазме крови», или «две выборки извлечены из одной генеральной совокупности» Н(1): В генеральной совокупности содержание холестерина в плазме крови после приема препарата изменяется (ненаправленная гипотеза)- Выберем уровень значимости α = 0,05 Т-критерий Уилкоксона вычисляется по следующему алгоритму Вычисляются попарные разницы значений «до» и «после»
Попарные разницы, кроме нулевых, без учета знака ранжируются в один ряд Разницам, кроме нулевых, присваиваются ранги, при чем одинаковым по модулю величинам присваивают одинаковый ранг Отдельно вычисляют сумму рангов положительных (Т+) и отрицательных разностей (Т-), Т+ = 3+3+4+5+6+7=28 Т- = 1+2+3=6 Меньшую из двух таких сумм без учета знака выбирают в качестве критерия: Твыч = 6 Табличное значение для уровня значимости α = 0,05 и числа пар наблюдений п=10 (двусторонний критерий, Приложение 4): Ткрит = 9 Если Твыч > Ткрит то Н(0) Если Твыч ≤ Ткрит то Н(1) В нашем случае вычисленное значение критерия меньше табличного и принимается альтернативная гипотеза. Вывод: Содержание холестерина в плазме крови после приема препарата изменяется с вероятностью не менее 95%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
