тпэфм практические задания. ТПЭФМ_Практическое занятие 1_между лекциями 11 и 12. Непрерывные случайные величины
 Скачать 254.5 Kb. Скачать 254.5 Kb.
|
|
Практическое занятие посвящено решению задач на тему «Непрерывные случайные величины». Случайная величина называется непрерывной (сокращённо НСВ), если множество её значений несчётное, она может принимать любые значения из некоторого промежутка . Примеры непрерывных случайных величин: X − время безотказной работы прибора, Y − расстояние от центра мишени до пробоины при попадании, Z − дальность полёта снаряда и т.д. Закон её распределения задают либо рассмотренной ранее функцией распределения Функция распределения непрерывной случайной величины непрерывна , её график имеет вид:  Плотностью вероятности Вероятностный смысл этой функции заключается в том, что произведение Замечание 1. Для любых случайных величин функция распределения неубывающая, поскольку, по определению, Замечание 2. Плотность вероятности всегда неотрицательна, поскольку это производная от неубывающей функции, т.е. Замечание 3. Можно доказать, что площадь под кривой Замечание 4. Вероятность попадания НСВ в заданный промежуток от Это справедливо, поскольку для произвольного значения  Эта вероятность равна нулю подобно тому, как любая точка на отрезке имеет размер, равный нулю. Следовательно, включение границ в промежуток не влияет на вероятность попадания туда НСВ. Пример 1 . Дана функция распределения 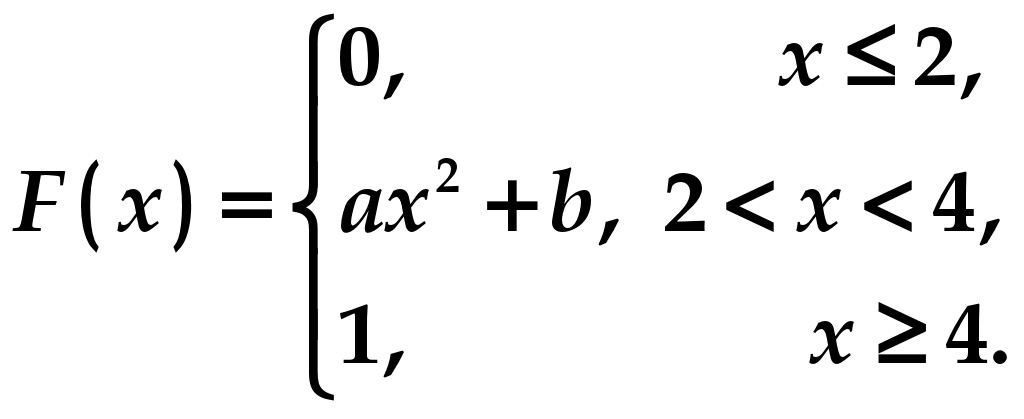 (1) (1)Найти Решение. Параметры 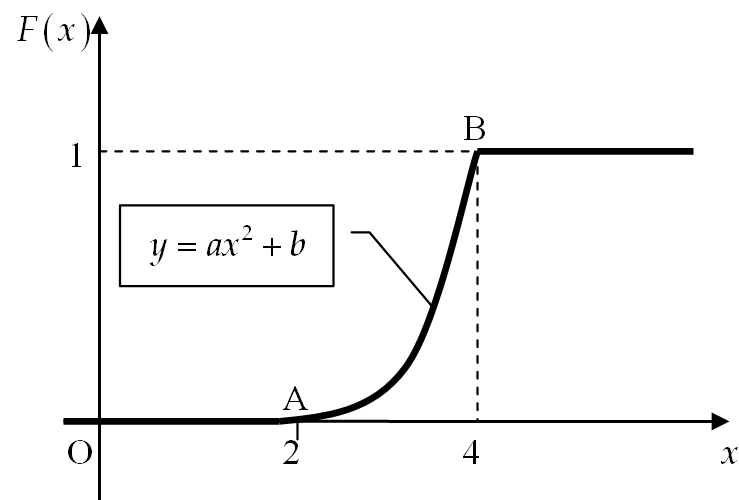 Чтобы кривая 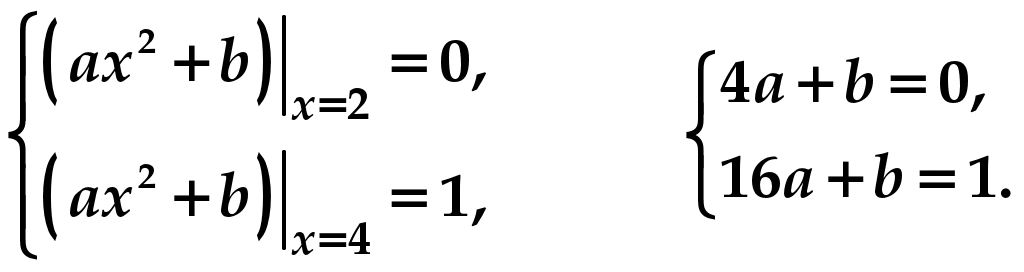 Получим  График плотности вероятности показан на рисунке:  Пример 2. Дана функция распределения 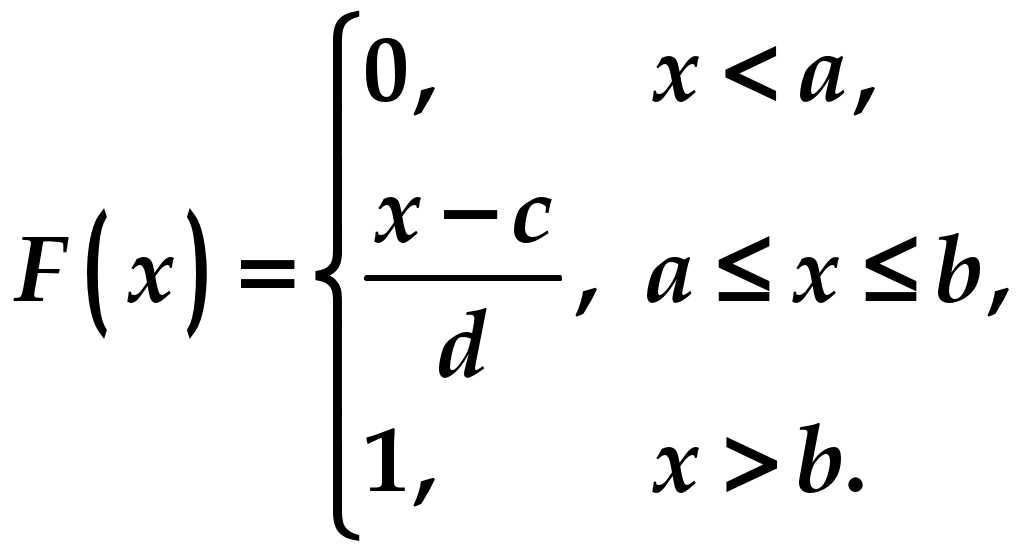 (2) (2)Найти Решение. Параметры 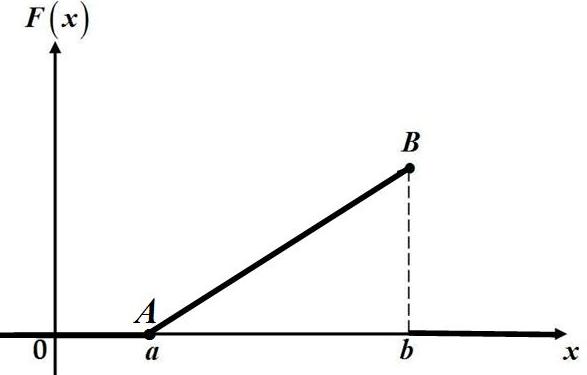 Чтобы прямая  Подставим найденные значения в формулу (1): 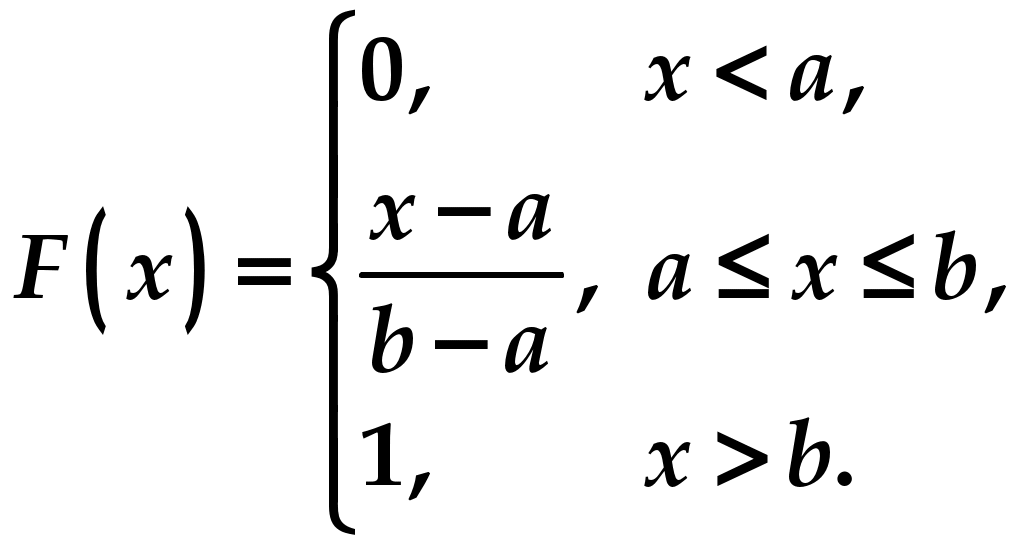 (3) (3)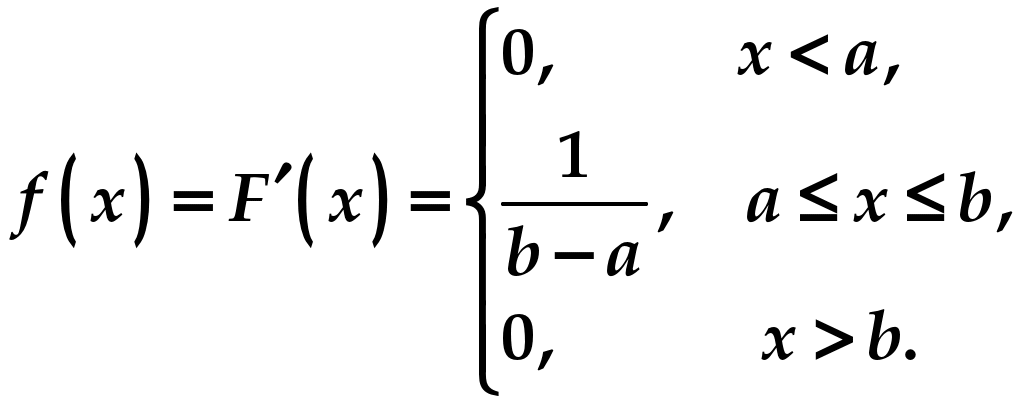 (4) (4)График плотности вероятности показан на рисунке: 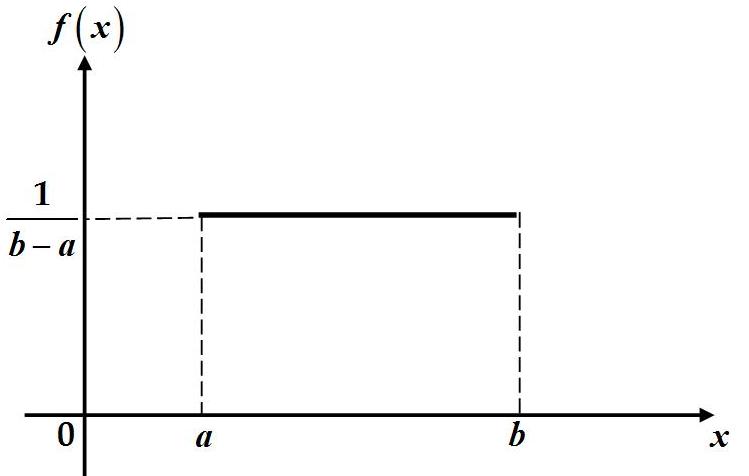 Замечание. Непрерывная случайная величина, закон распределения которой описывается формулами (3) и (4), называется равномерно распределённой на отрезке |
