Несинусоидальные токи и их разложение. Несинусоидальные токи и их разложение
 Скачать 84.45 Kb.
|
|
Несинусоидальные токи и их разложение 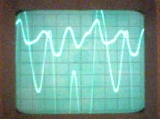 В электрической цепи несинусоидальные токи могут возникнуть по трем причинам: сама электрическая цепь является линейной, но на цепь действует несинусоидальное напряжение, источник напряжения является синусоидальным, но электрическая цепь содержит нелинейные элементы (катушки с магнитопроводом, стабилизаторы напряжения, умножители и делители частоты, магнитные усилители, бареттеры, транзисторы.) старение линейных элементов электрической цепи. Может иметь место также наличие обеих указанных причин. При этом считается, что несинусоидальные напряжения являются периодическими. Генераторы периодических импульсов применяются в различных устройствах радиотехники, автоматики, телемеханики. Форма импульсов может быть различной: пилообразной, ступенчатой, прямоугольной (рис. 1). Генераторы таких напряжений используются в различных устройствах импульсной и вычислительной техники. 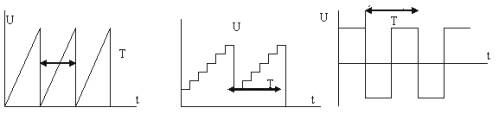 Рисунок 1. 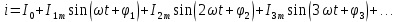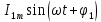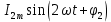Формы импульсов Установлено, что любую периодическую, но несинусоидальную кривую можно приставить как сумму синусоид с разными амплитудами и частотами, кратной одной частоте такая сумма называется тригонометрический ряд Фурье:  Первый член ряда I0 называется постоянной составляющей или нулевой гармоникой, второй член ряда  - основной или первой гармоникой, а все остальные члены вида -при к>1 носят название высших гармоник.Гармоники третьего, пятого, седьмого и д.т. порядков называются нечетными гармониками. Гармоники второго, четвертого, шестого и д.т. порядков называются четными гармониками. I1m, I2m, I3m –амплитуды гармоник. φ1, φ2, φ3 – начальные фазы гармоник. Аналогично для напряжения: 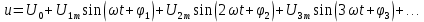 U0-постоянная составляющая, U1m, U2m, U3m –амплитуды гармоник, φ1, φ2, φ3 – начальные фазы гармоник. Такая форма удобна для расчетов несинусоидальных симметричных кривых. Некоторые примеры разложения в ряд приведены в табл. 1, а также они имеются в справочной литературе. 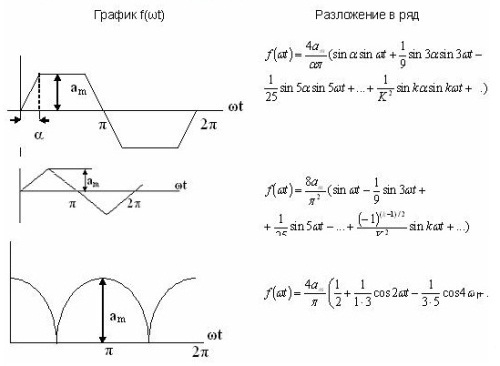 Таблица 1. Разложение в ряд Фурье Свойства периодических кривых, обладающих симметрией Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях. Кривые, симметричные относительно оси абсцисс - если двум ее абсциссам, различающимся на половину периода, соответствуют равные по величине, но противоположные по знаку ординаты. 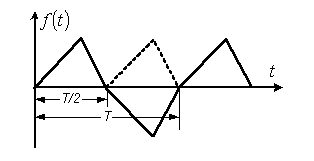 В их разложении отсутствуют постоянная составляющая и четные гармоники. Например: 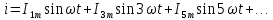 Кривые, симметричные относительно оси ординат – если двум ее равным по величине, но противоположным по знаку абсциссам соответствуют одинаковые по величине и знаку ординаты. 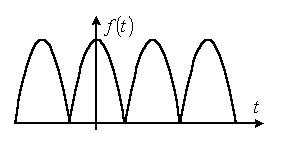 В их разложении отсутствуют синусные составляющие. Например: 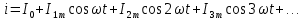 Кривые, симметричные относительно начала координат, если двум любым равным абсциссам с разными знаками соответствуют равные по величине и обратные по знаку ординаты. 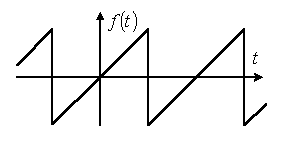 При разложении таких кривых отсутствуют постоянная и косинусные составляющие. Например: 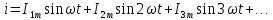 Эти закономерности выполняются и для формулы силы тока, и для напряжения и для ЭДС. |