КАНОНИЧЕСКАЯ ФОРМА ФРОБЕНИУСА ДЛЯ ЛИНЕЙНОГО ОПЕРАТОРА. Фробениусовы канонические формы. Но нас с вами, разумеется, интересует алгебраическая составляющая
 Скачать 66.85 Kb.
|
|
Фробениусовы канонические формы, наряду с параллельными, последовательными и цепными каноническими формами, широко используются в технических приложениях. Название канонические формы получили от вида матриц, введенных в научный обиход берлинским математиком Фердинандом Фробениусом. Фробениусовы канонические формы играют особую роль в установлении взаимосвязи наиболее распространенных типов описания динамических моделей, что нашло, в частности, отражение в пакете математического моделирования «MatLab» и других математических пакетах. Но нас с вами, разумеется, интересует алгебраическая составляющая. В линейной алгебре нормальная форма Фробениуса или рациональная каноническая форма квадратной матрицы A с записями в поле F является канонической формой для матриц, полученных сопряжением обратимых матриц над F. Форма отражает минимальное разложение векторного пространства на подпространства, которые являются циклическими для A (т.Е. охватываются некоторым вектором и его повторяющимися изображениями под A). Поскольку из данной матрицы может быть получена только одна нормальная форма, матрица B подобна A тогда и только тогда, когда она имеет ту же рациональную каноническую форму, что и A. Поскольку эта форма может быть найдена без каких-либо операций, которые могли бы измениться при расширении поля F, в частности, без разложения полиномов на множители, это показывает, что сходство двух матриц не меняется при расширении поля. Форма названа в честь немецкого математика Фердинанда Георга Фробениуса. Что ж, разберём определения: - Пусть дан многочлен ненулевой степени g(x) = a0 + a1x + +a2x 2 + . . . + an−1x n−1 + x n ∈ P[x]. Клеткой Фробениуса, сопровождающей g(x) называется матрица Например, матрицы 1, 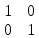 ,  являются клетками Фробениуса, сопровождающие соответственно многочлены: x − 1, x2 − 1, x3- Пусть g1(x), g2(x), . . . , gm(x) – система многочленов, обладающая свойством: gi(x)/gi−1(x) для i = 2, m, причём многочлены gk, k = 1, m ненулевой степени со старшими коэффициентами равными 1, тогда матрица F = diag(F g1, F g2, . . . , F gm) называется матрицей Фробениуса, сопровождающая многочлены g1(x), g2(x), . . . , gm(x). Здесь F gk – клетки Фробениуса (k = 1, m), сопровождающие соответственно многочлены gk, k = 1, m. Если квадратная матрица A ≈ F, то F называется фробениусовой нормальной формой (ФНФ) матрицы A. Перейдём к теоремам, связанным с формой Фробениуса: Теорема 1. Пусть F = diag(F g1, . . . , F gm) – матрица Фробениуса порядка n, сопровождающая многочлены g1(x), g2(x), . . . , gm(x), то система инвариантных множителей матрицы xE − F будет: 1, 1, . . . , 1 {z } n−m , g1(x), g2(x), . . . , gm(x). Также стоит отметить, что Верно утверждение, обратное теореме 1. Теорема 2. Для любой квадратной матрицы А существует единственная фробениусова нормальная форма над полем Р. Для этой теоремы справедливо замечание, что Клетка F g = L T (g), где L(g) – клетка, соответствующая первой естественной нормальной форме: L = diag(L(g1), L(g2), . . . , L(gm)). Метод А.М. Данилевского нахождения канонической формы Фробениуса матрицы Метод основан на подобном преобразовании матрицы. Он относится к числу наиболее быстрых методов. Известно, что подобное преобразование матрицы не изменяет её собственного многочлена. Действительно,  если , то . В качестве матрицы в методе А.М. Данилевского принимается каноническая форма Фробениуса: 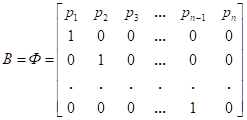 . Коэффициенты первой строки этой матрицы совпадают с коэффициентами собственного многочлена. В этом можно убедиться при помощи разложения определителя по элементам столбцов матрицы : 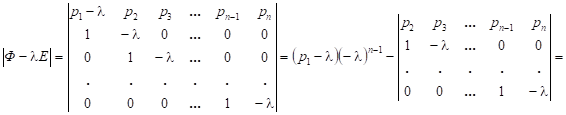 =   . Преобразование исходной матрицы к форме Фробениуса целесообразно проводить последовательными преобразованиями строк и столбцов матрицы. Начнем преобразование с элементов последней строки. Предположим, что элемент последней строки матрицы отличен от нуля. Разделим на него -й столбец матрицы . Тогда последняя строка матрицы примет вид: . Затем будем умножать полученный -й столбец на и вычитать из -го столбца. Проделав это преобразование для , приведем последнюю строку к виду Фробениуса . Можно проверить, что такое преобразование матрицы равносильно умножению её справа на матрицу 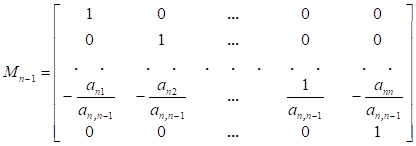 .  Полученная матрица не будет подобна матрице . Чтобы сделать её подобной матрице , нужно умножить слева на матрицу . Такая матрица существует, так как . Можно показать, что 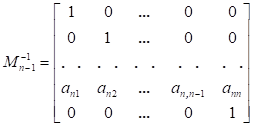 В результате первого шага преобразований получим: 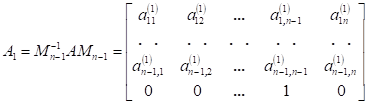 . Второй шаг преобразований аналогичен первому и состоит в приведении предпоследней строки матрицы к виду Фробениуса при условии неизменности последней её строки.  Предположим, что элемент матрицы отличен от нуля. Тогда 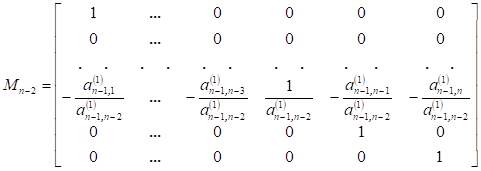 , 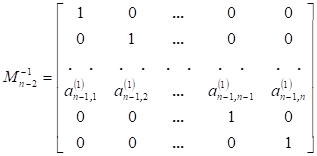 . В результате второго шага преобразований получим 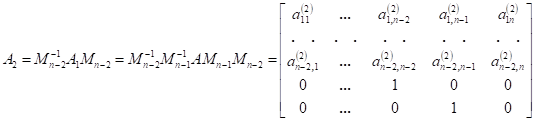  Таким образом, в регулярном случае, когда коэффициенты , , …, , после выполнения шагов изложенных преобразований матрица будет приведена к каноническому виду Фробениуса , (4) где , . Затем по первой строке полученной матрицы составляется искомый собственный многочлен матрицы . |